В газовых смесях возможно протекание химических реакций между различными компонентами. Эти реакции могут быть самыми разнообразными – от горения топлива и взаимодействия среды со стенкой до реакций диссоциации.
Возможность протекания реакций зависит от многих факторов, главными из которых являются температура, давление и скорость потока. Основным критерием, который определяет эту возможность, является число Дамкёлера:
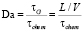 , (1)
, (1)
где τG – характерное газодинамическое время; τchem – характерное время протекания химических реакций; L – характерный размер потока (например, диаметр трубы); V – скорость потока. Как правило, за τchem принимают то время, за которое происходит полное превращение исходных реагентов в продукты реакции.
Наибольшую сложность представляет расчет в случае, когда характерное газодинамическое время сопоставимо со временем протекания химических реакций. Такое течение называется химически неравновесным. Его диапазон, как правило, принимается в пределах примерно: 0,01 < Da < 100. В этом случае необходимо решать уравнения неразрывности всех компонентов газовой смеси и учитывать в них скорости образования этих компонентов в результате всех протекающих химических реакций.
Скорости различных реакций могут существенно отличаться. Например, цепные реакции, как правило, протекают на несколько порядков быстрее, чем реакции диссоциации или рекомбинации. При этом учитывать необходимо и те, и другие реакции. Это порождает серьезную математическую проблему, возникающую при решении системы уравнений неразрывности компонентов, так как эта система является жесткой. Проблема жесткости возникает не только за счет сильного отличия скоростей различных реакций, но и вследствие большой величины критерия Дамкёлера.
Вообще говоря, трудности численного решения подобных систем, получивших название жестких, связаны с выбором шага интегрирования. Дело в том, что характерные времена исследуемых процессов могут различаться в 104–106 раз. Для численного решения системы приходится выбирать шаг по самому быстрому процессу. При этом затраты машинного времени для исследования самых медленных процессов будут неоправданно велики.
По этой причине необходимо искать альтернативные методы для эффективного численного решения рассматриваемых задач.
Основная система уравнений
Для описания течения многокомпонентной химически реагирующей газовой смеси используется система уравнений, которая включает в себя уравнения неразрывности, количества движения, полной энергии и сохранения массы химических компонентов:
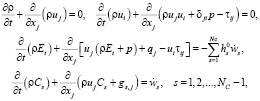 (2)
(2)
где ρ – плотность газовой смеси; ui – компоненты скорости; p – давление; τij – тензор вязких напряжений; Cs – массовая доля компонента s; 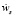 – скорость образования компонента s в результате химических реакций; NC – количество компонентов газовой смеси; gs, j – диффузионная скорость; Et – термодинамическая часть полной энергия; qj – плотность теплового потока, обусловленного теплопроводностью и диффузией;
– скорость образования компонента s в результате химических реакций; NC – количество компонентов газовой смеси; gs, j – диффузионная скорость; Et – термодинамическая часть полной энергия; qj – плотность теплового потока, обусловленного теплопроводностью и диффузией; 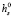 – химическая энергия компонента s.
– химическая энергия компонента s.
Термодинамическая часть полной энергии E отличается от последней тем, что в нее не входит химическая составляющая:
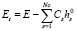 . (3)
. (3)
Численный метод
Практика показывает, что наиболее эффективным для решения системы (2) является полностью связанный численный метод, т.е. одновременное решение всей системы. Кроме того, предпочтительно использовать неявные методы, чтобы избежать строгих ограничений на шаг по времени с точки зрения устойчивости.
1. Векторная форма записи основной системы уравнений. Система (2) в декартовой системе координат может быть представлена в векторной форме:
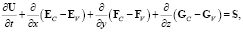 (4)
(4)
где
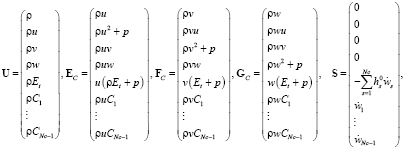 (5)
(5)
 (6)
(6)
В новой криволинейной системе координат (ξ, η, ζ) система (4) примет вид
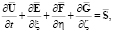 (7)
(7)
где потоки объединены 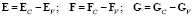 и:
и:
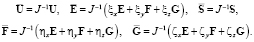 (8)
(8)
Здесь J – якобиан преобразования координат. Конечно-объемное представление уравнения имеет вид
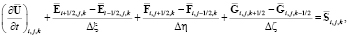 (9)
(9)
где половинные индексы i + 1/2, i – 1/2, j + 1/2 и т.д. означают потоки на соответствующих гранях контрольных объемов.
2. Неявный метод решения системы в случае отсутствия источников. При отсутствии химических реакций 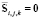 . Неявные численные методы решения системы (9) описаны во многих работах, в частности в работах [1, 2].
. Неявные численные методы решения системы (9) описаны во многих работах, в частности в работах [1, 2].
В работе [1] для представления конвективного потока на гранях использовался метод расщепления Стегера –Уорминга [3], а в монографии [2] – метод Рое [4, 5].
При неявном представлении конвективных и вязких потоков на каждом шаге по времени в каждом узле сетки возникает необходимость многократного обращения матриц Якоби 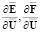 и т.п., а также проведения операций перемножения таких матриц.
и т.п., а также проведения операций перемножения таких матриц.
При отсутствии химических реакций все эти матрицы, а самое главное, матрицы, появляющиеся в промежуточных вычислениях, имеют общий блочный вид:
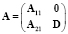 , (10)
, (10)
где матрицы-блоки имеют следующие размеры: A11 – 5х5; A21 – Naх5; D – диагональная матрица размером Na. Здесь Na – число дополнительных уравнений; Na + 5 = Neq – общее число уравнений. Матрица A11 относится к основным уравнениям Навье – Стокса (уравнения неразрывности, количества движения и энергии).
Основные достоинства матрицы вида (10): 1) ее обращение сводится к однократному обращению матрицы A11 и тривиальным операциям перемножения матриц; 2) любые необходимые операции с такой матрицей не меняют ее форму, т.е. блок A12 остается нулевым, а блок A22 остается диагональной матрицей.
Таким образом, даже значительное увеличение числа дополнительных уравнений (т.е. числа химических компонентов) не приводит к существенным затратам компьютерных ресурсов.
Следует сразу отметить, что при наличии ненулевого источника, представленного в неявной форме, оба указанных достоинства исчезают: блок A22 уже не является диагональной матрицей, блок A12 не является нулевым. В этом случае приходится обращать полные матрицы размером NeqхNeq. При большом количестве дополнительных уравнений это может приводить к катастрофическим затратам компьютерных ресурсов.
3. Явно-неявная схема для решения уравнений с жестким источником. В случае, когда основные уравнения обладают ярко выраженной жесткостью, требование устойчивости порождает существенные ограничения на шаг по времени даже при использовании неявного представления источника. Иногда это приводит к тому, что приходится использовать небольшие значения числа Куранта. Таким образом, можно пойти на отказ от неявного представления конвективных и диффузионных потоков, т.е. использовать число Куранта меньше единицы. Источник при этом представляется в неявной форме.
Уравнение (9) можно представить в виде
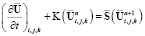 , (11)
, (11)
где 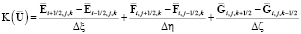 – конечно-объемное представление конвекции и диффузии. Здесь оно представлено в явной форме. Источник представлен в неявной форме. Применяем разложение в ряд Тейлора:
– конечно-объемное представление конвекции и диффузии. Здесь оно представлено в явной форме. Источник представлен в неявной форме. Применяем разложение в ряд Тейлора:
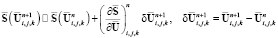 . (12)
. (12)
Тогда из (11) получается
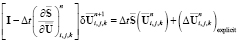 , (13)
, (13)
где 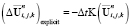 – явное приращение за счет конвекции и диффузии.
– явное приращение за счет конвекции и диффузии.
Предлагаемая явно-неявная численная схема является полностью связанной. При этом в ней нет необходимости многократного обращения на каждом шаге по времени 7-диагональной матрицы. Таким образом, отсутствует наиболее трудоемкая часть решения системы (9), которая появляется при неявном представлении конвекции-диффузии и наличии большого количества дополнительных уравнений.
Серьезным недостатком данной схемы является ограничение на шаг по времени. Для обеспечения сходимости приходится делать большое количество итераций (2000 и более). Причем увеличение числа узлов сетки (т.е. повышение точности расчета) приводит к увеличению числа итераций.
Устранение этого недостатка возможно при использовании схем расщепления, которым посвящен следующий параграф.
4. Явно-неявная схема с чередованием на полушагах. Наиболее простой является схема с расщеплением по физическим процессам. На каждом шаге по времени вместо уравнения (9) решаются последовательно уравнения
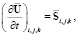 (14)
(14)
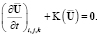 (15)
(15)
При этом на каждом шаге по времени начальным условием для уравнения (15) является решение, полученное в результате решения уравнения (14). Можно поменять эти уравнения местами. Если использовать неявное представление для источника в уравнении (14), а для решения уравнения (15) применить неявный метод, описанный в пп. 2, то в совокупности последовательного решения этих уравнений получается безусловно устойчивый метод.
Недостатки метода расщепления по физическим процессам очевидны: отключение на каждом полушаге взаимодействия различных процессов может приводить к получению нефизичных результатов. Кроме того, возможны проблемы со сходимостью – результаты, полученные после решения уравнения (14), могут несколько отличаться от полученных после решения (15).
Более перспективным является подход, в котором учитываются оба физических процесса, но происходит чередование их явного и неявного представления. Для этого разбиваем текущий шаг по времени Δt на два полушага Δt/2 и решаем систему в два этапа:
Первый полушаг:
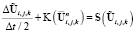 . (16)
. (16)
Второй полушаг:
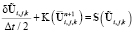 , (17)
, (17)
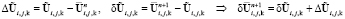 . (18)
. (18)
На первом полушаге 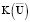 представляется в явной форме, а источник
представляется в явной форме, а источник 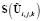 – в неявной. Определяется промежуточное значение вектора
– в неявной. Определяется промежуточное значение вектора 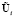 . Затем явное и неявное представления меняются местами, и находится окончательное значение вектора на (n + 1)-ом шаге
. Затем явное и неявное представления меняются местами, и находится окончательное значение вектора на (n + 1)-ом шаге 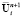 .
.
Можно ввести и более общую форму уравнений на полушагах:
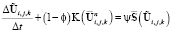 , (19)
, (19)
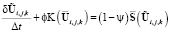 , (20)
, (20)
где на втором полушаге: 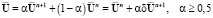 .
.
Здесь α – дополнительный параметр. При α = 1 получается чисто неявная схема; значение α > 1 дает завышенную релаксацию, но это может улучшать сходимость метода.
При ϕ = 1, ψ = 1 из (19), (20) получается схема с расщеплением на физические процессы (уравнения (14), (15)), а при ϕ = 0,5, ψ = 0,5 – схема с полушагами (уравнения (16), (17)).
Уравнение (19) решается так же, как в пп. 3:
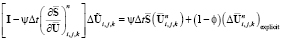 . (21)
. (21)
Вообще говоря, после выполнения первого этапа определяется вектор 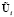 , а по нему – все газодинамические параметры, которые затем используются на втором этапе. Но можно поступить проще и избежать лишних вычислений.
, а по нему – все газодинамические параметры, которые затем используются на втором этапе. Но можно поступить проще и избежать лишних вычислений.
Из (19) следует:
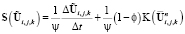 . (22)
. (22)
Подставляя это выражение в (20) и используя формулы (18), получаем
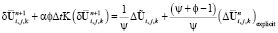 . (23)
. (23)
Здесь использовалась линейность представления конвекции и диффузии:
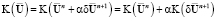 . (24)
. (24)
Это уравнение решается так же, как в пп. 2.
Результаты расчетов
Для апробации численной модели проведен расчет истечения в воздушное пространство сверхзвуковой газовой струи со следующими параметрами на срезе сопла (табл. 1).
Таблица 1
Параметры на срезе сопла
|
pa, Па |
Ta, K |
Ua, м/с |
Ra, м |
XH2 |
XH2O |
XCO |
XCO2 |
XN2 |
|
1х105 |
1330 |
2500 |
1,0 |
0,4 |
0,05 |
0,15 |
0,05 |
0,35 |
Здесь pa, Ta, Ua – соответственно давление, температура и скорость потока на срезе сопла; Xs – мольные доли компонентов; Ra – радиус сопла. Параметры спутного воздушного потока: pe = 0,25х105 Па, Te = 217 K, Ue = 300 м/с.
На рисунке представлены результаты расчета изменения температуры вдоль оси струи при использовании различных численных методов.
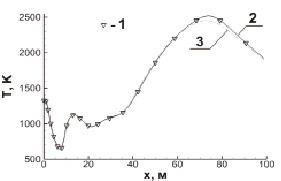
Распределение температуры вдоль оси струи при использовании различных численных схем: 1 – явно-неявная схема (пп. 2.3); 2 – схема с переменой на полушагах (пп. 2.4 ψ = 0,5, ϕ = 0,5); 3 – схема с расщеплением по физическим процессам (ϕ = 1, ψ = 1)
Таблица 2
Сравнение времени расчетов на сетке 120х60
|
Схема |
t, сек |
Схема |
t, сек |
|
Чисто неявная |
350 |
С переменой на полушагах (пп. 4) |
130 |
|
Явно-неявная (пп. 3) |
750 |
С расщеплением по физическим процессам |
270 |
Анализ полученных результатов показывает наибольшую эффективность схемы с переменой на полушагах (пп. 4 ψ = 0,5, ϕ = 0,5); результаты расчета в точности совпадают расчетами, полученными на чисто неявной схеме (на рисунке не приведена) и на явно-неявной схеме, а время расчета существенно меньше. Для схемы с расщеплением вообще не удалось получить результат с удовлетворительной сходимостью.



