В современном мире водные ресурсы представляют высокую ценность и испытывают значительное антропогенное воздействие [1]. С другой стороны, водоемы являются объектами повышенной опасности, так как могут являться источником таких опасных явлений, как наводнения. В условиях быстро развивающегося опасного явления необходимо уметь оперативно прогнозировать возможные сценарии развития событий и принимать на их основе упреждающие решения, что позволит спасти человеческие жизни и сократить материальный ущерб. Таким образом, система мониторинга и прогнозирования гидродинамики мелководного водоема является важным компонентом системы безопасности в прибрежных регионах [2].
Одной из отличительных особенностей мелководного водоема можно назвать близкое расположение горизонтальных границ, в связи с этим неточности аппроксимации границы вносят больший вклад в итоговый результат моделирования, нежели при работе с глубоководными водоемами. По этой причине ставится задача построения математической модели гидродинамики мелководного водоема с уточненными граничными условиями для прогнозирования затопления прибрежных районов [3].
Формулировка непрерывной модели
В модель входят [4]:
Уравнения движения Навье – Стокса в векторном виде:
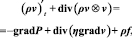 (1)
(1)
уравнение неразрывности:
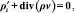 (2)
(2)
уравнение, описывающее эволюцию функции заполненности:
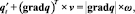 (3)
(3)
где ρ – функция плотности жидкости, v – вектор скорости движения среды, η – тензор динамической вязкости, μ – тензор кинематической вязкости, P – давление, f = κ + g – источник, где g – вектор ускорения свободного падения, а κ – сила Кориолиса, q – функция заполненности, ω – скорость испарения жидкости.
Постановка граничных условий
Граничные условия должны согласовываться с уравнением модели и, таким образом, учитывать физику протекающего процесса, а также учитывать физические свойства самой границы [5].
Пусть граница расчетной области представима в виде
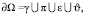
где γ – твердая непроницаемая неподвижная граница (дно водоема), π – свободная подвижная граница (свободная поверхность), ε – фиксированный вход (сечения русел втекающих рек), ϑ – свободный выход.
Отсутствие потока жидкости через непроницаемую границу γ запишем в виде
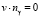 , (4)
, (4)
где nγ – нормаль к данной границе. Чтобы получить граничное условие, удовлетворяющее (4), запишем уравнение (1) на границе области и умножим его на нормаль к этой границе. После преобразования получим граничное условие для давления:
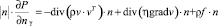 . (5)
. (5)
Если в начальный момент времени выполняется условие (4), то условие (5) гарантирует выполнение (4) в любой другой момент времени.
В качестве граничного условия для скорости примем условие скольжения с трением:
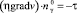 , (6)
, (6)
где τ – тензор касательных напряжений, вызванных трением сплошной среды о границу области.
Граничное условие для давления на поверхности жидкости (свободной подвижной границе π) часто берется в виде равенства давления на поверхности жидкости атмосферному:
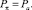 (7)
(7)
В качестве недостатка такого вида граничного условия стоит отметить, что при расчете давления предполагается точное знание формы свободной поверхности.
Сформулируем другой вариант граничного условия для свободной поверхности, скалярно умножив уравнение (1) на нормаль к поверхности с преобразованием производной по времени:
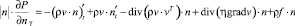 .
.
Учитывая, что 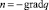 и уравнение (3):
и уравнение (3):
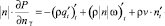
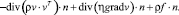 (8)
(8)
Форму свободной поверхности будем искать, используя условие (7) и функцию заполненности:
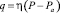 , (9)
, (9)
при этом на характер течения накладывается ограничение вида 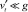 , где g – ускорение свободного падения.
, где g – ускорение свободного падения.
Таким образом, условия (7)–(8) будут выполняться для свободной поверхности.
Можно показать, что если в начальный момент времени выполняется уравнение (3), то граничное условие (8) гарантирует выполнение уравнения (3) в произвольный момент времени.
Фиксированный поток ε не зависит от установившегося в расчетной области гидрологического режима.
Пусть на границе задано фиксированное значение скорости
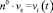 (10)
(10)
и отсутствует трение о границу:
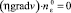 . (11)
. (11)
Как и ранее, граничное условие для давления получим, спроецировав уравнения Навье – Стокса на нормаль к границе:
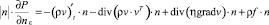 .
.
Учитывая (10), получим граничное условие для давления:
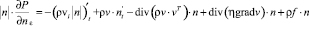 . (12)
. (12)
Граничное условие (12) можно использовать для описания движущейся стенки, например, из-за осаждения взвешенных частиц в жидкости, при этом vi – нормальная составляющая скорости движения границы. Если граница неподвижна, то 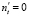 .
.
Если в нулевой момент времени справедливо (10), то условие (12) для системы уравнений гидродинамики гарантирует выполнение (10) в любой момент времени.
При построении граничного условия на границе «свободный выход» ϑ предположим, что значение скорости зависит от гидрологического режима водоема, то есть не является фиксированным, и трение отсутствует:
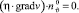 (13)
(13)
Структура течений во внешнем водоеме неизвестна, поэтому требуется построить приближенную модель для описания давления. Предположим, что на отдалении l от границы «свободный выход» во внешнем водоеме давление приближенно равно гидростатическому, а изменение давления при отдалении от границы можно считать линейным, плотность среды равна плотности вблизи границы. Учитывая эти предположения, производную вдоль нормали к границе можно записать в виде
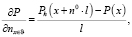
где Ph – гидростатическое давление, определяемое по формуле (ось Oz направлена в сторону ускорения свободного падения):
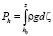 .
.
Тогда условие на границе приближенно запишется в виде
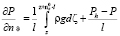 . (14)
. (14)
Считая l достаточно малым, (14) можно приближенно переписать в виде
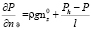 . (15)
. (15)
Тензор касательных напряжений τ определяется согласно закону Ван-Дорна:
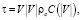 (16)
(16)
где ρc – плотность среды, которая трется о жидкость, V – относительная скорость среды, 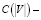 безразмерный коэффициент.
безразмерный коэффициент.
В случае твердых границ области ρc = ρv, V = –ν, где ρv – плотность взвеси. На поверхности ρc = ρa, V = W – ν, где ρa – плотность атмосферы, W – скорость ветра.
Безразмерный коэффициент задается формулой
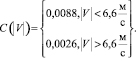
Расщепление непрерывной модели по физическим процессам
При решении задачи гидродинамики (1)–(3) особой сложностью является нахождение поля давления, которое входит в уравнение (1), в то время как компоненты поля скоростей входят во все уравнения (1)–(3). Одним из способов решения данной проблемы является использование метода поправки к давлению [6, 7].
Поле скоростей ищем в два этапа. Рассмотрим вспомогательное поле скоростей  , которое может не удовлетворять уравнению неразрывности:
, которое может не удовлетворять уравнению неразрывности:
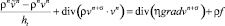 . (17)
. (17)
Требуемое поле скоростей ν найдем из уравнения неразрывности, используя поле скоростей  и поле давления:
и поле давления:
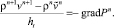 (18)
(18)
Рассчитываем поле давления так, чтобы полученное поле скорости удовлетворяло уравнению неразрывности:
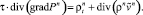 (19)
(19)
Граничные условия строятся, исходя из физических свойств границы, уравнений (17) – (19), и согласуются с граничными условиями непрерывной модели.
Граничное условие для свободной границы примет вид
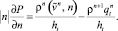 (20)
(20)
Граничное условие для непроницаемой границы получаем из (20), полагая границу области постоянной (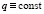 ).
).
Дискретизация уравнений модели
Аппроксимацию уравнений модели по времени проводим методом поправки к давлению. Для более точной аппроксимации границы дискретизация пространственных производных выполняется интегро-интерполяционным методом с учетом частичной заполненности ячеек расчетной сетки.
Аппроксимация конвективных и диффузионных слагаемых имеет вид:
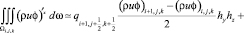
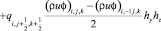 , (21)
, (21)
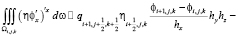
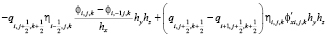 , (22)
, (22)
где 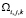 – ячейка расчетной сетки.
– ячейка расчетной сетки.
Модель консервативна, дискретная модель имеет второй порядок погрешности аппроксимации по пространству во внутренних узлах и первый порядок в приграничных узлах. При использовании интегро-интерполяционного метода без учета частичной заполненности ячеек расчетной сетки в приграничных узлах получается нулевой порядок погрешности аппроксимации, то есть допускается константная ошибка. Условия устойчивости модели имеют вид
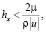
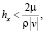
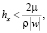
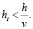
Численные эксперименты
Проверка правильности результатов, полученных в ходе программной реализации описанной выше дискретной модели, осуществлялась на модельных задачах:
1. Резервуар с фиксированным источником и свободным выходом.
При моделировании первой задачи в векторном поле скорости по обе стороны от основного потока наблюдается образование вихрей, что согласуется с физикой процесса. Кроме того, получено, что поток через непроницаемые границы области равен нулю и масса втекающей жидкости равна массе вытекающей (с точностью 10-9), что означает выполнение закона сохранения массы.
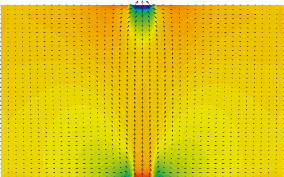
Рис. 1. Результаты моделирования течения жидкости в резервуаре с фиксированным источником и свободным выходом. Горизонтальное сечение. Векторное поле соответствует функции скорости, а поле давления показано цветом. Для наглядности вектора скорости были масштабированы
|
|
|
|
а) Моделирование без учета частичной заполненности ячеек расчетной сетки |
б) Моделирование с учетом частичной заполненности ячеек расчетной сетки |
|
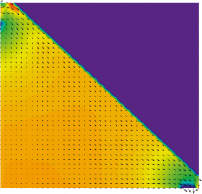
Рис. 2. Результаты моделирования течения жидкости в скошенном резервуаре (векторное поле – поле скорости, цветом показано поле давления) |
|
2. Течение в резервуаре со скошенной стенкой.
При моделировании второй задачи без учета частичной заполненности ячеек расчетной сетки скошенная стенка заменяется на ступенчатую, что приводит к падению скорости течения вдоль стенки (рис. 2, а). При моделировании течения в скошенном резервуаре с использованием метода конечных объемов с учетом частичной заполненности ячеек расчетной сетки (рис. 2, б) этого эффекта удается избежать.
Проверка на модельных задачах не может полностью гарантировать правильность построенной модели, но обеспечивает проверку соответствия получаемых результатов физике реально протекающего процесса.
Выводы
В работе построена математическая модель гидродинамики и сгонно-нагонных явлений в мелководных водоемах на основе пространственно-трехмерных уравнений Навье – Стокса с постановкой уточненных граничных условий. Уточненные граничные условия построены на основе исходных уравнений модели и физических ограничений, налагаемых свойствами границы. Разработана модель описания движения свободной поверхности, не требующая решения уравнения переноса на каждом временном шаге. Для аппроксимации уравнения на пространственной сетке используется интегро-интерполяционный метод с частичной заполненностью ячеек расчетной сетки. Применение перечисленных методов позволило построить алгоритм моделирования гидродинамики мелководного водоема со свободной поверхностью и изменяемой береговой линией на основе статических регулярных сеток, а также добиться большей точности моделирования по сравнению с классическими методами расчета на регулярных сетках. Использование статических регулярных сеток позволяет избежать дополнительных временных расходов на перестроение сетки, повысить эффективность программной реализации, а также упростить параллельный алгоритм расчета модели.
Работа выполнена при финансовой поддержке РФФИ по проекту № 15-07-08408.