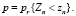В условиях суммирования случайного числа случайных величин вычисление интеграла по формуле обращения в некоторых случаях затруднительно. Очевидно, объективно существует потребность разработки специфических методов и соответствующего аналитического аппарата, основной целью которых должно быть обеспечение исследования поведения сумм случайного числа св. (нахождение их функций распределений, функций квантилей и моделирующих алгоритмов). В качестве возможного пути преодоления трудностей решения этих задач далее рассматривается применение одного класса операторных рядов (рядов С. Ли).
Итак, воспользуемся основными математическими понятиями и определениями. В традиционном понимании следующая последовательность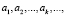 
записанная в виде суммы, именуется рядом, где ak (k = 1,…,n), которые называются членами ряда, обычно являются числами, функциями, векторами, матрицами. Обычно мы имеем дело с числовыми, функциональными рядами, а также с рядами векторов, матриц и т.д. В данной работе применяется совершенно другой класс рядов, элементами которых являются операторы. Соответственно, такие ряды называются операторными. Известно, что под оператором понимают отображение X > Y, ставящее в соответствие каждому элементу x из множества X некоторый элемент y из Y. Пример подобных преобразований – дифференцирование: любой функции f(x), имеющей производную, ставится в соответствие оператором дифференцирования функция 
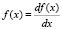. Рассмотрим линейные дифференциальные операторы следующего вида:
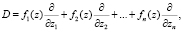(1)
где fi(z) – коэффициенты, являющиеся функциями комплексных переменных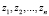 
. Допустим, что все эти коэффициенты в окрестности некоторой точки z0 голоморфны, а значит fi(z) – однозначные аналитические функции. Известно, что функция вещественной переменной x является аналитической, если имеет место сходимость степенного ряда к этой функции в интервале 
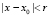, тогда как для функции комплексной переменной это условие значит, что существует ряд Тейлора, сходящийся к этой бесконечно дифференцируемой функции.
Можно утверждать о наличии у аналитических функций конечной производной в точке x0. А также справедливо обратное утверждение: при существовании производной функции конечной в области x0, функция в этой области аналитическая. Пусть дана функция f(z) и точка z0, в окрестности которой данная функция голоморфна. Тогда на основании (1) использование оператора
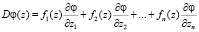
тоже даст функцию голоморфную в окрестности точки z0. К функциям, полученным в результате итеративных операций, также справедливо применение этого свойства.
(2)
А следовательно, функции, полученные при использовании операторов типа (2), могут быть записаны в виде регулярных сходящихся степенных рядов. При формальном объединении множителя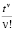 
и голоморфной функции Dvf(z), получится ряд вида
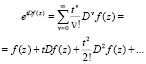, (3)
где t – новая переменная, не зависящая от переменных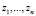 
. Подобные ряды были впервые использованы норвежским математиком Софусом Мариусом Ли. Они имеют ряд характерных свойств, некоторые из которых следуют из правил нахождения производной и дифференциала суммы и произведения [1, с. 186].
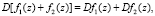(4)
(5)
(6)
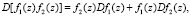(7)
где в соотношениях (5) и (6) параметр с понимается либо как собственная постоянная, или имеет смысл функции, не зависящей от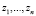 
согласно соотношению (3).
Применив итерацию (2) и дополнив следующим условием
,
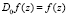обобщим соотношения (4)–(7)
(8)
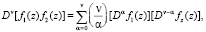
ν = 0, 1, 2, ... (9)
Очевидно, из соотношения (8) вытекает правило суммирования рядов Ли, полученных с использованием единого оператора D:
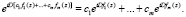
Имеется правило и для нахождения произведения указанных рядов, полученных с использованием единого оператора D:
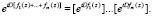
Указанное правило может быть доказано следующим образом. Допустим, m = 2 (количество сомножителей). Используя соотношение (9), получим
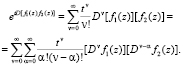(10)
Введем в последнем соотношении (10) в выражении с двойной суммой новый индекс суммирования β = ν – α, после чего можно увидеть как оба индекса α и β, совершенно не завися один от другого, принимают все неотрицательные значения. Заменив в том же выражении последнего соотношения tν на произведение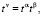 
правую часть можно представить в виде
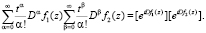
Нетрудно заметить, что возможно обобщение и на большее количество сомножителей.
Используя рассматриваемый класс операторных рядов, можно выполнять инверсию функции распределения, что вытекает из нижеприведенного заключения [2, c. 551].
Пусть дана однозначная аналитическая функция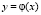 
, тогда функция обратная ей в окрестности точки 
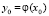и имеющая в указанной окрестности производную 
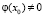, может быть представлена следующим рядом:
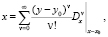(11)
полученным посредством оператора
(12)
На основе вышеуказанного утверждения можно сформулировать метод инверсии функции распределения в общем виде.
Положим, что функция F(x) есть функция распределения, отображающая значение x в вероятность P, а также имеется некоторая точка области существования случайной величины X0, в которой указанная функция принимает какие-либо значения
,
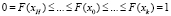где плотность распределения f(x0) ≠ 0. Тогда, на основании вышеуказанного утверждения, покажем, что
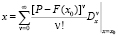(13)
есть обратная функция квантилей [3, c. 480].
Причем обязательным условием существования (13) является то, что функции F(x) аналитическая и производная 
не равна нулю.
Очевидно, что сходимость рядов является необходимым условием использования соотношения (13). Опираясь на условия сходимости функциональных рядов, возможно найти такое число β > 0, при котором ряд (13) сходится абсолютно для
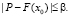
Определим на основании признака Даламбера ограничение β, найдя предел [4, c. 80]:
= 
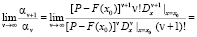
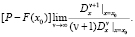
Причем очевидно, что данный оператор преобразования имеет следующее свойство:
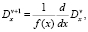
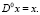
Откуда условие сходимости ряда (13) уже будет иметь вид
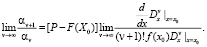
Следовательно,
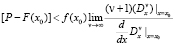
или
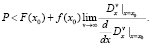
Конечное ограничение (3) имеет вид
Для решения конкретной задачи нужно преобразовать значение β в левой части при заданном законе распределения, взять 
, для которого во всей области существования случайной величины выполняется сходимость ряда (13), а чтобы получить обратные функции распределения одномерной случайной величины, необходимо следующее:
- выбрать точку x0 из такой области, в которой можно разложить функции распределения в ряд (13);
- далее вывести зависимость для оператора (12) в явном виде;
- на основании (11) вывести в явном виде соотношение (13).
Используя характеристические функции и применяя операторные ряды, можно сформировать квантильные функции [5, c. 56].
Видно, если интегрируемая по всей действительной оси характеристическая функция φ(t) функции распределения F(x) имеет вид
,
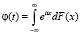то на основании формулы обращения
.
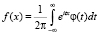Оператор преобразования D в соотношении (13) может быть записан в виде
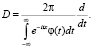(14)
Выберем опорную точку x0 = 0. Очевидно, если x0 = 0, то на основании свойств характеристических функций φ(t) функции распределения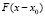 
может иметь вид [6, c. 62]
.
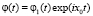Далее, последовательно применим оператор (14). А затем, после вычислений, получим
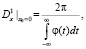
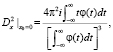
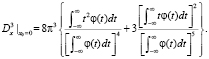
Для использования в конкретных случаях целесообразно результат записать в следующем виде:
,
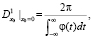
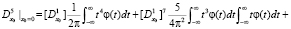
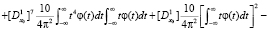
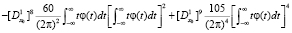и т.д.
Отсюда можно утверждать, что, не применяя формулы обращения, возможно получить для случайной величины X квантильной функции в следующем виде:
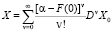, (15)
причем, при условии задания распределения случайной величины φ(t).
Отметим соответствие суммы не имеющих зависимость случайных величин и характеристической функции, равной произведению их характеристических функций. Это следует из мультипликативного свойства х.ф. Отсюда видно вполне эффективное применение (15), без необходимости строить функции распределения сумм случайных величин.
Приведем пример с использованием рассмотренной процедуры построения квантильных функций [7, с. 1083]. Пусть Zn обозначает сумму случайного числа нормальных величин. Тогда х.ф. Zn имеет вид
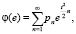
где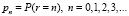 
Можно утверждать, что
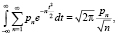
и т.д.
Отсюда сумма случайного числа случайных величин Zn, на основании (15), может иметь вид
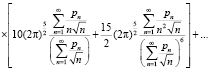
где 