Проблема повышения эффективности функционирования лесопромышленного комплекса не может быть преодолена без решения задач построения оптимального баланса производства и потребления биомассы древесины. Традиционно в задачах такого вида в качестве исходных данных выступают объемы производства лесоматериалов [1, 2], при этом виды лесоматериалов, получаемых на лесосеке, и их объем зафиксированы и неизменны. Решением задачи в такой постановке являются объемы потоков лесоматериалов каждого вида от лесосек к перерабатывающим предприятиям.
На практике лесозаготовительное предприятие в зависимости от сложившейся конъюнктуры на рынке может варьировать виды вырабатываемых с одной и той же лесосеки сортиментов и их количество. Это обусловлено тем, что ствол дерева может быть раскряжеван различными способами с целью получения сортиментов определенного вида, которые могут быть переработаны лесопотребителями.
Например, в регионе имеются предприятия, потребляющие еловый пиловочник длиной 5 м, еловый баланс длиной 4,5 м, еловые строительные бревна длиной 5 м и дрова 5–4 м. Каждый вид лесоматериала характеризуется: породой; максимальным и минимальным диаметром в верхнем отрезе; длиной; качественными характеристиками (допустимыми пороками). В данных условиях, если рассматривать еловый ствол длиной 16 м, имеется, по крайней мере, два варианта раскряжевки: «пиловочник + баланс + дрова»; «строительное бревно + баланс + дрова». Следовательно, возникает более сложная задача оптимизации портфеля заказов, связанная с многовариантностью использования древесины.
Подход к определению портфеля заказов, основанный на принятии многовариантности выхода сортиментов с лесосырьевой базы, позволяет оптимизировать выбор технологических цепочек производства и потребления лесоматериалов по критерию наиболее выгодного использования лесного фонда.
Анализ работ [3, 4] и др. показывает, что решение задачи по формированию оптимального портфеля заказов может осуществляться на основе применения средств экономико-математического моделирования, численных методов решения задач математического программирования, а также информационных технологий.
Задача оптимизации портфеля заказов тесно связана с проблемой оптимального раскроя ствола дерева. Задача оптимального раскроя сводится к определению рациональных вариантов поперечного деления ствола дерева на сортименты, удовлетворяющих определенному условию максимума, в частности наибольшей стоимости вырабатываемых сортиментов, максимальному использованию древесины ствола и др. Среди отечественных исследований, посвященных анализу процесса оптимальной раскряжевки стволов, можно отметить работы B.C. Петровского, Г.А. Степакова, А.С. Ледяева, И.И. Тихонова, Е.В. Воробьевой и др. [5–7]. За рубежом также ведутся исследования в этом направлении [8, 9].
Цель данного исследования заключается в разработке математических моделей, обеспечивающих оптимизацию портфеля заказов для лесозаготовительных предприятий с учетом многовариантности выхода сортиментов с лесосырьевой базы.
Постановка задача оптимизации портфеля заказов нами была изложена в работе [10]. Для ясности излагаемого материала кратко приведем суть постановки задачи. Имеются запасы леса с известными значениями его параметров для каждого лесного участка, где предполагается проводить лесозаготовки. Известны лесоперерабатывающие предприятия, для каждого из которых определены виды и необходимые объемы лесоматериалов. Имеется транспортная сеть, соединяющая лесные участки и лесоперерабатывающие предприятия. Необходимо выбрать потребителей и объемы реализации им лесоматериалов посредством выбора вариантов раскряжевки хлыстов, с учетом установленного критерия оптимизации. Варьируя способы раскряжевки хлыстов, можно получить различные варианты использования древесины, что соответствует различным схемам реализации лесоматериалов лесоперерабатывающим предприятиям.
Материалы и методы исследования
Задача оптимизации портфеля заказов на основе учета многовариантности раскряжевки стволов деревьев является сложной многоэтапной задачей, требующей выделения ряда последовательных подзадач. Предложено выделить следующие этапы:
1) прогноз выхода стволовой древесины;
2) формирование множества вариантов раскряжевки стволов;
3) определение оптимального портфеля заказов с использованием методов математического программирования.
На первом этапе осуществляется прогноз выхода стволовой древесины с участков, отведенных в рубку. Такие данные могут быть получены на основе материально денежной оценки лесосек. Также для этих целей может быть использована разработанная нами имитационная модель выхода стволовой древесины, описанная в работе [11].
Второй этап предполагает решение задачи формирования множества вариантов раскряжевки стволовой древесины на сортименты. Виды сортиментов, рассматриваемые при формировании множества вариантов раскряжёвки, определяются из анализа потребительского спроса на рынке. Выход сортиментов может быть определен либо по сортиментным таблицам, либо по товарным.
Для решения задачи третьего этапа предлагается следующая модель. Введем необходимые обозначения для описания предмета труда. Пусть k – тип ствола; K – общее количество типов стволов (каждый тип описывается тремя значениями: порода; длина; диаметр у комля),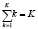 
; Nk – количество вариантов раскряжевки стволов типа k; N – общее количество вариантов раскряжевки стволов, 
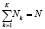; r – вид сортимента; R – общее количество видов сортиментов, 
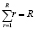; j – вариант раскряжевки; Drkj – количество сортиментов вида r, которые получаются из стволов типа k при варианте раскряжевки j; T – период планирования.
Для описания лесозаготовительных предприятий введем следующие обозначения. Пусть p – лесозаготовительное предприятие; P – общее количество лесозаготовительных предприятий; Mp – множество лесосек, назначенных для рубки лесозаготовительным предприятиям p; M – общее количество лесосек,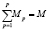 
; i – номер лесосеки; Aik – количество стволов типа k, предназначенных для рубки на лесосеке i; 
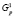– количество стволов, заготовляемых в смену лесозаготовительным предприятием p; Ci – затраты на заготовку одного ствола на лесосеке i.
Для описания перерабатывающих предприятий введем следующие обозначения. Пусть s – деревообрабатывающее предприятие; S – общее количество перерабатывающих предприятий; Brs – количество сортиментов вида r, необходимых перерабатывающему предприятию s;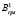 
– количество сортиментов вида r, которое заготовительное предприятие p должно поставить перерабатывающему предприятию s в рамках договоров; 
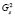– количество сортиментов, потребляемых в смену на перерабатывающем предприятии s; Frs – цена реализации сортиментов вида r перерабатывающему предприятию s.
Введем переменные: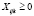 
– количество стволов типа k с лесосеки i, раскряжеванных по варианту j; 
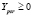– количество сортиментов вида r, поставляемых от лесозаготовительного предприятия p на перерабатывающее предприятие s.
Введем ограничения модели. Количество раскряжеванных стволов типа k не должно превышать числа стволов, имеющихся на лесосеке i:
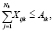для 
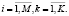(1)
Количество поставляемых сортиментов вида r должно быть больше, чем потребность в них на деревоперерабатывающем предприятии s:
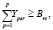для 
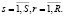(2)
Количество поставляемых сортиментов вида r должно быть больше количества, определенного договорными отношениями между лесозаготовительным предприятием p и перерабатывающим предприятие s:
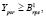для 
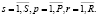(3)
Количество сортиментов вида r, поставляемых лесозаготовительным предприятием p, должно быть меньше или равно количеству сортиментов, поставляемых всем деревообрабатывающим предприятиям:
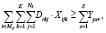для 
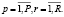(4)
Количество стволов, заготовляемых на лесосеках лесозаготовительного предприятия p за период планирования T, не должно превосходить объема работ, который может быть выполнен за период планирования:
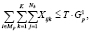для 
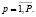(5)
Количество сортиментов, перерабатываемых на перерабатывающем предприятии s за период планирования T, не должно превосходить объема работ, который может быть выполнен за период планирования:
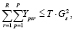для 
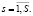(6)
Определение рационального портфеля заказов может осуществляться на основе разных критериев оптимизации. В качестве критериев оптимизации могут выступать: минимизация затрат конкретного лесозаготовительного предприятия или некоторой их совокупности; максимизация прибыли конкретного предприятия или некоторой их совокупности; максимизация прибыли предприятия с минимальной прибылью; минимизация затрат предприятия с максимальными затратами. По нашему мнению, в условиях рыночной экономики целесообразно в качестве критерия оптимизации выбирать прибыль. В таком случае целевая функция модели будет выражать прибыль, получаемую за счет разности между выручкой от продажи лесоматериалов и затратами на их заготовку.
Для конкретного лесозаготовительного предприятия p целевая функция имеет вид
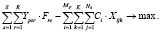(7)
Выражение (7) максимизирует прибыль конкретного лесозаготовительного предприятия.
Целевая функция для определения рационального портфеля заказов для нескольких лесозаготовительных предприятий p:
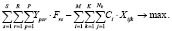(8)
Целевая функция максимизирует прибыль нескольких лесозаготовительных предприятий. Следует отметить, что при использовании целевой функции (8) может сложиться такая ситуация, когда одно или несколько предприятий окажутся банкротами. В таком случае может быть целесообразным введение дополнительного ограничения, при котором количество заготовленных стволов на лесосеках лесозаготовительного предприятия p должно быть больше, чем минимальное количество заготовки:
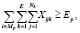для 
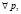(9)
где Ep – минимальное количество стволов, которое должно быть заготовлено на лесозаготовительном предприятии p, чтобы избежать банкротства лесозаготовителя.
Также в качестве критерия оптимальности может быть максимизация прибыли лесозаготовительного предприятия с минимальной прибылью:
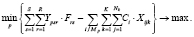(10)
Оптимизация портфеля заказов для конкретного лесозаготовительного предприятия p c учетом транспортных затрат примет вид
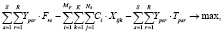(11)
где Tpsr – затраты на транспортировку сортимента вида r от лесозаготовительного предприятия p к обрабатывающему предприятию s.
Для некоторой совокупности предприятий p:
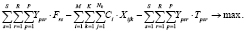(12)
Результаты исследования и их обсуждение
Разработанные модели (1)–(12) позволяют определить оптимальный портфель заказов для лесозаготовительных предприятий с учетом: характеристик предмета труда, вариативность выхода сортиментов; затрат на преобразование предмета труда в готовую продукцию; договорных соглашений между предприятиями отрасли; мощности предприятий по заготовке и переработке биомассы древесины; индивидуальных особенностей предприятий отрасли, исключающих банкротство отдельных лесозаготовительных предприятий. Отличительной особенностью предлагаемых моделей является то, что они позволяют получать рекомендации по способам раскряжевки стволов, а следовательно, рассчитывать оптимальный баланс производства и потребления биомассы древесины с учетом вариативности выхода сортиментов на конкретной лесосеке.
Апробация моделей была проведена при обосновании инвестиционных проектов для предприятий отрасли: ООО «Соломенский лесозавод», ООО «Карлис-Пром», ООО «СтройИнвестРесурс», ООО «Минусинсклес», ООО НПО «Финтек», ООО «Роскомлес».
Следует отметить некоторые сложности в использовании предлагаемых моделей, связанные со временем, затрачиваемым на расчет. Сложность расчетов оптимального портфеля заказов, а следовательно, и их длительность, сильно зависит от количества видов сортиментов, на которые может быть раскряжёван ствол дерева. Опыт применения моделей показал, что задача может быть решена с приемлемой скоростью на настольном компьютере, если рассматривается возможность выпиливания из ствола дерева не более 6–8 видов сортиментов. При увеличении числа сортиментов время расчетов значительно вырастает. В настоящее время нами ведутся исследования по оптимизации расчетов на основе генетических алгоритмов.
Заключение
Традиционно задача построения оптимального баланса производства и потребления биомассы древесины решалась на основе подхода, где в качестве исходных данных предполагаются «зафиксированные» объемы производства сортиментов, получаемых с лесных участков. Однако освоение лесного фонда в своей основе предполагает многовариантность использования древесины, обусловленную тем, что ствол дерева может быть раскряжеван различными способами. Представленные в работе математические модели (1)–(12) позволяют решать задачу построения оптимального баланса производства и потребления биомассы древесины с учетом такой многовариантности. Запасы леса рассматриваются не как константа объема лесоматериалов каждого сортимента, а как гибкая система, подстраиваемая под потребности участников рынка лесной продукции. Сортиментный план лесозаготовительного предприятия динамически формируется в процессе решения задачи выбора лесоперерабатывающих предприятий. Такой подход позволяет рациональнее использовать биомассу древесины и способствует повышению эффективности функционирования лесопромышленного комплекса в целом.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-38-00327 мол_а.