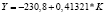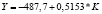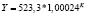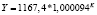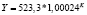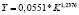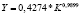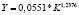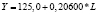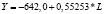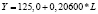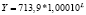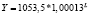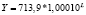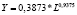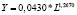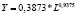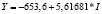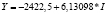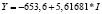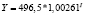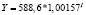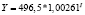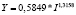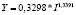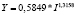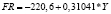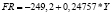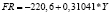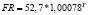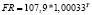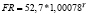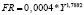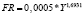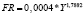Выявление, описание и оценки связей и зависимостей в различных сферах экономики стало важной, первостепенной и актуальной задачей. Решение любой задачи в экономике начинается с подготовки исходного информационного обеспечения. В качестве такового нами выбраны величины нескольких ключевых экономических показателей. Целью настоящего исследования является выявление, описание и анализ взаимосвязей (зависимостей) между парами показателей регионов России и их особенности в разные временные периоды по пространственным данным.
Связи (зависимости) между показателями могут быть одно- и многофакторными. Большинство ученых и специалистов, занимающихся проблемами изучения и оценки взаимосвязей между показателями в экономике, считают, что каждый показатель в экономике связан с множеством других и меняется под их влиянием. Поэтому предпочтение отдают построению, описанию и изучению многофакторных связей (зависимостей).
Однако, с нашей точки зрения, построение, описание и оценка многофакторных связей целесообразно и следует строить и анализировать парные связи, а затем на их основе строить и анализировать многофакторные.
При построении и оценке связей и зависимостей многие ученые ограничиваются построением уравнений регрессии линейного и степенного видов. Связи (зависимости) в экономике носят вероятностный неопределенный характер. Поэтому более правильным является, с нашей точки зрения, построение и анализ и других видов уравнений (показательного, гиперболического, параболического и др. видов). Более того, с нашей точки зрения, для описания одной и той же зависимости могут оказаться приемлемыми два-три вида уравнений регрессии. Именно с таких позиций мы подходили к проведению настоящего исследования.
В табл. 1 приведены величины показателей регионов РФ в разрезе федеральных округов за 2015 г., взаимосвязи между которыми нами исследованы. Из показателей табл. 1 ВРП является результативным (зависимым) показателем, три ресурсных показателя (стоимость основных фондов, численность занятых в экономике, инвестиции) показатели-факторы, от которых зависит ВРП. Сальдированный финансовый результат (СФР) является результативным показателем, который должен зависеть от показателей ресурсов согласно экономической логике. Однако наши исследования показали, что степень корреляционной зависимости СФР от трех показателей-ресурсов оказалось низкой (неудовлетворительной). СФР представляет собой разность между суммой прибыли и суммой убытков. С другой стороны, СФР – часть ВРП, который должен коррелировать с ВРП, т.е. СФР зависит от ВРП. Показатели-факторы (K, L, I) не зависят от ВРП и друг от друга, но они корреляционно связаны. Как известно, в математике, если Y от X, то X в свою очередь зависит от Y. В экономике дело обстоит несколько иначе. Здесь между парой показателей возможны: взаимозависимость; взаимосвязь; первый от второго является зависимым, а второй от первого корреляционно связанным и наоборот.
Для выявления, описания и анализа связей (зависимостей) между показателями требуется построить уравнения регрессии, т.е. рассчитать его параметры. Например, самым простым из уравнений является линейное уравнение Y = b + m + X, где Y, X – зависимый и независимый показатели, которые являются заданными, b и m – параметры, которые требуется рассчитать.
Однако прежде чем построить уравнение регрессии требуется выяснить: во-первых, наличие и степень корреляционной зависимости; во-вторых, возможный его вид, поскольку он заранее однозначно не известен. Чтобы ответить на эти вопросы, требуется рассчитать целую группу статистических характеристик. Сущность, назначение и методику расчета каждой характеристики можно найти в публикациях по эконометрике и компьютерному моделированию [2–5].
С нашей точки зрения, нет необходимости в расчете всех статистических характеристик. В каждом конкретном случае можно ограничиться несколькими, наиболее значимыми из них.
В настоящее время разработаны и широко применяются различные прикладные программы (общего и специального назначения), позволяющие автоматизировать расчеты, связанные с построением уравнений регрессии. В частности, в MS Excel имеется инструментарий встроенных математических, статистических и др. функций, позволяющий рассчитывать параметры статистических характеристик и др. показатели, как в отдельности, так и группами одновременно.
Таблица 1
Величины пяти ключевых экономических показателей регионов России в разрезе федеральных округов за 2015 г.
|
ВРП, млрд руб. |
ОФ, млрд руб. |
Числ., тыс. чел. |
Инвест., млрд руб. |
СФР, млрд руб. |
||
|
Y |
K |
L |
I |
SF |
||
|
1 |
Центральный федер. округ |
20820,6 |
47271 |
19008 |
3673 |
3363,1 |
|
2 |
Северо-Западный фед. округ |
5914,8 |
16021 |
6750,2 |
1439,4 |
933,9 |
|
3 |
Южный федеральный округ |
3920,3 |
9255 |
6161,2 |
1207,5 |
304,2 |
|
4 |
Северо-Кавказский фед. округ |
1587,1 |
3601 |
3464,1 |
508,1 |
26,8 |
|
5 |
Приволжский федер. округ |
9171,1 |
20928 |
14115 |
2447,6 |
1098,2 |
|
6 |
Уральский федеральный округ |
8001,8 |
26777 |
6037,1 |
2514,1 |
1575,4 |
|
7 |
Сибирский федеральный округ |
6106,9 |
13146 |
9010,1 |
1382,8 |
717,4 |
|
8 |
Дальневост. федеральный округ |
3222,5 |
9188 |
3267,5 |
885,7 |
399,5 |
|
Российская Федерация |
58900,7 |
147430 |
67813 |
14556 |
8421,7 |
Для выявления и оценки парных зависимостей требуется создать различные информационные документы (таблицы, графики, диаграммы и др.). Для разработки таких документов нами разработан модельно-компьютерный инструментарий, включающий математическую и компьютерную модели. Под математической моделью понимается совокупность всех формул, которая должна быть создана в ходе решения задачи, куда входят уравнения регрессии, формулы для определения каждой статистической характеристики и каждого параметра уравнения регрессии, формулы для промежуточных расчетов (например, логарифмирование при построении уравнений регрессии степенного вида, формулы суммирования и нахождения средних арифметических значений показателей и др.), формулы для расчета показателей по уравнениям регрессии, такие как предельный эффект и коэффициент эластичности. Перечислить и привести все эти математические формулы, объединенные нами в понятие «математическая модель», нет необходимости.
Компьютерная модель – понятие относительно новое, толкуемое разными авторами по-разному. С нашей точки зрения, компьютерная модель – это совокупность всех компонентов, разрабатываемых на ПЭВМ для создания всех информационных документов, автоматизации расчетов и процедур обработки информации. В рамках компьютерной модели могут быть созданы (при необходимости) дополнительные аналитические информационные документы. При этом целесообразно все созданные информационные материалы (таблицы, графики и др.), необходимые для анализа и иных целей, перенести в текстовый формат (например, в текстовый файл в MSWord) [6].
2005
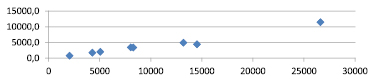
2010
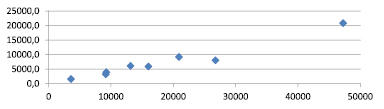
2015
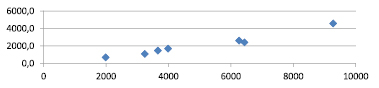
Графики зависимости ВРП от стоимости основных фондов по федеральным округам РФ по данным за 2005, 2010 и 2015 гг.
Выявление связей (зависимостей) между парами экономических показателей целесообразно и следует начинать с построения графиков «точек рассеивания». Отметим, что для многофакторных зависимостей построение графиков невозможно. Однако проверить графически можно наличие корреляции зависимого показателя от каждого из показателей-факторов, включаемых в многофакторное уравнение регрессии.
На рисунке приведены графики, построенные нами для выявления наличия связей (зависимостей) ВРП от стоимости основных фондов по федеральным округам РФ по данным за 2005, 2010 и 2015 гг.
Аналогичные графики построены и для других рассматриваемых парных связей. Анализ этих графиков показывает, что между всеми парами исследуемых показателей имеют место корреляционные связи (зависимости), которые, скорее всего, могут быть описаны уравнениями регрессии линейного, показательного и степенного видов. Проведенные нами расчеты и их анализ подтверждают это предположение.
Анализ уравнений регрессии следует начинать с оценки их приемлемости на основе статистических характеристик. В качестве таковых нами выбраны три характеристики: стандартная ошибка для результативного показателя, индекс детерминации, выражающий степень тесноты связи и критерий Фишера и средняя ошибка аппроксимации [4–6].
В соответствии с проведенным нами сравнительным анализом статистических характеристик рассмотренные нами зависимости являются приемлемыми: наиболее предпочтительной она оказалась для зависимости ВРП от стоимости основных фондов, приемлемой, но в меньшей степени она оказалась для зависимости ВРП от численности занятых в экономике. Напомним, что индекс детерминации принимает значения от 0 до 1, т.е. 0 < r2 < 1. При этом чем ближе численная величина к единице, тем выше степень корреляционной связи (зависимости).
На основе величин статистических характеристик нами сформулированы аналитические выводы, в частности, по величинам индексов детерминации и по величинам средней ошибки аппроксимации. В соответствии с величинами индексов детерминации:
– по трем зависимостям из четырех степень тесноты корреляций связи составляет более 0,92 для уравнений линейного и степенного вида за 2015 г., при этом уравнения линейного вида предпочтительнее степенных уравнений;
– все три вида уравнения, выражающие зависимости ВРП от численности занятых, примерно равно приемлемы по величинам индекса детерминации (составляет 0,63–0,67).
Сравнение величин индексов детерминации для уравнений за 2010 г. с 2005 г. показывает заметное увеличение степени тесноты корреляции для всех трех видов уравнений, выражающих зависимости ВРП от численности занятых в экономике. Из других зависимостей одни повысились, другие снизились. Но все уравнения оказались приемлемыми: величины индекса детерминации являются высокими или очень высокими. Из величин индексов детерминации для 12-ти пар связей в 2015 г. для 6-ти пар теснота корреляционной зависимости оказалась выше, а для других 6-ти – ниже (для всех уравнений Y от L, двух уравнений Y от I и одного уравнения для зависимости FR от Y), чем в 2005 г.
Анализ приемлемости парных связей (зависимостей) по величинам средней ошибки аппроксимации (А, %) показал, что:
– за 2005 г. линейные Y от К, У от I получили оценку «хорошо», FR от Y – «удовлетворительно», Y от L – «неудовлетворительно», три показательных уравнения» (Y от К, Y от L, Y от I) получили оценку «хорошо» и одно уравнение – «удовлетворительно», все четыре уравнения степенного вида по А получили оценку «хорошо»;
– за 2010 г. линейное уравнение получило одну оценку «удовлетворительно», остальные – неудовлетворительно; для трех уравнений показательного вида величины (А) имеют оценку «хорошо», а одно уравнение – «неудовлетворительно»; все четыре уравнения степенного вида имеют оценку «хорошо», за 2015 г. только одно линейное уравнение оказалось приемлемым (А = 19,4 % можно считать удовлетворительным); все показательные и степенные уравнения оказались приемлемыми с оценкой «хорошо».
Таким образом, большинство построенных уравнений парной регрессии, выражающих линейные, показательные и степенные виды зависимостей, оказались приемлемыми для описания и оценки исследуемых связей (зависимостей).
Конечной задачей исследователя–аналитика является определение и оценка ряда показателей, ради которых в конечном итоге строятся уравнений регрессии [3, 4, 6]. Для уравнений парной регрессии к таким показателям относятся: предельные эффекты и эластичности затратно-ресурсных показателей. Они рассчитываются по формулам 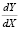 и
и 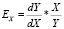 соответственно. Сущность и экономический смысл этих показателей можно найти в публикациях [3, 4].
соответственно. Сущность и экономический смысл этих показателей можно найти в публикациях [3, 4].
Таблица 2
Виды и математическая запись уравнений парной регрессии, выражающие зависимости между ключевыми показателями федеральных округов за разные временные периоды
|
2005 |
2010 |
2015 |
|
|
Y от K |
|||
|
лин |
Y = –487,7 + 0,5153*K |
|
|
|
показ |
|
|
|
|
степ |
|
|
|
|
Y от L |
|||
|
лин |
|
|
|
|
показ |
|
|
|
|
степ |
|
|
|
|
Y от I |
|||
|
лин |
|
|
|
|
показ |
|
|
|
|
степ |
|
|
|
|
FRот Y |
|||
|
лин |
|
|
|
|
показ |
|
|
|
|
степ |
|
|
|
Примечание. Y – ВРП, млрд руб.; K – стоимость основных фондов, млрд руб.; L – численность занятых в экономике, тыс. чел.; I – инвестиции, млрд руб.; FR – сальдированный финансовый результат, млрд руб.
Виды построенных нами уравнений парной регрессии и их математическая запись приведены в табл. 2.
Предельные эффекты показывают рост зависимого показателя в денежных измерителях на единицу роста показателя фактора, а коэффициент эластичности – рост результативного показателя в процентах на однопроцентный рост показателя-фактора.
Заслуживают внимания два особых случая: в случае линейной зависимости предельный эффект показателя-фактора равен параметру при этом факторе, т.е. 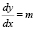 ; в случае зависимости степенного вида коэффициент эластичности показателя-фактора равен показателю степени, т.е. Ex = m. Величины предельного эффекта и коэффициента эластичности для построенных нами уравнений парной регрессии приведены в табл. 3.
; в случае зависимости степенного вида коэффициент эластичности показателя-фактора равен показателю степени, т.е. Ex = m. Величины предельного эффекта и коэффициента эластичности для построенных нами уравнений парной регрессии приведены в табл. 3.
По величинам предельного эффекта для линейных уравнений из табл. 1 можно отметить следующее:
а) для уравнения Y от К величины предельного эффекта можно выразить неравенством за 2005 г. больше, чем за 2015 г., а последнее, в свою очередь, больше чем за 2010 г. (2005 г. > 2015 г. > 2010 г.);
б) для уравнений Y от L получены следующие соотношения: 2005 г. > 2015 г. > 2010 г., для Y от I: 2010 > 2005 > 2015, для FR от Y: 2005 г. > 2010 г. > 2015 г.
Таблица 3
Величины предельного эффекта и коэффициента эластичности (параметров m) для уравнений парной регрессии линейного и степенного видов
|
Годы |
Y от К |
Y от L |
Y от I |
FR от Y |
|
Для линейного вида |
||||
|
2005 |
0,5153 |
0,2060 |
5,6168 |
0,3104 |
|
2010 |
0,4132 |
0,5525 |
6,1310 |
0,2476 |
|
2015 |
0,4235 |
1,0055 |
5,4280 |
0,1641 |
|
Для степенного вида |
||||
|
2005 |
1,2376 |
0,9375 |
1,3158 |
1,7882 |
|
2010 |
0,9899 |
1,2670 |
1,3391 |
1,6931 |
|
2015 |
0,9544 |
1,2189 |
1,2102 |
0,7893 |
Примечание. Y – ВРП; K – стоимость основных фондов; L – численность занятых в экономике; I – инвестиции; FR – сальдированный финансовый результат.
Такие же соотношения можно определить по величинам коэффициента эластичности для уравнения степенного вида:
а) для уравнения Y от К коэффициент эластичности за 2005 г. больше, чем за 2010, а за 2010 г. больше, чем за 2015 г.;
б) для Y от L: 2010 г. > 2015 г. > 2005 г.;
в) для Y от I: 2010 г. > 2005 г. > 2015 г.;
г) для FR от Y: 2010 г. > 2005 г. > 2015 г.
Как видно из данных табл. 2, за 2010 и 2015 гг. предельный эффект и коэффициент эластичности резко выросли для уравнений, выражающих зависимость ВРП от численности занятых в экономике, для уравнений, выражающих остальные зависимости – предельные эффекты и коэффициенты эластичности уменьшились. Это свидетельствует об ухудшении эффективности использования ресурсов.
Сформулируем некоторые выводы из данных табл. 2:
а) по величинам предельного эффекта для уравнений регрессии линейного вида:
– для зависимости Y от К предельный эффект оказался максимальным по данным 2005 г., по данным за 2010 г. этот показатель существенно снизился, следующие пять лет эффект практически остался на уровне 2010 г.;
– предельный эффект для зависимости ВРП от численности занятых в экономике (Y от К) имеет четко выраженную тенденцию роста (эффект каждые пять лет удваивался), что является фактом положительным, свидетельствующим о росте отдачи от использования рабочей силы;
– предельный эффект для зависимости Y от I имеет свои особенности: в 2010 г. он заметно вырос, но в 2010 г. он снизился и оказался ниже уровня 2005 г., что является фактом отрицательным;
– четкая, но отрицательная тенденция наблюдается по предельным эффектам для зависимости сальдированного финансового результата от ВРП (FR от Y);
– в 2010 г. он снизился на 20 %, а в 2015 г. еще на 35 %;
б) по величинам коэффициентов эластичности для уравнений степенного вида (уменьшение коэффициентов эластичности свидетельствует о снижении эффективности использования ресурсов):
– для зависимости Y от К по пятилетиям имеет место тенденция уменьшения (с 1,24 % в 2005, до 0,99 в 2010 и до 0,95 в 2015 г.);
– величина коэффициента эластичности для зависимости Y от К в 2010 г. существенно выросла (более чем на 30 %), в 2015 г. уменьшилась по сравнению с 2010 г., но была заметно больше, чем в 2005 г.;
– эластичность инвестиции в 2005 и 2010 гг. практически была на одном уровне, но в 2015 г. она уменьшилась на 10 % по сравнению с 2005 г.;
– эластичность ВРП по отношению к сальдированному финансовому результату в 2010 г. снизилась на 5 %, но в 2015 г. снижение составило 2,3 раза (с 1,79 до 0,79 %).
Таким образом, анализ показывает, что за три временных периода 2005, 2010 и 2015 гг. из трех ключевых ресурсов экономики регионов России (стоимости основных фондов, численности занятых в экономике, инвестиции) повышение эффективности использования наблюдается только для одного ресурса – численности работников; эффективность использованных двух денежных ресурсов – ухудшилась.