Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Большой практический и академический интерес к методам принятия управленческих решений активно способствовал становлению и развитию теории и практики кластерного анализа на графах [1]. Широкий и постоянно растущий спектр прикладных задач сформировал устойчивый запрос на алгоритмы для взвешенных, ориентированных, знаковых и нечетких графов, а также графов причинно-следственных связей, отличительными характеристиками которых являются большая размерность и наличие циклов. В данной работе предпринята попытка методом бенчмаркинга – эталонного сопоставления на известных наборах данных [2] – выявить алгоритмы, эффективные с учетом современной динамики теоретико-графовых моделей данных

Для понятия «кластер», «когезионная подгруппа» или «сообщество» существует ряд различных и иногда противоречивых определений. Объединяет их понятие группы тесно связанных между собой узлов, которая, в свою очередь, слабо связана с остальной частью сети. Любая функция качества для назначения узлов в сообщества следует простому принципу: объединить все, что связано, и не разделять то, что связано не явно.

Для решения этой задачи ряд алгоритмов требует указания на входе параметров, таких как количество кластеров и разного рода пороговых значений. Другие алгоритмы не используют входных параметров либо вычисляют их самостоятельно.

Ряд существующих методов позволяет формировать пересекающиеся кластеры, которые допускают вхождение одной вершины сразу в несколько сообществ. Отдельные алгоритмы работают с понятием «шума» – точками, которые не принадлежат ни одному из кластеров. Многие алгоритмы кластеризации допускают существование аутлаеров – кластеров с единственной вершиной.

Растущий интерес к парадигме больших данных подчеркивает значение вычислительной сложности и времени работы алгоритмов.

В нашем эксперименте мы постарались охватить все типы алгоритмов, перечисленные выше.

Материалы и методы исследования

Для эксперимента были взяты 18 графовых наборов данных с различным соотношением числа вершин и дуг, а также различным распределением весов на дугах.

Для части графов известно истинное разбиение на кластеры, для другой части – нет. Графы с известным разбиением на кластеры были выделены в отдельную группу. Оставшиеся графы были разбиты на две равные группы: в одну попали графы, средняя степень которых не превышает двух, в другую – графы с более плотными связями между вершинами. Характеристики графов представлены в таблице.

После формирования эталонных графовых наборов данных были определены алгоритмы кластеризации для эксперимента.

Часть алгоритмов, а именно SCAN, Spectral, LPA и Walktrap, реализована в библиотеке Lightcluster. Алгоритмы Infomap и Spinglass реализованы в библиотеке Igraph. Обе библиотеки написаны для языка программирования Python.

Все алгоритмы, за исключением алгоритма LPA, используют в своей работе различные входные параметры.

Алгоритм Infomap использует механизм случайного блуждания [3]. Проблема изоляции сообществ в графе понимается как задача кодирования пути, через который пройдет путник, с минимизацией длины присвоенного кода. У каждого сообщества есть свой собственный уникальный двоичный код. В сообществе у каждой вершины есть свой собственный уникальный внутренний код, у вершин из различных сообществ может быть тот же самый код. Кроме того, есть дополнительный код завершения, который не соответствует главным кодам в этом сообществе. Кодирование пути происходит следующим образом: когда вершина попадает в другое сообщество, его код и внутренний код вершины фиксируются. Когда вершина переходит к другому сообществу, пишется код завершения для этого сообщества и код для нового, то есть кодирование происходит на сообществах и вершинах.

В основе алгоритма LPA или LabelPropagation лежит следующий принцип [4]: узел принадлежит сообществу, которому принадлежит большинство соседей. В начале расчета каждый кластер состоит из одной вершины. Далее метки кластеров пересчитываются итеративно. На каждом шаге вершины случайным образом перетасовываются, и вершины обновляют свои идентификаторы согласно меткам соседних вершин. Процесс завершается, когда каждая вершина оказывается с той же самой меткой, что и наибольшее число ее соседей. Можно видеть, что при использовании параметров по умолчанию первоначальное распределение вершин происходит случайным образом, что может приводить к разным результатам при нескольких расчетах.

Для алгоритма SCAN требуется задать количество смежных с вершиной вершин (µ), а также радиус соседства (μ). На основе этих двух параметров вычисляется плотность кластера [5]. Данный алгоритм позволяет выделить пересекающиеся кластеры, а также шум.

Алгоритм Spectral основан на нахождении собственных значений матриц, связанных с графом, и собственных векторов лапласиана графа [6]. Далее применяются известные алгоритмы кластеризации, например, k-средних.

Алгоритм Walktrap также использует метод случайного блуждания на графах. Идея состоит в том, что при случайном блуждании по графу вероятность остаться в одном кластере значительно выше, чем выйти за пределы этого кластера, поскольку между кластерами проходит меньше ребер, чем их насчитывается в кластере [7].

Описание графовых наборов данных для бенчмаркинга

Алгоритм Spinglass используется понятие спинового стекла из физики, когда при намагничивании частицы получают отрицательный или положительный заряд или спин. Как известно, при нагревании ферромагнитные сплавы теряют свое свойство, и заряды частиц в сплаве уравновешивают общее состояние магнитного поля. При понижении температуры ферромагнетик вновь обретает свое свойство, при этом частицы группируются позарядно, положительно заряженные – с положительно заряженными, а отрицательно заряженные – с отрицательными. Данный метод работает с ориентированными графами и учитывает веса дуг [8].

Для оценки эффективности и сравнения алгоритмов между собой нами использовались следующие метрики качества.

Для оценки кластеризации графов с известным разбиением можно использовать F-меру Ван Ризенбергена (F1 score, F score), которая нашла широкое применение в теории информационного поиска [9]. Эта характеристика, которая позволяет дать оценку одновременно по точности (precision) и полноте (recall). В контексте задачи кластеризации точность – это число вершин, попавших в кластер, соответствующий истинному кластеру, деленное на общее число вершин в истинном кластере, в то время как полнота – это число вершин, попавших в кластер, соответствующий истинному кластеру, деленное на общее число вершин в кластере. F-мера может быть интерпретирована как взвешенное среднее этих двух метрик, которое изменяется в диапазоне от единицы до нуля, где 1 – это наилучший результат.

Сложнее оценить качество кластеризации в случае, когда истинное разбиение неизвестно.

Модулярность – относительно новая, но популярная метрика была предложена М. Гирваном и М. Ньюманом [10]. Значение метрики лежит на интервале между 0,5 и 1, рассчитывается по формуле

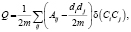
где A – матрица смежности, Aij (i, j) – элемент матрицы, di – степень i-й вершины, Сi – кластер, в котором находится вершина, m – количество дуг в графе. δ(Сi, Cj) = 1, если Сi = Cj, в противном случае 0.

Преимущество модулярности состоит в том, что достаточно легко рассчитать прирост модулярности в случае перемещения некоторого количества вершин между кластерами, не пересчитывая заново метрику.

Удалив все ребра между полученными кластерами, мы получим два незавизимых подграфа или так называемый разрез графа [2]:

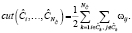
Нормализовав группы вершин на объем занимаемый ими в графе, мы получим нормализованный разрез графа (Normalized Cut):

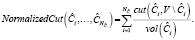
Идея относительного разреза (Ratio Cut) графа состоит в том, чтобы заменить значение 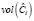каждого блока его размером – количеством вершин графа 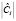. В этом случае мы можем описать относительный разрез следующей формулой:

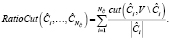
Заметим, что указанные метрики в базовой постановке неприменимы для оценки качества пересекающихся кластеров, требуется их модификация.

Результаты исследования и их обсуждение

При анализе результатов на основе модулярности (рис. 1) можно выделить графы, хорошо поддающиеся кластеризации, и графы с плохой или неудовлетворительной кластеризацией. Графы Uni reresearch, Crime, «Качество системы нематериальной мотивации», «Качество корпоративной культуры», «Качество корпоративного управления» и Performance продемонстрировали плохую тенденцию разбиения на подграфы, что может говорить о некоторой структурной особенности этих графов, затрудняющей их кластеризацию. Все вышеперечисленные графы находятся во второй подгруппе, то есть в той группе графов, средняя степень которых выше двух. В то же время графы dolphins, «Политика президента Южной Кореи», Deployment, Sustainable Banking и football поддаются более качественному разбиению.

Из всех алгоритмов, представленных в статье, наилучшие результаты показали алгоритмы Spinglass и Walktrap. При этом метод Spinglass демонстрирует лучший показатель по метрике Modularity относительно метода Walktrap.

Метод Spectral в целом показал хорошие результаты, за исключением графа Sustainable Banking. Кроме того, следует отметить нестабильность этого метода относительно других алгоритмов. Большую нестабильность можно наблюдать только у алгоритма SCAN, единственного из алгоритмов, который работает с пересекающимися кластерами.

В силу особенностей метрик Ratio Cut и Normalized Cut верхняя граница метрик не определена, что затрудняет визуальное восприятие графиков при оценке качества разбиения на кластеры.

На графах, для которых было известно истинное разбиение (рис. 2), алгоритм Spinglass не потерял своих позиций, достаточно точно распределив вершины по кластерам и даже добившись идеального разбиения в графе Zachary Karate Club, что можно объяснить небольшим количеством идеальных кластеров на выходе.

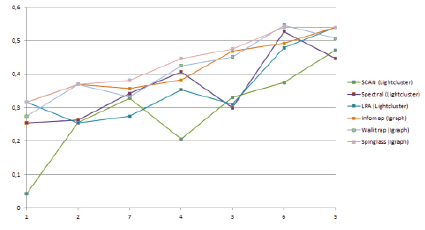
Рис. 1. Значения метрики модулярности для графов со степенью больше 2

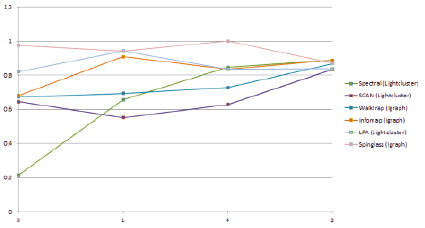
Рис. 2. Значения метрики F-мера для графов с известным разбиением на кластеры

В то же время метод Walktrap не попал в первую тройку. Это можно объяснить двумя причинами. Во-первых, мы не задавали в данном случае алгоритму явных значений входных параметров, позволив ему вести расчет с параметрами, которые он вычислял самостоятельно. Вторая причина может заключаться в том, что данный алгоритм вычисляет результат, подбирая оптимальное значение метрики модулярности, в то время как в графах, моделирующих реальную практическую ситуацию, значение метрики модулярности может отличаться от идеального.

Метод Spectral для графов с известным разбиением показал худший результат, особенно на модели Sustainable Banking.

Особенно нужно выделить алгоритм SCAN, еще одного аутсайдера. Эталонные графы были выбраны нами с расчетом того, что не имеют вершин, принадлежащих одновременно нескольким кластерам. Метод SCAN, ориентированный на выявление пересекающихся кластеров, выделил много именно таких пересекающихся кластеров.

Заключение

В этой статье мы рассмотрели основные типы алгоритмов кластеризации графов. Оценка эффективности и сравнение алгоритмов проводились на основе таких метрик качества, как F-мера, модулярность, нормализованный и относительный разрезы графа. В ходе эксперимента шестью алгоритмами была произведена обработка 18 эталонных графов, разделенных на подгруппы на основе средней степени графа, отражающей сложность отношений между вершинами.

На основе результатов эксперимента может быть сделано заключение о том, что среди представленных алгоритмов кластеризации нет универсального алгоритма, который бы значительно опередил остальные на всех наборах данных. Лидерами бенчмаркинга являются алгоритмы Spinglass и Walktrap. Алгоритм SCAN несколько выбивается из общего ряда алгоритмов и стоит особняком в данном эксперименте. Можно также выделить алгоритм Spectral, получивший высокие оценки на большинстве графов.

При анализе значений метрик качества мы отметили, что при одинаковом разбиении на кластеры получались разные оценки качества кластеризации.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-01-00243.