Построение моделей технологических объектов является весьма важной задачей, так как позволяет предсказать особенности функционирования агрегатов, что способствует достижению требуемых характеристик. Моделирование подразумевает построение такого описания объекта, которое с заданной точностью будет совпадать с функционированием реального объекта.
При решении практических задач, требующих составления и последующего анализа модели, важным критерием является трудоёмкость моделирования. Вследствие этого возникает задача формализации процесса моделирования технологических процессов. На базе формализованного подхода к построению и исследованию моделей является целесообразным создание программного комплекса, автоматизирующего и упорядочивающего научно-исследовательскую и конструкторскую деятельность специалистов, занимающихся разработкой технологического оборудования и систем управления этим оборудованием.
Решение задачи моделирования технологических процессов – это типовой этап научно-исследовательских и опытно-конструкторских работ, проводимых в технической сфере. В том случае, когда моделирование является составной частью работ над проектированием или модернизацией технологического оборудования, к нему могут быть применены стандартные методологии управления проектами, такие как PMBOK, PRINCE2, IPMA и другие [1].
Однако эти методологии не учитывают особенностей проведения научных исследований, а уделяют основное внимание общему течению бизнес-процесса. В связи с этим разработка организационных подходов к проведению научных исследований и, в частности, к моделированию технологических процессов является весьма актуальной задачей.
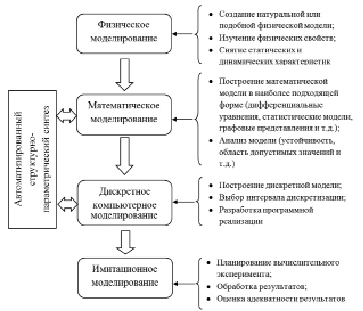
Рис. 1. Схема поэтапного моделирования
Для лучшего представления сущности процесса моделирования следует выделить типовые этапы, а также задачи и механизмы, используемые на них.
Большинство исследовательских работ, связанных с построением и использованием моделей технологических процессов, поддаются разделению на схожие этапы. Типовая последовательность работ подразумевает линейное прохождение следующих фаз: физическое моделирование, математическое моделирование, дискретное компьютерное моделирование, имитационное моделирование (рис. 1).
На этапе физического моделирования производится исследование интересующего технологического процесса. Для этого может быть проведён ряд экспериментов с существующим оборудованием. При отсутствии такой возможности создаются физические модели, отражающие основные закономерности изучаемых процессов.
Основной целью построения физической модели является получение статических и динамических характеристик моделируемого процесса. Таким образом, реализованная и изученная физическая модель даёт возможность формально описать свойства изучаемого процесса, определить численные значения актуальных параметров, оценить их корреляцию и динамику изменения.
После сбора и обработки данных о функционировании физической модели наступает этап математического моделирования. В зависимости от особенностей технологического процесса и целей моделирования могут быть выбраны различные математические аппараты.
В случае прикладных разработок немаловажным фактором является трудоёмкость. Часто бывает целесообразным использовать заведомо менее точную методологию моделирования, однако являющуюся более простой в использовании (например, инженерный метод Зиглера и Никольса выбора параметров ПИД-регулятора [2]).
В случае моделирования схожих процессов целесообразно использование шаблонных подходов, дающих прирост скорости синтеза модели. В этом случае возникает задача хранения базы шаблонов и выбора необходимого шаблона модели по заданным критериям. Благодаря применению систем управления базами данных и базами знаний возможно создание автоматизированной системы, предлагающей на этапе математического моделирования наиболее подходящую методологию и шаблон, используя которые создаётся математическое описание исследуемого процесса.
В некоторых случаях построение математической модели может быть затруднено в связи со сложностью описания исследуемого объекта. В этом случае может быть применён подход «черного ящика», когда модель синтезируется лишь на основании накопленной статистической информации о поведении объекта. Для автоматизации этого процесса предлагается использование эволюционного алгоритма как средства направленного поиска структуры и параметров модели, адекватно описывающей полученные ранее исходные эмпирические данные.
В связи с тем, что создание средства интеллектуального синтеза, которое могло бы работать с разными математическими аппаратами, представляется затруднительным, то для упрощения предлагается использование только математического аппарата сетей Петри.
Автоматизированный структурно-параметрический синтез позволит не только создавать новые модели по исходным данным, но и уточнять (адаптировать) уже имеющиеся или упрощённые модели с целью повышения их адекватности и точности. В этом случае можно говорить о подходе «серого ящика», когда в качестве исходных данных для интеллектуального синтеза модели помимо эмпирических сведений о входных и выходных сигналах используется обобщённая или упрощённая модель исследуемого объекта.
Дискретное компьютерное моделирование стало практически, обязательным этапом процесса синтеза и анализа моделей технологических процессов. Это связано с тем, что численное моделирование по сравнению с аналитическим анализом моделей позволяет проводить исследование модели значительно быстрее, а в некоторых случаях и точнее. Кроме того, корректировка параметров и модификация структуры модели при численной компьютерной реализации происходит значительно оперативнее. В настоящее время существует ряд специализированных прикладных программных пакетов, успешно применяемых при моделировании технологических процессов. Среди них следует выделить такие программные продукты, как Matlab (подпрограммы Simulink [3], FuzzyLogicи д.р.), Mathcad [4], Pipe2 и др.
Реализация дискретной численной модели должна проводиться с учётом особенностей перехода от математической модели к программному алгоритму. В первую очередь это связано с процессом дискретизации, который может привести не только к появлению погрешностей, но и к функциональным различиям с исходной математической моделью (например, потеря устойчивости [5]). Проверку корректности перехода от математической модели к дискретному компьютерному представлению технологического процесса можно представить в качестве типовых методик, содержащих в себе ряд формальных операций сопоставления численных и функциональных характеристик модели до и после дискретизации. Процесс применения этих методик также подлежит автоматизации благодаря использованию программных средств поддержки научных исследований.
Этап имитационного моделирования связан с исследованием свойств реализованной на предыдущем этапе дискретной компьютерной модели. Применение статистических и аналитических инструментов обработки результатов численных экспериментов, а также их планирования позволяет получить не только отдельные численные результаты функционирования модели технологического процесса для единичных выборок исходных условий, но и выявить качественные особенности поведения моделируемых систем и объектов, обладающих схожими характеристиками.
Имитационное моделирование, как правило, включает в себя итеративный процесс запуска дискретной компьютерной модели с различными наборами исходных данных. Полученные результаты подлежат дальнейшей обработке для выявления функциональных зависимостей и обобщения результатов.
В качестве примера использования поэтапного моделирования приводится процесс изучения работы трубной шаровой мельницы с целью создания системы автоматического управления [6].
Этот технологический агрегат представляет собой сложную систему, которая состоит из вращающегося корпуса с внутрикорпусными элементами, мелющих тел и непосредственно частиц измельчаемого материала.
На первом этапе проводилось физическое моделирование, которое заключалось в наблюдении за процессом помола в промышленных и лабораторных установках. Анализ численных и функциональных характеристик процесса помола, полученных для технологических установок в различных режимах работы, позволил выявить основные процессы, протекающие в данном технологическом агрегате, и выделить основные характеристики агрегата, оказывающие наибольшее влияние на технологический процесс.
Для проведения математического моделирования выбранного объекта следует выбрать соответствующий математический аппарат. Так как целью исследования является синтез модели системы автоматического управления технологическим агрегатом, то в качестве основного инструментального средства выбирается сеть Петри. Согласно предлагаемому подходу на данном этапе производится поиск наиболее уже решённых научно-технических задач, из которых могут быть заимствованы актуальные в контексте решаемой задачи модели, функциональные зависимости и статистические данные. Исходя из исследования трубной шаровой мельницы как объекта управления будет применена передаточная функция по каналу управления (подача материала – загрузка мельницы) в виде апериодического звена с запаздыванием:
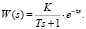 (*)
(*)
Так как моделирование предполагает работу с аналоговой информацией, то для описания системы автоматического управления будет использована модификация сети Петри – информационная сеть Петри (ИСП).
Для упрощения процесса составления модели производится поэтапное моделирование отдельных элементов системы. Упрощённую динамическую модель (рис. 2), соответствующую передаточной функции (*), можно составить из трёх отдельных блоков, реализующих простейшие функции:
1. Блок, реализующий динамику апериодической функции;
2. Блок, реализующий функцию запаздывания распространения сигнала;
3. Блок, реализующий функцию масштабирования.
Приведённая модель имеет два входа: In1– вход модели, на который подаётся информация о подаче материала, In2 – вход масштабирующего блока, позволяющего настраивать диапазон изменения выходного сигнала. Выход модели Out1 передаёт информацию о текущей загрузке шаровой мельницы. В соответствии с принципами работы ИСП выходной сигнал нормирован в диапазоне [0; 1].
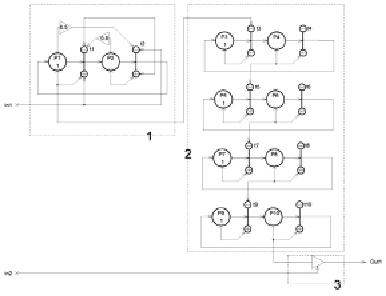
Рис. 2. Динамическая модель трубной шаровой мельницы
Для уточнения модели применяется автоматизированный структурно-параметрический синтез, основная идея которого заключается в применении генетического алгоритма для адаптации исходной модели к заданным условиям [7]. В качестве исходных данных для адаптации выступают эмпирические данные, накопленные на первом этапе (физическое моделирование), и упрощённая модель, созданная на втором этапе (математическое моделирование).
Процесс адаптации может быть разделён на две чередующиеся фазы: структурный синтез и параметрический синтез. Во время фазы параметрического синтеза происходит подбор параметров модели (в данном случае происходит поиск коэффициентов усиления информационных дуг). Во время структурного синтеза модификации подлежит сетевая структура, то есть происходит изменение множеств позиций, переходов и дуг их соединяющих.
Так как в качестве инструмента автоматизированного синтеза применяется генетический алгоритм, то для уточнения исходной модели достаточно задания целевой функции, направленной на минимизацию разницы между собранными эмпирическими данными и результатами численного моделирования.
Для лучшей сходимости генетического алгоритма применяется интеллектуальная настройка параметров его работы при помощи нейронной сети, обученной на типовых ситуациях, возникающих при работе эволюционного алгоритма.
Благодаря использованию математического аппарата сетей Петри переход к третьему этапу (дискретное компьютерное моделирование) значительно упрощается. Это связано с тем, что модель, представленная в виде сетевой структуры, может быть автоматически преобразована в численную модель, предназначенную для обработки на вычислительной системе. Таким образом, адаптированная математическая модель шаровой мельницы автоматически транслируется в исполняемый алгоритм, пригодный для дальнейшего исследования.
На четвёртом этапе проводится имитационное моделирование, целью которого является выявление функциональных зависимостей между производительностью шаровой мельницы и её геометрическими размерами.
Результат этих экспериментов представляет собой набор результатов при различных исходных значениях. Используя регрессионный анализ, подбирается функциональная зависимость, удобная для дальнейшего применения в инженерных расчётах.
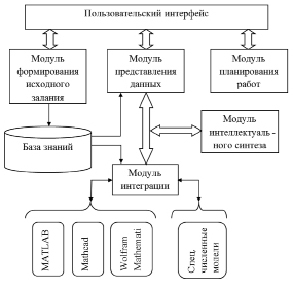
Рис. 3. Структура программного средства автоматизации процесса моделирования
Приведённая последовательность этапов моделирования может быть упорядочена и формализована с применением программных средств автоматизации научных исследований.
Для реализации подхода поэтапного моделирования был разработан программный продукт (рис. 3), позволяющий автоматизировать и процесс моделирования благодаря использованию средств управления исследовательской деятельностью.
Рассмотренный программный комплекс, реализующий подход поэтапного моделирования, позволяет контролировать и оценивать процесс моделирования не только по окончанию работ, но и на промежуточных стадиях. Это даёт возможность оперативного управления ходом исследовательских работ.
Применение эволюционного алгоритма для синтеза модели исследуемого объекта позволяет сократить время, затрачиваемое на разработку новой математической модели, а также упрощает адаптацию уже имеющихся математических описаний в соответствии с актуальными условиями.
Таким образом, предложенный подход поэтапного моделирования технологических процессов, включающий использование интеллектуального структурно-параметрического синтеза, позволяет упорядочить процесс научных исследований. В том случае, когда результаты этих исследований являются исходными данными для проведения конструкторских работ, это особенно важно, так как позволяет ускорить общий ход выполнения научно-исследовательских и опытно-конструкторских работ.



