Трудно назвать отрасли мировой промышленности, где бы не использовались дифференциальные, планетарные, замкнутые дифференциальные зубчатые передачи. Их применение не только повсеместно, но и осуществляется в таких масштабах, что не может быть даже приблизительно оценено в объемах. Ими оснащаются транспортные, грузоподъемные, металлообрабатывающие, металлургические, полиграфические, текстильные и сельскохозяйственные машины, военная техника, морской флот. Любое их совершенствование, увеличение их коэффициента полезного действия является актуальной задачей, имеющей государственное значение.
В настоящей статье обосновывается и решается принципиальная, по мнению авторов, проблема планетарных передач, которая вот уже на протяжении более чем векового их применения не была чётко сформулирована, а потому и не находила разрешения. Речь идёт о возможности существенного увеличения КПД, а также уменьшения массы и габаритов планетарных передач самого различного назначения.
Коротко эта проблема сводится к следующему – все ныне эксплуатируемые и заново создающиеся планетарные передачи при расчёте их массо-габаритных параметров, прочности и передаваемой мощности рассматриваются как передачи, оснащённые одним сателлитом, через который передаётся вся мощность от ведущего колеса к ведомому водилу или наоборот. Это утверждение не голословно.
Один из ведущих учёных – специалистов в области изучения и проектирования планетарных передач – профессор В.Н. Кудрявцев в монографии [2], основываясь на многолетнем опыте создания и эксплуатации планетарных передач, доказательно утверждает, что при работе многосателлитных планетарных передач реально до 80 % мощности передаётся через один сателлит, а потому, чтобы обеспечить необходимую прочность этих высоконагруженных передач, следует их силовой расчёт проводить из условия, что вся мощность от ведущего звена к ведомому передаётся через один сателлит. Важно отметить, что в любой момент времени эта нагрузка может передаваться через разные сателлиты, а потому каждый из сателлитов должен обладать прочностью, удовлетворяющей полному его нагружению. При этом считается, что участие других сателлитов в передаче мощности может лишь дополнить прочность редукторов в целом и их долговечность.
Естественным становится вопрос о том, как следует изменить конструкции многосателлитных планетарных передач, чтобы гарантировать равное участие всех сателлитов в передаче мощности. Если бы этого удалось добиться, то нагрузки, действующие на каждый сателлит, могли бы быть уменьшены в (число сателлитов) раз, а это неизбежно привело бы к уменьшению массо-габаритных параметров передач (в разы), что дало бы легко прогнозируемый высокий экономический эффект, имеющий революционный результат.
Исходя из отмеченного, можно утверждать, что проблема многосателлитных планетарных зубчатых передач как минимум должна быть дополнительно глубоко изучена с высокой ожидаемой практической целесообразностью.
Изучению планетарных передач были посвящены сотни, а может быть, и десятки сотен монографий, обзоров, научных статей. Эта тема широко освещается в учебниках и учебных пособиях по теории зубчатых передач. Достаточно назвать монографии Н.Ф. Руденко [1] в 47 печатных листов, В.Н. Кудрявцева [2], Л.Н. Решетова [3], М.А. Крейниса и М.С. Розовского [4], Н.А. Чусовитина [5] и др. Казалось бы, теория таких передач к настоящему времени вполне разработана и каких-либо принципиальных сомнений не вызывает. И тем не менее, по глубокому убеждению авторов настоящей статьи, существует оставшаяся практически не разрешенной и, можно предположить, даже не очень замеченной на протяжении полутора веков – от первых исследований Р. Виллиса до настоящего времени проблема, которая может быть сформулирована как проблема многосателлитности планетарных передач.
Известно, что подвижность любого плоского механизма, а планетарная передача с цилиндрическими зубчатыми колесами есть плоский механизм, может быть определена по широко известной формуле подвижности, называемой расширенной формулой П.Л. Чебышёва, имеющей вид
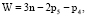 (1)
(1)
где n – число подвижных звеньев, р5 и р4 – числа кинематических пар соответственно пятого (шарниры) и четвертого (высшие пары – пары сцепления зубьев колес) классов.
На эту формулу ссылаются в своих монографиях Н.Ф. Руденко, В.Н. Кудрявцев, Л.Н. Решетов и другие, считая ее вполне приемлемой для решения задач определения подвижности планетарных передач.
Если применимость формулы (1) к исследованиям подвижности планетарных передач не вызывает сомнений, то ее использование в частных случаях безусловно правомочно, и если такие сомнения у исследователей возникали, то, во-первых, авторам настоящей статьи эти сомнения неизвестны, а во-вторых, вопрос о ее несоответствии особенностям планетарных передач должен был быть чётко сформулирован и безупречно доказан, что также в известной литературе не найдено.
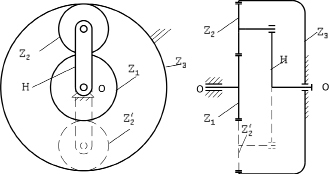
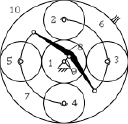
Рис. 1. Простейшая планетарная AI передача
Обратимся к частным примерам. На рис. 1 показана простейшая AI передача (по терминологии Н.Ф. Руденко), где А – означает внешнее (Ausen), а I – внутреннее (Innen) зацепление колес.
В этой передаче согласно общим обозначениям, приведенным И.И. Артоболевским в учебнике [3], всего три подвижных звена: Z1 – центральное подвижное колесо, Z2 – сателлит, Н – водило. Центральное колесо Z3 (венец) неподвижно. Число кинематических пар р5 = 3 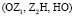 , а пар р4 = 2 – это зацепления
, а пар р4 = 2 – это зацепления 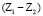 и
и 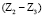 . По формуле (1) имеем W = 9 – 6 – 2 = 1, т.е. механизм вполне работоспособен, в нем при заданном движении центральному колесу Z1 или водилу Н все остальные звенья могут двигаться вполне определенно.
. По формуле (1) имеем W = 9 – 6 – 2 = 1, т.е. механизм вполне работоспособен, в нем при заданном движении центральному колесу Z1 или водилу Н все остальные звенья могут двигаться вполне определенно.
Если обратиться к учению Ассура, то этот механизм состоит из ведущего звена Z1 и группы звеньев Z2 – Н, обладающей нулевой подвижностью, т.е. являющейся группой Ассура. В этой группе два звена – Z2 и Н, две пары р5 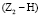 и
и 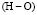 и две пары р4
и две пары р4 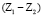 и
и 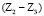 . Подвижность этой группы W = 0. Если же за ведущее звено принять водило Н, то рассматриваемый механизм будет состоять из ведущего звена (Н) и группы нулевой подвижности – колес Z2 и Z1 с двумя шарнирами р5
. Подвижность этой группы W = 0. Если же за ведущее звено принять водило Н, то рассматриваемый механизм будет состоять из ведущего звена (Н) и группы нулевой подвижности – колес Z2 и Z1 с двумя шарнирами р5 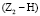 и
и 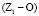 и двумя парами р4
и двумя парами р4 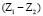 и
и 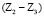 , также обладающей нулевой подвижностью.
, также обладающей нулевой подвижностью.
Эти тривиальные пояснения приводятся здесь, чтобы показать далее, как влияет на подвижность передачи введение второго, третьего и т.д. сателлитов. Так, покажем, что если установить на водило второй сателлит (Z'2 (он показан на рис. 1 штрихами), то общее число звеньев станет равным четырем (n = 4) и, кроме того, в передачу добавятся шарнир р5 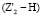 , тогда всего становится р5 = 4 и добавляется р4 = 2 (зацепления второго сателлита со звеньями Z1 и Z3), т.е. станет р4 = 2. Тогда по формуле (1) будем иметь
, тогда всего становится р5 = 4 и добавляется р4 = 2 (зацепления второго сателлита со звеньями Z1 и Z3), т.е. станет р4 = 2. Тогда по формуле (1) будем иметь
W = 12 – 8 – 4 = 0,
т.е. механизм окажется неработоспособным. Эта система по приведенному расчету является неподвижной. Дополнительный сателлит теперь оказывается препятствием для движения в передаче, т.е. определить реакции в кинематических парах такого механизма становится невозможным, а значит, спроектировать его по всем канонам обеспечения прочности нельзя. Выход из создавшейся неопределенности находится достаточно просто – расчеты прочности производятся исходя из условия, что вся мощность передаётся через один сателлит. Если число дополнительных сателлитов, установленных на водило, более одного обозначить как nдс, то есть n дополнительных сателлитов, то общее число звеньев станет (n + nдс), общее число пар р5 будет (р5 + nдс), общее число пар зацепления окажется (р4 + 2 nдс), так как каждый дополнительный сателлит будет входить в зацепление с центральным колесом и с неподвижным венцом. Подвижность передачи тогда с дополнительными сателлитами Wдс определится как
Wдс = 3(n + nдс) – 2(р5 + nдс) – (р4 + 2nдс) = 3n – 2р5 – р4 – nдс
или
Wдс = W – nдс,
где по (1) W = 1 и тогда
Wдс = 1 – nдс. (2)
При введении в механизм, например, пяти сателлитов, что в планетарном редукторостроении считается вполне допустимым, подвижность всей передачи становится равной –4, и система оказывается четырежды статически неопределимой. Этот результат и является основанием к утверждению, что сформулированная в названии статьи проблема многосателлитных планетарных передач существует и она до настоящего времени не разрешена.
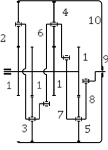
Приведенные выше аргументы достаточно обоснованы, опровергнуть их невозможно, но любой опытный инженер или исследователь, исходя из практики эксплуатации планетарных передач с тремя и более сателлитами, может вполне справедливо заявить, что такие передачи серийно и массово изготавливаются и повсеместно применяются в самых различных отраслях техники, что проблем с их подвижностью просто не существует. Именно такие суждения, основанные на опыте, нередко оказываются вредными, не дающими возможности развития идеи на более высоком уровне, не всегда «практика является критерием истины». В рассматриваемом конкретном случае просто отбросить как не имеющий практического значения результат (2), получаемый из формулы (1), не является оправданным. Важнее ответить на вопрос, почему получаемый результат, а именно отрицательная подвижность механической системы – многосателлитной планетарной передачи – не проявляется на практике? А исчерпывающий ответ на этот вопрос существует. Дело в том, что высшие кинематические пары, которые используются в зубчатых зацеплениях, т.е. геометрические связи зубьев колес, есть связи неудерживающие, в них в отличие от обычных шарнирных соединений возможна передача движения лишь в одном направлении. Зуб одного колеса, воздействующий на зуб другого колеса, может «отодвигать» собой зуб другого колеса, но не может, изменив направление движения, увлечь его за собой, то есть связь между зубьями разорвется. Из этого следует, что при некоторых возможных зазорах между зубьями, они, зубья, могут и не соприкасаться друг с другом. Следовательно, когда, например, трехсателлитная передача оказывается вполне подвижной, то это означает лишь, что в зацеплении участвует всего один сателлит, а у второго и третьего сателлитов имеются зазоры с центральными колесами, которые возникли при изготовлении колес, а также в период сборки и доводки передачи. В этом легко убедиться, измеряя зазоры между зубьями в любой работоспособной многосателлитной передаче. Как только эти зазоры исчезнут, окажутся нулевыми, принудить передачу к движению будет невозможно в полном соответствии с формулой (1). Из этого следует вывод, который наиболее четко изложил В.Н. Кудрявцев в работе [2]. Он на рис. 2 показывает реальное расположение зубьев в планетарной передаче и записывает буквально следующее, – «В реальной передаче с фиксированными осями центральных колес и водила, вследствие неизменности погрешностей, касание будет только с одним сателлитом».
Именно из этого соображения делается важный вывод о том, что, рассчитывая на прочность зубья планетарных передач, необходимо исходить из условия, что вся передаваемая мощность в них передается через один зуб, при этом между остальными парами зубьев существуют зазоры. Из изложенного следует, что в действительности в планетарных передачах число пар р4 (зацеплений) не три, а одна, и поэтому в строгом соответствии с формулой (1) обеспечивается определенность движения. Стремление же к более точному изготовлению соединений зубьев с целью полного устранения зазоров, во-первых, практически невозможно, а во-вторых, вредно, так как в этом случае передача оказывается с подвижностью W < 1 т.е. неподвижной. Следует отметить еще и то, что упругие деформации пары зубьев, находящихся в зацеплении, могут приводить лишь к увеличению зазоров между невошедшими в зацепление зубьями, а не уменьшать их, как может показаться.
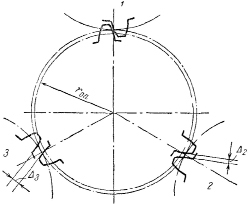
Рис. 2. Зацепление зубьев колес планетарной передачи по В.Н. Кудрявцеву
Всё изложенное выше дает основание сделать следующий вывод – в многосателлитных планетарных передачах, способных передавать мощность одинаково всеми сателлитами, непосредственная установка на выходное звено – водило более одного сателлита недопустима, такие механизмы или в принципе неработоспособны, или могут передавать мощность лишь через один сателлит. Исторически сложилось так, что теоретическое обоснование идеи применения зубчатых передач с колесами, геометрические оси которых подвижны (сателлитами), произошло в сороковых годах восемнадцатого века в исследованиях английского учёного Р. Виллиса. Именно он доказал работоспособность таких механизмов и их принципиальное достоинство. Формула определения передаточных отношений планетарных и дифференциальных зубчатых передач до настоящего времени носит имя Виллиса. Вывод его формулы основывается на условии использования одного сателлита на водиле. Очевидной тогда оказалась и идея параллельной – одинаковой установки на водило других сателлитов, что априори предполагалось допустимым. Проверить это было невозможно, так как какой-либо формулы для определения подвижности механизмов еще не существовало.
Если встать на позицию полного доверия к истинности результатов, которые дают формулы подвижности механических систем, обоснованные П.Л. Чебышёвым [7], А.П. Малышевым [19], В.В. Добровольским [13], И.И. Артоболевским [20], то безответственного заявления вроде «мало ли, какой результат дают эти формулы, машины же работают» будет недостаточно. Надо тогда доказать, что есть ситуации в технике, где формула подвижности или неверна, или может быть проигнорирована. Но таких доказательств не существует, а потому единственным верным подходом к созданию совершенных машин является подход фундаментально базирующийся на полном удовлетворении формул подвижности. Основываясь на этом положении применительно к многосателлитным планетарным передачам, следует внимательно изучить приведённую выше формулу (1). Сущность ее заключается в том, что первый ее член 3n определяет полный состав движений системы из n звеньев в плоскости ее функционирования. Одно звено имеет три независимых подвижности – две вдоль осей X и Y плоской системы координат и одно движение – вращательное относительно оси, перпендикулярной плоскости XY. Каждая кинематическая пара – шарнир р5 оставляет одно относительное движение в плоскости, а два других исключает, тогда р5 таких шарниров исключают 2р5 подвижностей. Каждая высшая пара (зацепления) – двухподвижная, дозволяет единственное движение, а именно в направлении нормали в точке касания, а это значит что р4 таких пар накладывает р4 условий связи.
Разница между 3n и (2р5 + р4) определяет подвижность рассматриваемой кинематической цепи. В случае, когда на водило планетарной передачи устанавливаются одинаковым образом как первый сателлит через шарнир р5, так и дополнительные сателлиты числом nдс, кинематическая цепь получит отрицательную подвижность
3n – (2р5 + р4) < 1,
то есть подвижность цепи оказывается отрицательной, если
(2р5 + р4) > 3n.
Эту ситуацию можно исправить лишь введением дополнительных звеньев – рычагов nдс. Но их установка в цепь потребует использования дополнительных шарниров р5 в количестве, удовлетворяющем баланс
(3n –1) = (2р5 + р4). (3)
Иного способа исправления неработоспособности многосателлитных планетарных передач не существует. Так, если создаётся планетарная передача с (1 + nдс) сателлитами, то общее число подвижных звеньев в ней станет
n = (1 + nдс) + 2 + nдр, (4)
где 2 – это входное – центральное зубчатое колесо и выходное звено – водило, а nдр – число дополнительных рычагов. При этом число звеньев (1 + nдс) сателлитов образует (1 + nдс) шарниров, входное колесо и водило добавляют в цепь два шарнира в их соединениях с неподвижным колесом – стойкой и потребуется еще nдр шарниров для присоединения к цепи дополнительных рычагов, т.е. таких кинематических пар – шарниров потребуется
р5 = (1 + nдс) + 2 + nдр. (5)
Кроме того, каждый из сателлитов, входящий в зацепление с центральными колесами, добавляет в цепь по две высших кинематических пары, т.е. всего
р4 = 2(1 + nдс). (6)
При условиях (4), (5) и (6) зависимость (3) преобразуется к виду
3[(1 + nдс) + 2 + nдр] – 1 = + 2[(1 + nдс) + 2 + nдр] + 2(1 + nдс),
откуда
nдр = nдс. (7)
Таким образом, чтобы обеспечить определенность движения всех звеньев планетарной зубчатой передачи при увеличении числа сателлитов в ней, необходимо в ее кинематическую цепь вводить дополнительные рычаги числом, равным числу дополнительных сателлитов.
Если в цепи используется один сателлит, то в ней nдс = 0, nдр = 0 и из (4), (5) и (6) следует n = 3, р5 = 3, р4 = 2. Этому условию удовлетворяет передача, приведенная на рис. 1. Если же в цепь вводится дополнительно один сателлит nдс = 1, то необходимо в нее, согласно (7), ввести дополнительный рычаг nдр = 1. Тогда общее число звеньев по (4) станет равным n = 5, число шарниров по (5) р5 = 5 и число пар по (6) р4 = 4.
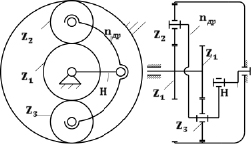
а) б)
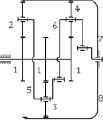
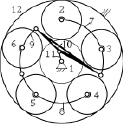
Рис. 3. Двухсателлитная одноподвижная планетарная передача
Кинематическая цепь такой планетарной двухсателлитной передачи показана на рис. 3.
В ней обозначены Z1 – центральное входное колесо, Z2 – сателлит, Z3 – дополнительный сателлит, Н – водило, nдр – дополнительный трехпарный рычаг, который тремя шарнирами соединен с сателлитами Z2, Z3 и с водилом Н.
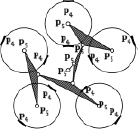
В профильной плоскости передачи (рис. 3, б) центральное входное колесо показано дважды в зацеплениях с сателлитами Z2 и Z3, что обеспечивает полную ясность введения nдр – дополнительного рычага. С точки зрения структурной теории Ассура этот механизм состоит из входного звена Z1 и присоединённой к нему группы Ассура, т.е. группы, обладающей нулевой подвижностью и не распадающейся на более простые группы. Эта группа показана на рис. 4. В её состав входят два сателлита Z1 и Z2, дополнительный рычаг nдр и водило Н. В этой группе четыре звена Z1, Z2, nдр и Н, четыре пары р5 – шарниры и четыре высшие пары, р4 – зацепления сателлитов с центральным подвижным и неподвижными колесами.
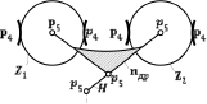
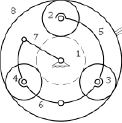
Рис. 4. Не распадающаяся на простые четырехзвенная группа нулевой подвижности двухсателлитной планетарной передачи
Числа звеньев и кинематических пар сложных многосателлитных планетарных передач с увеличением чисел сателлитов от 0 до 10 показаны в табл. 1.
Таблица 1
Общее число звеньев n, общее число шарниров р5, общее число высших пар р4, а также число дополнительных рычагов nдр в зависимости от числа вводимых дополнительных сателлитов nдс
|
nдс |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
n |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
22 |
|
р5 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
22 |
|
р4 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
|
nдр |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
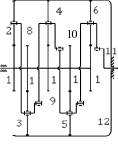
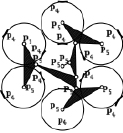
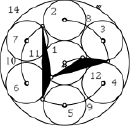
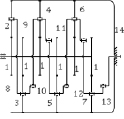
В строгом соответствии с табл. 1 в табл. 2 показаны реальные конструкции самоустанавливающихся трех, четырех, пяти и шестисателлитных планетарных передач, обладающие подвижностью W = 1.
Все эти планетарные передачи, во-первых, самоустанавливающиеся, а во-вторых, содержат в своем составе не распадающиеся на простые группы звеньев нулевой подвижности.
Заключение
Предложенные в настоящем исследовании метод поиска и реальные конструкции уравновешенных многосателлитных передач позволяют создавать планетарные передачи, в которых все установленные в них сателлиты нагружаются одинаково и расчет прочности всей передачи в них сводится к расчету прочности одного сателлита, нагрузка на который при этом уменьшается в (число сателлитов) раз.
Таблица 2
Трех, четырех, пяти и шестисателлитные планетарные передачи с подвижностью W = 1
|
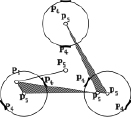
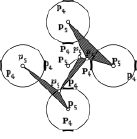
Нераспадающаяся группа Ассура, используемая в передаче |
Самоустанавливающаяся планетарная передача |
|
|
Вид в фас |
Вид в профиль |
|
|
n = 6, p5 = 6, p4 = 6
|
Патент № RU (11) 2 541 049 (13) |
|
|
n = 8, p5 = 8, p4 = 8
|
Патент № Ru (11) 2 583 320 (13) |
|
|
n = 10, p5 = 10, p4 = 10
|
Патент № Ru(11) 2 622 731 (13) |
|
|
n = 12, p5 = 12, p4 = 12
|
Заявка на патент отправлена |
|