На широкополосных станах холодной прокатки (ШСХП) при перевалках комплекты рабочих валков с подушками перемещают по стальным плитам 1 (см. рисунок). Для снижения коэффициента трения снизу к подушкам прикрепляют сменные направляющие планки скольжения 2, изготовленные из антифрикционной бронзы БрА9ЖЗЛ [1]. В процессе эксплуатации по мере изнашивания бронзовых планок нарушается точность позиционирования байонетного узла в муфтах, соединяющих рабочие валки с головками карданных валов. При достижении износом планок предельного значения возникает критическое смещение рабочих валков относительно головок карданных валов, при котором их соединение невозможно. Это приводит к отказу главной линии и вынужденному простою стана для замены направляющих планок.
Как показывает практика, ресурс изнашиваемых планок крайне мал: момент отказа наступает через два-три месяца, что приводит к существенному уменьшению технических, технологических и экономических показателей предприятия. Поэтому продление срока службы главного привода по критерию работоспособности направляющих планок скольжения является весьма важной и актуальной проблемой производства холоднокатаного листа.
При решении такого рода задач в настоящее время используют полученные на основе обработки многочисленных экспериментальных данных статистические модели параметрических отказов исследуемых трибосопряжений [2–4]. Однако их практическое применение для оценки текущего износа и ожидаемого ресурса исследуемых узлов трения требует либо предварительного проведения модельных или натурных испытаний опытных образцов, либо специальных экспериментальных исследований для получения тех или иных входящих в модели физических величин, что связано с существенными материальными и временными затратами.
Существенное снижение или полное устранение затрат возможно при использовании чисто теоретических моделей отказов трибосистем с использованием современных представлений о физической природе процессов фрикционного взаимодействия, повреждаемости и разрушения элементов узлов трения из известных материалов в заданных условиях эксплуатации. В частности, при построении моделей параметрической надежности исследуемых трибосопряжений в работах [5–7] предложено описывать процесс изнашивания поверхностей трения как кинетический, развивающийся во времени процесс постепенной повреждаемости и разрушения материалов поверхностных слоев и накопления дефектов их структуры на различных масштабных уровнях, а для его математического моделирования энерго-механическую концепцию изнашивания.
Для решения подобной задачи, рассматриваемой в данной работе, – поиска эффективных способов снижения скорости изнашивания направляющих планок скольжения подушек рабочих валков и продления ресурса главного привода – ниже представлена аналитическая модель их параметрических отказов по критерию износостойкости материалов поверхностных слоев.
Модель построена на основополагающих принципах теории проектной оценки надежности деталей машин [5] с использованием базовых зависимостей энерго-механической концепции изнашивания стационарных узлов трения [6, 7], которые выведены путем совместного решения системы уравнений молекулярно-механической и структурно-энергетической [8–10] теорий трения.
Разработка модели износовых отказов планок скольжения подушек рабочих валков
Разрушение контактной поверхности бронзовых направляющих планок 2 происходит при их перемещении по стальным закаленным плитам 1 с постоянной скоростью скольжения Vск (см. рисунок). Сила Fn прижатия каждой направляющей планки скольжения 2 к плите 1 равна одной четвертой веса комплекта валков с подушками. В процессе эксплуатации к произвольному моменту времени t каждая планка изнашивается на величину yt.
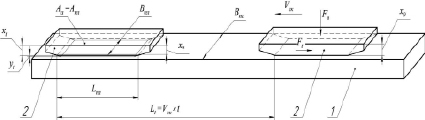
Расчетная схема взаимодействия бронзовых планок 2 со стальными плитами 1
Согласно общей теории проектной оценки надежности стационарных узлов трения [5, 6] для оценки текущего состояния планок скольжения используем изменяющийся во времени основной геометрический размер – их толщину xt (см. рисунок). В процессе деградации каждой планки со средней скоростью изнашивания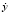 
параметр xt снижается от начального значения xt = x0 до предельного – xt = x*, которое устанавливается в нормативных документах [1]. В качестве допущения принимаем, что сопряжение работает в стационарном режиме трения и усталостного изнашивания в нормальных условиях эксплуатации и смазки без схватывания и заедания поверхностей. Кроме того, будем пренебрегать незначительным увеличением площади контакта при изнашивании планок из-за трапецеидальной формы их боковых поверхностей (см. рисунок) и снижением в связи с этим контактных давлений.
В этих условиях изменение технического состояния каждой планки 2 (см. рисунок) в процессе эксплуатации можно представить уравнением [5, 6]:
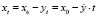. (1)
Решением относительно t = t* уравнения
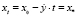, (2)
которое характеризует предельное состояние планки, определим выражение для оценки их проектного ресурса:
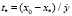. (3)
Для оценки скорости изнашивания планок скольжения используем основную зависимость (кинетическое уравнение) энерго-механической теории изнашивания стационарных трибосопряжений [6, 7]:
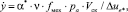(4)
где α* – коэффициент перекрытия площади трения планки;
v – коэффициент превращения работы сил трения в изменение внутренней энергии поверхностного слоя планки;
fмех – механическая составляющая коэффициента трения;
Vск, ра – скорость скольжения элементов сопряжения и контактное давление;
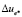– критическая плотность скрытой энергии структуры материала планки.
Система уравнений (3)–(4) и описанных ниже математических выражений для определения входящих в них параметров представляет постановку однопараметрической краевой задачи физической теории надежности стационарных узлов трения «плита 1 – планка 2». Для получения однозначного решения сформулированной задачи и разработки модели отказов исследуемой пары трения необходимо задать условия однозначности, которые включают отличительные признаки сопряжения, начальные и граничные условия [6, 7].
Ниже для проектной оценки ресурса исследуемых пар трения «плита 1 – планка 2» представлен алгоритм решения системы (3)–(4), в котором отличительные признаки рассматриваемой трибосистемы, начальные и граничные условия краевой задачи сформулированы в соответствующих блоках.
Блок 1. Исходные данные.
Представленные в этом блоке параметры и зависимости вместе с расчетной схемой (см. рисунок) определяют отличительные особенности исследуемого объекта и начальные условия краевой задачи.
1 группа. Геометрические параметры. Lпл и Bпл – длина и ширина планки; x0, x* – начальное и предельное значение толщины планки, см. рисунок.
2 группа. Силовые и кинематические параметры. Fn и Ft – нормальная и касательная силы в сопряжении; Vск – относительная скорость скольжения трибоэлементов, см. рисунок.
3 группа. Микрогеометрические параметры. Ra1, Ra2 – среднеарифметическое отклонение профиля трущихся поверхностей; Δ1 – комплексный параметр шероховатости поверхности плиты.
4 группа. Физико-механические параметры поверхностных слоев плиты 1 и планки 2 (см. рисунок), μ1,2 и E1,2 – коэффициенты Пуассона и модули упругости материалов; σпц1,2, σT1,2 и σB1,2, – пределы пропорциональности, пределы текучести и пределы прочности материалов; НB1,2 и НV1,2 – твердость по Бринеллю и Виккерсу поверхностей плиты 1 и планки 2 соответственно; αэф1,2 и ρ1,2 – коэффициенты гистерезисных потерь и плотность материалов поверхностных слоев.
5 группа. Теплофизические параметры. ΔHS1,2 – энтальпия плавления материалов плиты 1 и планки 2 соответственно; α1,2 и λ1,2 – коэффициенты теплоотдачи и коэффициенты теплопроводности материалов трибоэлементов; ue02 – плотность потенциальной составляющей внутренней энергии материала планки в исходном состоянии [6]:
.
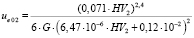6 группа. Фрикционные характеристики. τ0, β – параметры сдвиговой прочности молекулярной связи трущихся поверхностей [8].
Блок 2. Расчет геометрии контакта и свойств материалов поверхностных слоев [11–13], (см. рисунок).
2.1. Площадь контакта –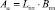 
; площади трения – 
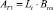и 
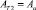; коэффициенты перекрытия – 
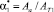и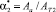 
.
2.2. Периметры площади трения: плиты –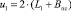 
; планки – 
.
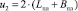2.3. Нормальное напряжение (давление) на контакте: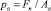 
.
2.4. Механические характеристики материалов: пределы пропорциональности – σпц 1,2 = (0,9÷0,97)•σТ1,2; модули сдвига –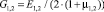 
; упругие постоянные – 
.
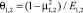Блок 3. Оценка параметров преобразования внешней энергии (граничные условия) [6].
3.1. Коэффициент изменения внутренней энергии материалом поверхностного слоя плиты –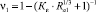 
, где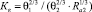 
.
3.2. Коэффициент изменения внутренней энергии материалом поверхностного слоя планки: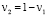 
.
Блок 4. Расчет полного коэффициента трения по зависимостям [8, 11], определяющим граничные условия задачи.
4.1. Напряжение в контактном слое планки:
.
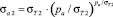4.2. Условия для оценки напряженного состояния контактного слоя планки [6]:
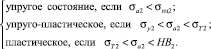
4.3. Полный коэффициент трения в функции вида напряженного состояния материала контактного слоя в период приработки:
– упругое состояние:
;
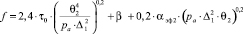– упруго-пластическое состояние:
;
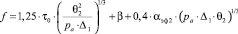– пластическое состояние:
.
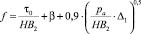Блок 5. Оценка коэффициента трения в установившемся режиме работы [8, 12, 13].
5.1. Стационарные температуры поверхности плиты и планки соответственно
,
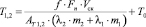где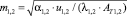 
.
5.2. Упругие постоянные материалов:
.
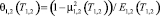5.3. Коэффициент трения:
.
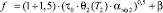5.4. Механическая составляющая коэффициента трения:
.
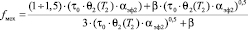Блок 6. Расчет критической плотности энергии изнашиваемого материала [6].
6.1. Приращение плотности тепловой составляющей внутренней энергии:
.
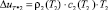6.2. Энергоемкость структуры материала контактного слоя планки (критическая плотность скрытой энергии):
.
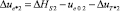Блок 7. Оценка долговечности исследуемого сопряжения.
7.1. Стационарная скорость изнашивания поверхности планки (см. уравнение (4)):
.
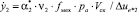7.2. Проектный ресурс трибосопряжения (см. уравнение (3))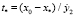 
.
Очевидно, что предложенный алгоритм позволяет рассчитывать ожидаемый ресурс t* направляющих планок подушек рабочих валков для заданных условий будущей эксплуатации без проведения дополнительных лабораторных или промышленных экспериментов. С его помощью возможно аналитически решать задачи конструирования наиболее износостойких планок скольжения и, следовательно, прогнозировать эффективное повышение долговечности главного привода.
Заключение
Сформулирована модель постепенных отказов привода прокатных валков широкополосных станов холодной прокатки по критерию износостойкости направляющих планок скольжения подушек рабочих валков. Она реализована в виде блочного алгоритма, который позволяет:
– рассчитывать текущий износ направляющих планок для условий будущей эксплуатации;
– выполнять теоретические исследования влияния конструктивных и технологических параметров на износостойкость исследуемых сопряжений, аналитически исследовать и выбирать наиболее эффективные варианты, обеспечивая требуемый уровень долговечности главного привода.