Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В работе [1] рассмотрена проблема компьютерного распознавания задач, поступающих на вход классификатора из предметной области учебной дисциплины «Численные методы». Описание каждого объекта ω (задачи) задается совокупностью признаков, т.е. характерных особенностей присущих каждой задаче [1, 2]. Для каждого объекта ω строится информационный вектор признаков I(ω) = {I1(ω), I2(ω),….Im(ω)}, где m – количество признаков. С помощью исчисления предикатов вектор I(ω) преобразуется в вектор с булевыми переменными 0 или 1 [3, 4]. В результате чего получается совокупность векторов 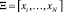, где xi – вектор признаков, принадлежащих i-тому классу, 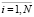. Через N обозначено количество классов предметной области. Порядок следования элементов определяется путем ранжирования по убыванию значения байесовской вероятности, что позволяет сократить перебор классов при обучении системы. В работе рассматривается задача обучения системы процедуре безошибочной классификации объектов по классам с помощью персептрона.

Цель работы

Построение математической модели и программного обеспечения для эффективного распознавания образов с помощью алгоритма обучения Хебба.

Распознавание образов с помощью алгоритма обучения

В самом общем понимании задача распознавания образов состоит в том, чтобы как можно более точно, а в идеале однозначно, установить факт принадлежности исследуемого объекта одному из известных классов или доказать отсутствие возможности сделать это [5, 6]. Сложностью и одновременно особенностью задачи распознавания является то обстоятельство, что признаки, характеризующие классифицируемый объект, могут быть элементами описания многих классов. Это означает, что решающие правила классификатора должны ставить в соответствие каждому классу вполне определенный набор признаков, или признаки имманентные этому и только этому классу. Естественно, что при изменении состава класса, например, в случае выделения в нем нескольких подклассов, число классификационных признаков будет возрастать.

Высказанные соображения позволяют утверждать, что, даже если вероятность принадлежности признаков исследуемого объекта к некоторому классу значительно больше, нежели к другим, это не может служить основанием для однозначного отнесения его к данному классу. Тем не менее вероятностный подход остается весьма продуктивным, поскольку на базе байесовских оценок дает возможность сформировать начальный весовой вектор 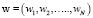для вычисления решающей функции, в качестве которой выступает скалярное произведение .

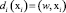Пример реализации этой идеи для классификации задач учебной дисциплины «Численные методы» был рассмотрен в работе [1].

Весовой вектор w = (w1, w2, w7, w4, w3, w5, w6) = (0,25, 0,215, 0,17, 0,143, 0,1, 0,0712, 0,0358), а решающие функции получим следующим образом:

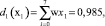
аналогично

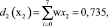
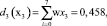
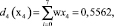
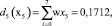
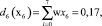
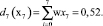
Полученный результат не означает, что система окончательно классифицировала объект. Для однозначной классификации, которую мы в дальнейшем будем именовать правильной, необходимо получить решающую функцию, такую, что di(хi) > 0, если x∈Ω_i и d_j(х) ≤ 0 для всех j ≠ i. Это достигается с помощью методов обучения персептрона, в ходе которого меняются компоненты весовых векторов, поступающих на вход персептрона. Последовательность изменений, алгоритм реализации которых будет описан ниже, продолжается до тех пор, пока не будет достигнуто условие правильной классификации. В силу процедуры построения, решающая функция d(x) представляет собой скалярное произведение, а равенство (w, x) = 0 определяет положение разделяющей гиперплоскости в пространстве Rn, которая является границей открытого множества, содержащего условие правильной классификации.

Принципиально схема работы персептрона представлена на рис 1. Сигнал х = (x1, x2,…., xn) поступает на реагирующий элемент, который вычисляет значение решающей функции и выбирает некоторое действие в зависимости от получаемого результата.

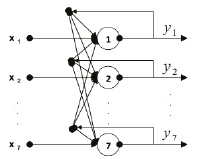
Рис. 1. Архитектура полносвязной нейронной сети

Говоря более конкретно, вектор х = (x1, x1,…., xn) скалярно умножается на весовой вектор w = (w1, w2,.., wn), если для i-го нейрона величина скалярного произведения (w, xi) стремится к определенному значению yi, то весовой вектор не меняется, в противном случае вычисляется величина ошибки и элементы весового вектора пересчитываются. Коррекция весовых векторов может быть произведена различными методами, такими как итерационный метод, метод Хебба, метод обратного распространения ошибки и т.п. Результат скалярного произведения (w, xk) = t преобразуется в сигнал φ(t) с помощью функции активации, в качестве которой могут быть использованы такие функции, как функция Хэвисайда, функция знака (сигнум), тождественная функция, гиперболический тангенс и т.д. [3].

Таким образом, проблема обучения персептрона практически сводится к задаче построения решающей функции di(x) = (wi, x), которая бы за конечное число шагов разделяла элементы обучающей выборки, в соответствии с условием правильной классификации x∈Ω_i, если di(х) > 0 и dj(х) ≤ 0, для всех j ≠ i.

Для реализации построения такой линейной решающей функции с помощью итерационного алгоритма предварительно обучающую выборку запишем в виде бесконечной циклической последовательности 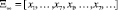[3].

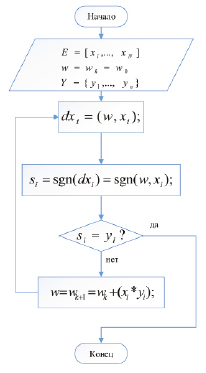
Рис. 2. Блок-схема алгоритма обучения

Идея алгоритма обучения заключается в том, что весовой вектор не меняется, если «предъявленный» вектор классифицируется правильно и увеличивается или уменьшается на величину xk при неправильной классификации (рис. 2) [4].

Представленная на рис. 2 последовательность процедур алгоритма обучения осуществляется в следующем порядке:

1. Формируется циклическая последовательность векторов обучающей выборки. Порядок их определяется по убыванию вероятностей, посчитанных с помощью формулы Байеса, например, (см. таблицу), Ξ_∞ = [x1, x2, x3_7, x4, x5_3, x6_5, x7_6, x1, x2, x3_7, x4, x5_3, x6_5, x7_6,…] = (0,25; 0,215; 0,17; 0,143; 0,1; 0,0712; 0,0358). В целом такая методика сокращает цикл обучения системы.

2. Устанавливаются начальные значения 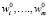весовых векторов всех персептронов, например (0,0,…,0).

3. Устанавливается множество желаемых выходов Y = {yi,…,yN}.

4. Вычисляется решающая функция на выходе нейрона di(х) = (w, хi).

5. Вычисляются значения, s_i = sgn((w, хi)) для всех (хi, yi), и если si = yi, то алгоритм завершается, в противном случае осуществляется поправка весового вектора по правилу

=

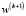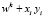
и осуществляется переход к пункту 4.

Пример – применение алгоритма Хебба для обучения одного нейрона классифицировать задачи численных методов

Пусть требуется настроить нейрон на распознавание образов из семи классов, т.е. для заданного множества векторов обучающей выборки Ξ = [хi,…,х7], где х1 = (1,1,1,1,1,1,1)∈Ω1, х2 = (0,1,1,1,1,1,1)∈Ω2, х3 = (0,1,0,1,1,0,0)∈Ω3, х4 = (0,1,1,0,1,1,0)∈Ω4, х5 = (0,0,0,0,1,1,0)∈Ω5, х6 = (0,0,1,0,0,0,0)∈Ω6, х7 = (0,0,1,1,1,1,1)∈Ω7, данную обучающую выборку получили в приведенном примере 2 в работе [1] и проранживали их по значению весового вектора w0 = (0,25; 0,215; 0,17; 0,143; 0,1; 0,0712; 0,0358), в результате получилась обучающая выборка с очередностью, установленной в следующем порядке Ξ = [x1, x2, x3_7, x4, x5_3, x6_5, x7_6] (см. таблицу), требуется так настроить синапсы этого нейрона, чтобы он давал на выходе правильные отклики при предъявлении сети векторов обучающей выборки. Эталонным выходом сети должно быть значение yi = 1, если х_i∈Ω1, и y_i = –1, если х_i∉Ω1. Таким образом, имеем множество Y = {yi,…,yN} = {1, –1, –1, –1, –1,-1, –1} эталонных откликов нейрона. Будем считать, что, входные сигналы являются биполярными, т.е. хi = (х_ij), х_ij∈{–1, 1}, а в качестве функции нейронов используется функция сигнума sgn(t), (функция сигнума равняется 1, если t > 0, и 0, если t ≤ 0). Применительно к обучению одного нейрона правило Хебба формируется следующим образом: если нейрон правильно классифицирует вектор, то порог синоптических связей снижается пропорционально этому вектору [3].

Таким образом, выполнением последовательности действий алгоритма обучения, представленная на рис. 1 с начальным нулевым весовым вектором: w0 = (0,0,0,0,0,0,0) (таблица), получаем следующий результат обучения (таблица).

В таблице ячейки первой строки указывают на шаг итерации. Во второй строке пересчитываются элементы обучающей выборки, в следующих семи строках записаны коэффициенты весового вектора wk, в следующей строке записан результат вычислений скалярных произведений (wk, хi), в предпоследней строке проверяется условие останова найденного весового вектора w, вычисляются значения si = sgn((w, хi)). Если si = yi для всех 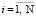, то алгоритм прекращает свою работу, в противном случае – переход к пункту 2. В последней строке знак «+» означает, что вектор классифицировался правильно и коррекцию делать не нужно, а знак «–» означает наоборот. После семи подряд идущих правильных классификаций алгоритм завершает свою работу, в результате получаем требуемый весовой вектор w = (1,0,0,0,0,0,0)T.

На рис. 3 приведен скриншот интерфейса разработанного программного обеспечения для обучения системы с помощью нейронной сети (блок-схема, рис. 1). Через этот интерфейс вводятся входные параметры, т.е. векторы признаков объекта с булевыми переменными и начальные веса, а также, в некоторых случаях оказывается целесообразным задать итерации. Это делается потому, что иногда процесс обучения продолжается очень долго и ограничение на число итераций мы определяем по системе «уровень (шаг)» завершения обучения, даже если искомый весовой вектор не найден. Через этот же интерфейс система сообщает результат обучения, т.е. текущие весовые векторы в каждом шаге обучения и искомый весовой вектор.

В ходе реализации алгоритма обучения Хебба минимизируется следующий функционал

.

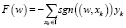Его минимальное значение будет равно (-m), где m – количество классов, и равно 7. Следовательно

F(w) = –((sgn((w, x1))y1) + (sgn((w, x2))y2) + + (sgn((w, x7))y7) + (sgn((w, x3))y4) + + (sgn((w, x3))y3) + (sgn((w, x5))y5) + + (sgn((w, x6))y6)))) = –((1*1) + (–1*–1) + + (–1*–1) + (–1*–1) + (–1*–1) + + (–1*–1) + (–1*–1)) = = –(1 + 1 + 1 + 1 + 1 + 1 + 1 + 1) = – 7.

Это функция заменяется ее «гладкой аппроксимацией» – функцией гиперболического тангенса th(t), получим функционал

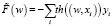= = –(((th(w, х1))*y1) + ((th(w, х2))*y2) + + ((th(w, х7))*y7) + ((th(w, х4))*y4) + + ((th(w, х3))*y3) + ((th(w, х5))*y5) + + ((th(w, х6))*y6)) = (0,7616),

что позволяет при необходимости уточнить положение минимума.

Результат обучения с начальным нулевым весовым вектором

Рис. 3. Скриншоты системы (нейронной сети)

Заключение

В работе были достигнуты следующие результаты:

• Построена математическая модель распознавания образов для SMART-образовательных систем.
• Разработано программное обеспечение для реализации алгоритма обучения и распознавания.
• Приведен пример распознавания и классификации задач из предметной области учебной дисциплины «Численные методы».

В заключение следует отметить, что данная работа является продлением работы [1], в которой приведены входные данные задачи распознавания и подробнее о таблице (таблица). Несмотря на то, что представленные материалы носят образовательный характер, можно отметить, что предложенный алгоритм можно использовать для решения задач большой размерности, что является их преимуществом перед множеством известных простых методов классификации.