В абсолютном большинстве публикаций и по экономике предприятия и, в частности, в работах [2, 3, 7–10] точку безубыточности (критический объем производства) предполагается определять для однономенклатурного производства, исходя из условия покрытия маржинальным доходом только условно-постоянных затрат производственной деятельности:
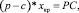 (1)
(1)
где p – цена реализации единицы продукта; c – удельные переменные затраты;
PC – условно-постоянные затраты;
xкр – критический объем производства.
Если реальный объем xр производства выше критического (xр > xк), то предприятие формирует валовой доход величиной (p – c)* xр – PC, в противном случае чистый убыток составит величину PC – (p – c)* xр [7, с. 368; 10, с. 91; 11, с. 68].
В системе учета и планирования затрат директ-костинг соотношение (1) играет фундаментальную роль. Оно позволяет на основе простейших расчетов определить запас финансовой прочности производственной сферы предприятия как функции объема производства, условно – постоянных затрат (эндогенный параметр) и удельного маржинального дохода (экзогенный параметр) [3, с. 64]:
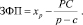 (2)
(2)
Несложно также определить точку безубыточности для монопродуктового, но многоассортиментного предприятия (например, предприятие агросферы или деревообработки). В ряду выпускаемых таким предприятием продуктов 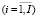 выделяют базовый xб и к нему «привязывают» объемы продукции другой номенклатуры с использованием следующего основного соотношения многоассортиментного предприятия:
выделяют базовый xб и к нему «привязывают» объемы продукции другой номенклатуры с использованием следующего основного соотношения многоассортиментного предприятия:
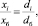 (3)
(3)
где xi, xб – объемы производства соответственно i-го 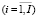 и базового изделий;
и базового изделий;
di, dб – доли в общем объеме выпускаемой продукции (в натуральном выражении) соответственно i-го и базового изделий.
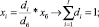 (4)
(4)
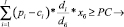
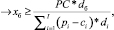 (5)
(5)
где PC – условно-постоянные затраты многоассортиментного предприятия.
Рассмотрим постановку задачи определения критического объема производства для многопродуктового предприятия (общий случай) с учетом риска отклонения доходности изделий производственной программы от планируемых значений (постановка задачи выбора оптимального варианта производственной деятельности предприятия с учетом рыночного риска приведена в работе М.А. Перцевой [5, с. 10]).
Запишем модель многономенклатурного производства в следующем виде:
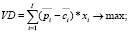 (6)
(6)
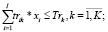 (7)
(7)
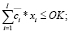 (8)
(8)
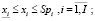 (9)
(9)
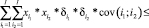
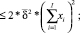 (10)
(10)
 (11)
(11)
где VD – значение валового дохода (критерий в рассматриваемой модели «затраты – выпуск»);
I – число изделий производственной программы;
i, i1, i2 – индекс изделий производственной программы;
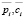 – средние за наблюдаемый период соответственно рыночная цена и удельные переменные затраты на производство i-го изделия;
– средние за наблюдаемый период соответственно рыночная цена и удельные переменные затраты на производство i-го изделия;
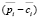 – планируемый удельный маржинальный доход реализации i-го изделия;
– планируемый удельный маржинальный доход реализации i-го изделия;
K – число технологических операций, учитываемых в модели;
trik – технологическая трудоемкость производства i-го изделия на k-й операции;
Trk – эффективное время работы оборудования на k-й операции;
OK – оборотный капитал, авансируемый в покрытие переменных затрат производственной деятельности;
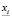 – минимальный (технологически обоснованный) объем производства i-го изделия;
– минимальный (технологически обоснованный) объем производства i-го изделия;
Spi – рыночный спрос на i-ое изделие;
δi – дисперсия маржинального дохода продукции i-го вида за период наблюдения;
cov(i1; i2) – ковариация доходностей продукции с индексами i1 и i2 за период наблюдения;
 – пороговое (максимально допустимое) значение риска производственной программы.
– пороговое (максимально допустимое) значение риска производственной программы.
Экзогенными параметрами модели (6)–(11) являются параметры, определяемые рыночной конъюнктурой: 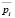 ,
, 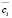 , Spi. Эндогенными (управляемыми) параметрами являются:
, Spi. Эндогенными (управляемыми) параметрами являются: 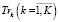 , OK,
, OK,  . Для фиксированных значений экзогенных параметров решение оптимизационной задачи (6)–(11) – вектор
. Для фиксированных значений экзогенных параметров решение оптимизационной задачи (6)–(11) – вектор 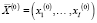 – позволяет определить финансовый результат производственной сферы предприятия как значение критерия
– позволяет определить финансовый результат производственной сферы предприятия как значение критерия 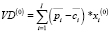 , зависящее от заданной комбинации управляемых параметров
, зависящее от заданной комбинации управляемых параметров 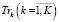 , OK,
, OK,  (так как неравенства – ограничения (7), (8), (10) равнонаправлены, то можно утверждать, что VD(0) монотонно возрастает по каждому управляемому параметру).
(так как неравенства – ограничения (7), (8), (10) равнонаправлены, то можно утверждать, что VD(0) монотонно возрастает по каждому управляемому параметру).
Точка безубыточности многономенклатурного производства определяется из условия
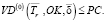 (12)
(12)
Для многономенклатурного предприятия соответствующая критическому уровню производства производственная программа 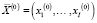 определяется как решение задачи (6)–(11) с критерием, значение которого удовлетворяет условию (12).
определяется как решение задачи (6)–(11) с критерием, значение которого удовлетворяет условию (12).
Кратко остановимся на численном алгоритме решения нелинейной дискретной задачи большой размерности (6)–(11). Известно, что эта задача относится к NP – полным, отличающимися отсутствием универсальных численных алгоритмов поиска оптимального решения [4, с. 476]. По этой причине прибегают к алгоритмам, учитывающим специфику критерия и/или системы ограничений, а также особенности математической формализации задачи.
Рассмотрим модель выпуклого (в данном случае, квадратичного) программирования (6)–(10) в непрерывной постановке: ограничение (11) целочисленности оптимального решения заменяется на ограничение неотрицательности переменных xi:
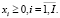 (11')
(11')
Заметим, что и функционал (6), и ограничений (7)–(10), (11') задаются выпуклыми, дважды дифференцируемыми функциями, а следовательно, необходимым условием оптимальности точки 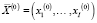 является выполнение условий экстремума в этой точке соответствующей модели (6)–(10), (11') функции Лагранжа
является выполнение условий экстремума в этой точке соответствующей модели (6)–(10), (11') функции Лагранжа 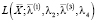 :
:
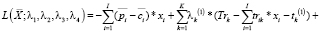
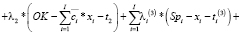
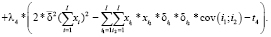 (13)
(13)
В силу отмеченной выше специфики рассматриваемой модели, заключающейся в выпуклости области допустимых решений (удовлетворяющих равнонаправленным ограничениям (7)–(10)) и линейной форме критерия (6), можно утверждать, что экстремум функции Лагранжа (13) определяет единственное оптимальное решение задачи (6)–(10), (11').
Для его поиска, учитывая выпуклость множества допустимых решений, можно предложить следующий численный метод, ранее использованный в работе М.А. Халикова [6, с. 290] и более поздних работах его учеников: М.А. Перцевой [5, с. 14] и Д.А. Безухова [1, с. 12].
Определим базисные решения системы линейных неравенств (7)–(9), удовлетворяющие дополнительному условию (7): 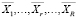 , где R – число отобранных решений (планов), а m – индекс плана. Пусть μr – интенсивность (вес) плана r в оптимальной производственной программе, получаемой простым объединением опорных (базисных) планов:
, где R – число отобранных решений (планов), а m – индекс плана. Пусть μr – интенсивность (вес) плана r в оптимальной производственной программе, получаемой простым объединением опорных (базисных) планов:
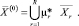 (14)
(14)
Набор весов {μr} найдем как решение следующей задачи линейного программирования:
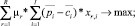 (15)
(15)
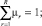 (16)
(16)
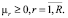 (17)
(17)
Дискретизацию полученного решения 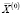 непрерывной задачи (14)–(17) проведем с использованием алгоритма локальной оптимизации, предложенного в цитируемой работе М.А. Халикова [5]. Идея метода заключается в поиске методом последовательных приближений квазиоптимального решения дискретной задачи в ε – окрестности решения непрерывной задачи с последующей оценкой его точности (блок-схема алгоритма представлена на рисунке и соответствует приведенной в работе [1]).
непрерывной задачи (14)–(17) проведем с использованием алгоритма локальной оптимизации, предложенного в цитируемой работе М.А. Халикова [5]. Идея метода заключается в поиске методом последовательных приближений квазиоптимального решения дискретной задачи в ε – окрестности решения непрерывной задачи с последующей оценкой его точности (блок-схема алгоритма представлена на рисунке и соответствует приведенной в работе [1]).
Приведем некоторые комментарии к численному алгоритму, касающиеся метода локальной оптимизации полученного на втором шаге оптимального решения 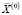 непрерывной задачи (6)–(11). В качестве первого приближения к квазиоптимальному решению целочисленной задачи выбираем вектор с компонентами
непрерывной задачи (6)–(11). В качестве первого приближения к квазиоптимальному решению целочисленной задачи выбираем вектор с компонентами 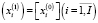 .
.
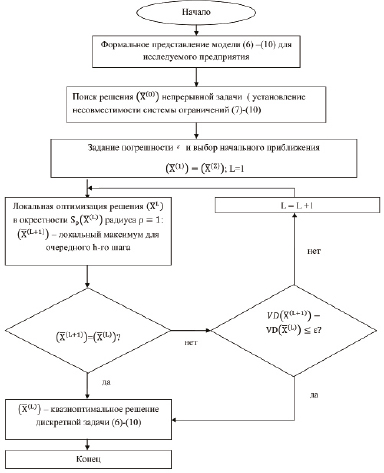
Численный алгоритм поиска квазиоптимального решения дискретной задачи (6)–(10)
Процесс локальной оптимизации связан с перебором точек единичной (в евклидовой метрике) окрестности 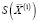 точки
точки 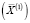 с целочисленными компонентами
с целочисленными компонентами 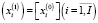 : определяется допустимое решение
: определяется допустимое решение 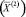 для очередного шага такое, что
для очередного шага такое, что 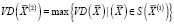 . Если
. Если 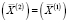 , то полученное на предыдущем шаге решение
, то полученное на предыдущем шаге решение 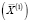 – локальный максимум задачи. Если
– локальный максимум задачи. Если 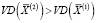 , то переходим к следующему шагу, принимая
, то переходим к следующему шагу, принимая 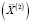 за очередную начальную точку, и т.д. Длительность итеративного процесса зависит от задаваемой исследователем точности ε квазиоптимального решения.
за очередную начальную точку, и т.д. Длительность итеративного процесса зависит от задаваемой исследователем точности ε квазиоптимального решения.
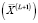 – квазиоптимальное решение задачи (6)–(11), если выполняется неравенство
– квазиоптимальное решение задачи (6)–(11), если выполняется неравенство
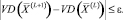
Ценность приведенных моделей и численных методов заключается в решении важной научно-практической задачи определения точки безубыточного производства многономенклатурного производства с учетом рыночного риска. Полученный результат дополняет неоклассическую теорию производства в части совершенствования подходов к оценке эффективности и рыночной устойчивости производственной сферы предприятий корпоративного сектора экономики.
Работа выполнена при поддержке гранта РФФИ р 17-06-00457.



