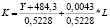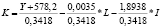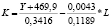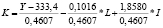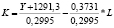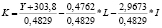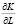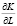Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В настоящем исследовании рассматриваются двух- и трехфакторные связи (зависимости) между основными экономическими показателями регионов России по данным за 2005, 2010 и 2015 гг., публикуемым в справочниках Росстата [1]. Выявление, описание и оценки связей (зависимостей) являются актуальной и важной задачей. Любая задача на выявление связей (зависимостей) для любой однотипной совокупности начинается с постановки задачи, в которой дается формулировка задачи, задаются исходные данные, называются промежуточные и результативные данные, которые должны быть определены, а также определяется форма представления всех информационных документов (таблиц, графиков и др.).

Выявить связи и/или зависимости между показателями экономических объектов означает построить уравнения регрессии, выражающие зависимости результативных показателей от затратно-ресурсных, т.е. рассчитать для них параметры и статистические характеристики [2–4].

Уравнения регрессии могут быть одно- или многофакторными. Параметрами принято называть коэффициенты при показателях-факторах. Статистические характеристики предназначены для оценки тесноты степени корреляционной зависимости результативного показателя от показателей затрат или наоборот, а также приемлемости каждого из уравнений для оценки исследуемой зависимости. Сущность, назначение и методику расчета каждой характеристики можно найти в учебной и научной литературе по эконометрике и статистике [4–6].

В настоящем исследовании мы ограничились оценкой статистических характеристик, рассчитываемых с помощью функций «ЛИНЕЙН» и «ЛГРФПРИБЛ» из MS Excel.

В табл. 1 приведены параметры и характеристики, рассчитанные нами для двух- и трехфакторных уравнений, выражающих зависимость ВРП от 2–3-х ключевых ресурсов. В строках 1–4 этой таблицы приведены параметры, остальные показатели являются статистическими характеристиками.

После расчета параметров целесообразно приводить математическую запись уравнений регрессии. В качестве примера в табл. 2 приведена математическая запись двух- и трехфакторных уравнений регрессии для зависимостей, рассчитанных нами по данным за 2015 г.

Построенные двух- и трехфакторные уравнения требуется анализировать. Для этого следует определить и проанализировать ряд показателей, в частности предельный эффект, коэффициент эластичности, изокванту и предельные нормы взаимозаменяемости показателей-факторов. Методику определения этих показателей можно найти в учебных и научных публикациях по математическому и компьютерному моделированию [4, 6, 7].

Величины предельных эффектов и коэффициентов эластичности могут быть рассчитаны как для одно-, так и многофакторных уравнений регрессии, а изокванты и предельные нормы взаимозаменяемости показателей-факторов – только для многофакторных. Формулы для расчета предельного эффекта и коэффициента эластичности имеют вид

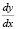– для предельного эффекта;

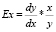– для коэффициента эластичности.

В случае линейной зависимости предельный эффект, а в случае степенной зависимости показателя-фактора равны соответственно параметрам при показателе-факторе.

Разработанный модельно-компьютерный инструментарий позволяет автоматизировать все расчеты и процедуры обработки информации. Однако проведение анализа построенных уравнений регрессии и принятие на их основе управленческих решений являются функциями экономистов-аналитиков, менеджеров и руководителей экономических объектов.

Изоквантой называют множество сочетаний значений показателей-факторов, при которых результативный показатель принимает одно и то же значение. Чтобы найти изокванту, надо: принять Y за константу (Y = const) и выразить один из факторов через остальные [1–3].

Таблица 1

Величины параметров и статистических характеристик для двух- и трехфакторных линейных уравнений регрессии, выражающих зависимости ВРП (Y) от стоимости основных фондов (K), численности занятых в экономике (L) и инвестиций (I)

Таблица 2

Математическая запись двух- и трехфакторных уравнений регрессии для зависимостей ВРП от стоимости основных фондов, численности занятых в экономике и объема инвестиций, построенных по данным федеральных округов за 2015 г.

Например, для Y = b + m1*X1 + m2*X2 изоквантой является

или

.

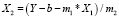Предельная норма заменяемости одного фактора другим позволяет определить, сколько единиц одного фактора требуется для замены одной единицы другого фактора.

Чтобы рассчитать предельные нормы взаимозаменяемости показателей-факторов, надо:

а) найти изокванту;

б) определить частную производную одного фактора по другому, т.е.

,

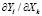где l ≠ k, l и k∈i = 1, 2,…,n [1, 3, 4].

Например, для Y = b + m1*X1 + m2*X2 предельные нормы взаимозаменяемости составляют 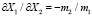и .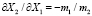

После определения на ПЭВМ предельных эффектов, коэффициентов эластичности, изоквант и предельных норм взаимозаменяемости показателей-факторов задачу по созданию математических и компьютерных моделей, а также информационного обеспечения можно считать решенной.

Совокупность всех формул, необходимых для решения поставленной задачи, называется математической моделью. Рассматриваемая задача является типовой, требующей многократного применения для различных совокупностей данных. Кроме того решение задачи связано с выполнением множества расчетов, т.е. возникает необходимость в создании компьютерной модели с целью перевести на компьютерную основу: во-первых, всех таблично-графических материалов; во-вторых, всех формул; в-третьих, автоматизировать выполнение всех расчетов и процедур обработки информации. Все перечисленные элементы созданные и функционирующие на ЭВМ, можно назвать компьютерной моделью. Такая модель для решения рассматриваемой в настоящем исследовании задачи создана нами в MS Excel.

Разработанный модельно-компьютерный инструментарий позволяет автоматизировать все расчеты процедуры обработки информации. Однако проведение анализа построенных уравнений регрессии, совокупности их различных показателей, а также связей (зависимостей) между показателями и принятых на их основе управленческих решений является функцией аналитиков, менеджеров и руководителей экономических объектов.

Анализ уравнений регрессии начинается, как правило, с анализа статистических характеристик, наиболее важными из которых являются: стандартная ошибка для зависимой переменной (sey), индекс детерминации (r2), критерий Фишера (F) и средняя ошибка аппроксимации (A, %) [3, 4, 7].

Сформулируем аналитические выводы по величинам индексов детерминации, средней ошибки аппроксимации и других статистических характеристик.

– по двух- и трехфакторным уравнениям, выражающим зависимость ВРП от стоимости основных фондов, численности занятых в экономике и объемов инвестиций (Y от K, L и Y от K, L, I) степень тесноты корреляции является очень высокой (r² > 0,92), исключение составляет r2 для зависимостей показательного и степенного видов (Y от K, L) за 2010 и 2015 гг. (r² ≈ 0,88);

– по величинам средней ошибки аппроксимации (измеряется в %) все двух- и трехфакторные уравнения показательного и степенного вида получили оценку «хорошо» (А менее 10 %) весьма близко к оценке «хорошо» и уравнения линейного вида, для которых А = (11,0 – 15,7 %).

Таблица 3

Величины предельных эффектов и коэффициентов эластичности для двух- и трехфакторных уравнений регрессии, выражающих зависимость ВРП регионов РФ в разрезе федеральных округов от трех ключевых ресурсов за 2005, 2010, 2015 гг.

Примечание. K – стоимость основных фондов; L – численность занятых в экономике; I – инвестиции.

Таким образом, все построенные двух- и трехфакторные уравнения регрессии, выражающие линейные, показательные и степенные виды зависимостей, оказались приемлемыми для описания и оценки исследуемых связей (зависимостей).

В соответствии с эконометрической теорией после оценки приемлемости уравнений принято проводить оценку параметров регрессий, а также ряда показателей, которые могут быть определены на основе построенных уравнений регрессии и их параметров [2, 3, 7].

Прежде всего, проанализируем величины двух наиболее ценных из показателей, которые могут быть определены по уравнениям регрессии: предельных эффектов и коэффициентов эластичности. Особый интерес предельный эффект представляет в случае линейных, а коэффициент эластичности – в случае степенных видов уравнений регрессии, которые приведены в табл. 3.

На основе данных табл. 3 можно сформулировать ряд выводов, в частности следующие:

– по линейным двухфакторным уравнениям регрессии (Y от K, L) предельный эффект от использования основных фондов уменьшился почти в 2 раза, а использование численности увеличилось (с – 0,0043 в 2005, до 0,1189 в 2010 и до 0,3731 руб. в 2015 г.);

– по линейным трехфакторным уравнениям (Y от K, L, I) предельный эффект использования основных фондов и численности имел рост в каждые пять лет, а эффект использования инвестиций в 2005 г. был положительным, в 2010 г. он оказался отрицательным (–1,8580), а в 2015 снижение оказалось еще более высоким (до – 2,9673 %);

– по степенным двухфакторным уравнениям регрессии для зависимости Y от K, L коэффициент эластичности основных фондов каждые пять лет заметно (с 1,24 до 0,70 %) уменьшился, а численности – вырос (с 0,002 до 0,430 %);

– по степенным трехфакторным уравнениям регрессии (Y от K, L, I) коэффициент эластичности основных фондов снизился (с 1,14 до 0,86 %), численности занятых в экономике вырос (с 0,01 до 0,46 %); эластичность инвестиций в 2005 г. была положительной и составила 0,10 %, в 2010 г. увеличилась до 0,27 %, но в 2015 г. уменьшилась и даже стала отрицательной (–0,23 %).

Предельные эффекты и коэффициенты эластичности во всех других случаях представляют собой переменные величины.

Сами по себе изокванты уже представляют аналитический интерес, поскольку позволяют определить различные сочетания величин показателей-факторов, при которых может быть достигнута одна и та же величина результативного (зависимого) показателя.

Так, например, в 2005 г. объем ВРП (Y), стоимость основных фондов (K), численность занятых в экономике (L) и объем инвестиций (I) по Республике Дагестан составили: 538,3 млрд руб., 1213 млрд руб., 1011,7 млрд руб. и 231,1 млрд руб.

Для группы средних регионов (куда входит Республика Дагестан) по данным за 2005 г. формула изокванты имеет вид:

а) для двухфакторных уравнений, выражающих зависимость Y от K и L:

;

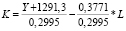б) для трехфакторных уравнений Y от K, L и I:

.

Для Республики Дагестан самым важным ресурсом является численность занятых в экономике, которая в 2015 г. составила 1011,7 тыс. чел. Если в вышеприведенную формулу изокванты K = f(L) подставить значение численности за 2015 г., то величина K будет равна

.

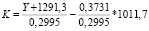Откуда, выполнив соответствующие расчеты, получим формулу изокванты: K = 3,3389*Y – 1273,8.

Если принять за Y = const величину ВРП за 2015 г. (т.е. 538,3 млрд руб.), то K будет равна 523,5 млрд руб. Задавая для показателя-фактора L другие числовые значения, можно получить совокупность значений K и L, при которых ВРП (Y) будет принимать одну и ту же величину 538,3 млрд руб.

Если в вышеприведенную формулу изокванты K = f(L, I) для трехфакторного уравнения регрессии подставить значения численности занятых в экономике за 2015 г., то величина K будет равна

.

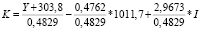Выполнив соответствующие расчеты, получим

K = 2,0708*Y – 997,7 + 6,1448*I.

Если ВРП (Y) принять равной ее величине за 2015 г. (538,3 млрд руб.), то формула изокванты примет вид K = 117,1 + 6,1448*I.

Пусть объем инвестиций равен их величине за 2015 г. (т.е. 231,1 млрд руб.). Подставляя это значение инвестиций (I) в последнюю формулу K = f(I), получим численную величину для стоимости основных фондов K = 1537,1 млрд руб.

Таким образом, согласно рассмотренному примеру объем ВРП, равный его величине за 2015 г. можно было получить и при следующем сочетании значений K, L и I: K = 1537,1 млрд руб.; L = 1011,7 тыс. чел.; I = 231,1 млрд руб.

Нет необходимости приводить математическую запись изоквант для всех построенных уравнений регрессии. Поэтому в табл. 4 приведена математическая запись изоквант только для линейных уравнений.

По формуле изокванты можно определить показатели, которые называются предельными нормами взаимозаменяемости показателей-факторов. Показатели-факторы, включаемые в многофакторные уравнения регрессии, являются, как правило (если они правильно выбраны), взаимозаменяемыми.

В нашем случае нет сомнения во взаимозаменяемости двух главных ресурсов региональной экономики: стоимости основных фондов (K) и численности занятых в экономике (L). Очевидна (хотя и в меньшей степени) взаимозаменяемость численности занятых в экономике (L) и объемов инвестиций (I). А вот вопрос, взаимозаменяемы ли основные фонды (K) и инвестиции (I), не является очевидным.

С математической точки зрения все факторы, включаемые в уравнения регрессии, являются взаимозаменяемыми. Но в эконометрических уравнениях не всегда показатели-факторы являются взаимозаменяемыми. Дело в том, что в одно и то же многофакторное уравнение регрессии нельзя включать зависимые между собой показатели-факторы. Но в экономике большинство показателей в той или иной степени взаимосвязаны (взаимозависимы). Поэтому трудно найти показатели-факторы, вовсе независимые друг от друга.

Таблица 4

Математическая запись изоквант для двух- и трехфакторных уравнений регрессии, выражающих зависимости ВРП (Y) от стоимости основных фондов (K), численности занятых в экономике (L) и инвестиций (I) по данным регионов РФ за 2005, 2010 и 2015 гг.

Согласно эконометрической теории корреляция между включаемыми в одну и ту же модель показателями-факторами должна быть максимально низкой. Отметим также, что понятия «связь» и «зависимость» в экономике не являются синонимами. «Связь» – понятие более широкое. «Зависимость» всегда одновременно является и связью, но связь не всегда означает зависимость. В нашем случае стоимость основных фондов и численность занятых – это действительно взаимозаменяемые ресурсы. Стоимость основных фондов и численность не зависят друг от друга, но они могут быть корреляционно связанными. Регионы, имеющие большие величины стоимости основных фондов, как правило, имеют и большую величину численности занятых. То же примерно можно сказать и относительно показателей-факторов численности занятых в экономике и объема инвестиций.

Иначе обстоит дело с показателями стоимости основных фондов и инвестиций. Дело в том, что большая часть инвестиций в виде капитальных вложений направляется на обеспечение прироста и/или обновления основных фондов. Из этого следует, что стоимость основных фондов зависит от инвестиций (естественно, эта зависимость корреляционная).

Особый аналитический интерес представляют предельные нормы взаимозаменяемости для уравнений регрессии линейного и показательного видов. В этом случае предельные нормы выражаются численными величинами. Предельные нормы взаимозаменяемости факторов для других нелинейных уравнений являются переменными величинами, выражаемыми формулами. В качестве примера ниже приведем величины предельных норм взаимозаменяемости для двухфакторных уравнений регрессии Y = f(K, L) соответственно для линейного, показательного и степенного видов. Формулы изоквант имеют вид:

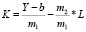– для линейного уравнения;

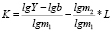– для показательного уравнения;

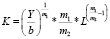– для степенного уравнения.

Предельные нормы для этих изоквант будут иметь вид:

а) для линейного уравнения

; ;

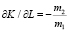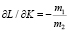б) для показательного уравнения

; ;

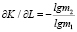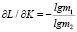в) для степенного уравнения

;

.

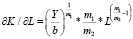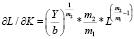Являются ли показатели-факторы взаимозаменяемыми или нет, можно определить по знакам для предельных норм взаимозаменяемости. Если предельная норма взаимозаменяемости имеет знак (–), то показатели-факторы являются взаимозаменяемыми, если знак положителен, то факторы не являются взаимозаменяемыми. В табл. 5 приведены величины предельных норм взаимозаменяемости ресурсных показателей K, L и I для уравнений линейного и показательного видов.

Таблица 5

Величины предельных норм взаимозаменяемости ресурсных показателей K, L и I для уравнений линейного вида

Как видно из табл. 5, в двухфакторных линейных уравнениях регрессии, выражающих зависимость ВРП от стоимости основных фондов (K) и численности занятых в экономике (L) по данным за 2005 г. основные фонды и численность работников не являются взаимозаменяемыми, по данным за 2010 и 2015 гг. эти два ресурса являются взаимозаменяемыми. При этом в 2010 г., чтобы заменить 1 тыс. чел. численности занятых в экономике, требовалось 0,3 млрд руб. основных фондов; в 2015 г. на 1 тыс. чел. требовалось 1,2 млрд руб. основных фондов. То есть отдача от основных фондов снизилась почти в 4 раза. Это обусловлено, с нашей точки зрения, двумя причинами: с одной стороны, физическим и моральным износом основных фондов экономики; с другой стороны, относительным сокращением численности занятых в экономике и ростом их квалификационного уровня.

Согласно трехфакторным уравнениям, основные фонды и численность занятых в экономике во все три рассмотренных периода (2005, 2010 и 2015 гг.) оказались взаимозаменяемыми (∂K/∂L имеет отрицательный знак). При этом заменяемость 1 тыс. чел. занятых в экономике работников основными фондами составила в 2005 г. 0,01, в 2010 г. 0,24, в 2015 г. 1,00 млрд руб. Эти цифры также свидетельствуют об ухудшении качества основных фондов (моральный и физический износ).

Как известно, стоимость основных фондов в значительной степени зависит от объемов инвестиций в экономике, поскольку большая их часть в виде капитальных вложений направляется на прирост и обновление основных фондов. С этой точки зрения стоимость основных фондов и инвестиций не являются взаимозаменяемыми ресурсами. Это видно и из величин ∂K/∂I, которые оказались (как и должно быть) положительными.

Аналогичной оказалась ситуация и с предельными нормами взаимозаменяемости численности занятых в экономике и объемов инвестиций: в 2005 г. 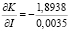; в 2010 и 2015 гг. знаки величины ∂K/∂I оказались плюсовыми, свидетельствующими об отсутствии взаимозаменяемости этих ресурсов. Напомним в этой связи, что часть объема инвестиций используется на подготовку и повышение квалификации работников занятых в экономике, что является аргументом, подтверждающим отсутствие взаимозаменяемости численности занятых и инвестиций.