В отечественной литературе, посвященной вибрации и шуму машин и производств текстильной промышленности, основное внимание уделяется хлопчатобумажным [1], льняным и др. Динамическим расчетам механизмов прядильных, ткацких, трепальных и др. машин посвящено множество научных трудов различных авторов.
Вместе с тем внимание исследователей к изучению оборудования и технологий металлоткачества продолжает оставаться недостаточным. По нашим сведениям за период с 1970 по 1996 гг. во всем мире (исключая Российскую Федерацию) было опубликовано всего лишь 18 работ, затрагивающих металлоткачество и производство трикотажа из металлической проволоки. Из них пять публикаций в Германии, четыре – в США, по три – во Франции и в Англии, по одной – в Бельгии, Индии, Чехии. Десять – являются патентами. Имеется также чуть более 30 публикаций по металлическим и металлизированным волокнам и мононитям [2]. А работ, посвященных исследованию вибрационных и шумовых характеристик металлоткацкого производства, не встретилось ни одной.
Наиболее распространенные ткацкие станки для выработки тканой металлической сетки имеют заправочную ширину 100 см. При проектировании металлоткацких станков с широкой заправочной линией возникает необходимость исследования уровня вибрации и шума, создаваемого ремизной рамой, являющейся одним из основных источников возникновения этих явлений станка в целом. Вибрации, возникающие в процессе работы в этом звене, могут значительно влиять на протекание технологического процесса, а шум оказывает негативное действие на обслуживающий персонал.
Важнейшей характеристикой колебательного процесса (шума, вибрации) является его частотный спектр. Разложение сложного колебательного процесса на простейшие составляющие называют частотным анализом процесса, а величину, указывающую на характер распределения параметров по частотному диапазону, – его частотным спектром. Как правило, машины имеют смешанный спектр, состоящий из непрерывной части, внутри которой располагаются достаточно четко выраженные гармоники. Непрерывный спектр обуславливается различными случайными и неустановившимися процессами, а дискретный – постоянно действующими причинами (силами), например возникновение вибрации с определенным частотным спектром может быть вызвано инерционными силами [1].
В работах [3, 4] решены предшествующие задачи необходимые для достижения цели данного исследования – исследование вибрации и шума ремизной рамы металлоткацкого станка СТМ-4-130. В работе [3] для изучения работы механизма с учетом колебательных явлений разработаны динамические модели, в соответствии с которыми предложены и решены математические модели задач о собственных крутильных колебаниях валов, произведены расчеты собственных частот по указанным моделям, установлено, что механизм привода челноков работает вне зоны резонанса, определяемой паспортными режимами эксплуатации станка. В работе [4] для определения упругих деформаций ремизной рамы предложены динамические модели различного типа, решена задача о вынужденных колебаниях ремизной рамы, расчет выполнен двумя методами, которые дают близкие по значению результаты, что говорит об адекватности предложенных моделей.
В результате [4] определена зависимость (1) значения упругих деформаций, для разработанной модели ремизной рамы (рис. 1) в различных сечениях в зависимости от закона движения, упруго-инерционных характеристик рамы, технологических параметров и времени.
На рис. 1 приняты следующие обозначения:
с1 и с2 – коэффициенты жесткости;
Т – натяжение нитей основы;
m1 и m2 – сосредоточенные массы;
Kn – коэффициент пропорциональности между натяжением нитей основы, деформацией нижней планки и перемещением ремизной рамы;
µ – интенсивность распределенной массы системы;
f(t) – закон движения ремизной рамы;
l – длина нижней планки ремизной рамы;
EY – жесткость нижней планки на изгиб.
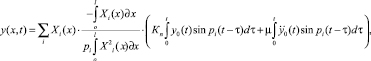(1)
где pi – собственные частоты системы;
Xi(x) – собственные формы системы;
i – индекс собственной частоты (формы) системы;
y0(t) – кинематическое перемещение рамки на рассматриваемой фазе движения;
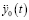– возмущающая функция (аналог линейного ускорения точек крепления упругих связей) на рассматриваемой фазе движения.
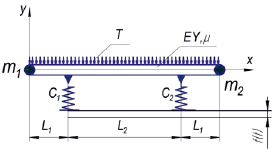
Рис. 1. Динамическая модель ремизной рамы
Параметры вибрации и шума зависят как от мощности самого источника и расстояния до него, так и от акустических свойств окружающего пространства. Поэтому основными характеристиками излучаемого механизмом шума являются мощность и виброскорость, характеризующие общую энергию излучения механизма.
Мощность излучаемого колеблющимся телом (или участком тела) шума зависит от формы колебаний, геометрии тела и пропорциональна квадрату средней виброскорости на поверхности излучателя.
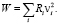(2)
Размерный коэффициент пропорциональности R между звуковой мощностью и квадратом амплитуды виброскорости на поверхности излучателя называется акустическим сопротивлением излучателя.
По результатам исследований, указанных в работе [1], основными типами излучателей в ткацком станке являются точечные излучатели (монополи), акустическое сопротивление которых можно определить как
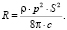(3)
Тогда мощность излучения определится как
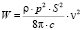, (4)
где ρ – плотность среды, кг/м3;
p – собственная частота колебаний;
Sn – площадь поверхности излучения планки, м2;
c – скорость звука в среде, м/с;
v – виброскорость, м/с;
В нашем случае значение виброскорости можно получить, вычислив производную по времени от выражения (1)
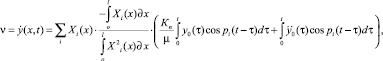(5)
а действующее (среднее) значение виброскорости зависимостью
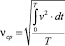, (6)
так как эта величина есть среднеквадратическое мгновенных значений скорости V за время усреднения T.
Принимая для нашего случая в качестве модели излучателя точечный источник, необходимо определить среднюю скорость по поверхности планки. Для этого вычислим выражение
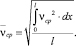(7)
Уровни интенсивности звука и вибрации можно определить через величины W и ν следующими зависимостями:
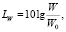(8)
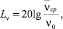(9)
где W0, ν0 – значения нулевых порогов интенсивностей звуковой мощности и виброскорости соответственно [5].
Производим расчеты, принимая в качестве исходных данных следующие значения физических величин: ρ = 1,2 кг/м3, S = 0,0138 м2, с = 340 м/с, T = 0,21c, W0 = 10-12Вт, ν0 = 5·10-6 см/с.
Результаты расчетов по приведенной выше методике сведены в таблице.
На рис. 2 приведены зависимости среднего значения виброскорости на поверхности планки от собственных частот модели
Зависимости интенсивностей вибрации и шума от собственных частот системы изображены на рис. 3.
Полученные результаты позволяют сделать следующие выводы. Пиковые значения вибрации и шума ремизной рамы приходятся на октавные полосы со среднегеометрическими частотами в 63, 250 Гц, возбуждаемые на первой и третьей собственных частотах.
Сравнивая (условно) с допустимой нормой уровней шума в производственных помещениях [1] для октавной полосы 63Гц – 99Дб, для октавной полосы 250 Гц – 86Дб. Таким образом, можно сказать, что уровень шума во всех октавных полосах лежит в допустимых пределах.
Вибрация относится к факторам, обладающим высокой биологической активностью. Выраженность ответных реакций обусловливается главным образом силой воздействия и биомеханическими свойствами человеческого тела как сложной колебательной системы [6].
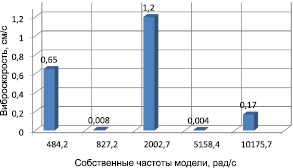
Рис. 2. Значения среднего значения виброскорости на поверхности планки в зависимости от собственных частот модели
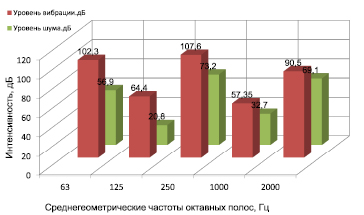
Рис. 3. Значения интенсивностей вибрации и звуковой мощности в октавных полосах
Результаты расчетов интенсивностей звуковой мощности и вибрации
|
Октавная полоса, Гц |
Собственная частота, pi рад/с – Гц |
Vср, см/с |
Lv, дБ |
W, Вт |
Lw, дБ |
|
63 |
p1, 484,2 – 77,01 |
0,65 |
102,3 |
1,76·10-7 |
56,9 |
|
125 |
p2, 827,2 – 131,65 |
0,008 |
64,4 |
1,15·10-10 |
20,8 |
|
250 |
p3, 2002,7 318,69 |
1,2 |
107,6 |
1,52·10-5 |
73,2 |
|
500 |
– |
– |
– |
– |
– |
|
1000 |
p4, 5158,4 – 820,97 |
0,004 |
57,4 |
9,50·10-10 |
32,7 |
|
2000 |
p5, 10175,7 – 1619 |
0,17 |
90,5 |
7,13·10-6 |
69,1 |
Параметры колебательного процесса в зоне взаимодействия и его время являются определяющими параметрами, влияющими на развитие болезней, связанных с вибрацией. Ключевыми факторами при этом являются частоты, формы и амплитуды колебаний, направление действия вибрационных сил, упругих свойств тканей, наличие резонансных явлений и многих других условий.
По характеру воздействия различают общую и локальную вибрации. При общей вибрации происходит сотрясение всего организма. При локальной вибрации происходит сотрясение отдельных частей тела, например кистей рук. Наиболее опасным является первый тип [7].
В нашем случае колебания, возбуждаемые по третьей форме, превышают допустимые пределы по значениям виброскорости и уровню интенсивности общей вибрации (для октавной полосы 63 Гц – 0,2 см/с и 92 дБ)[1]. Уровни и виброскорости локальной вибрации лежат в допустимых пределах (для октавной полосы 63 Гц – 1,4 см/с и 109 дБ, для октавной полосы 250 Гц – 1,4 см/с и 109 дБ) [5].
Выводы
1. Разработана методика теоретического анализа звуко- и виброактивности механизма ткацкого станка.
2. Получены спектры мощности звуко- и виброизлучения для ремизной рамы металлоткацкого станка. Установлено, что максимальные уровни шума и вибраций лежат в пределах октавных полос со среднегеометрическими частотами 63, 250, 2000 Гц.
3. Установлено, что определенные уровни шума во всех октавных полосах лежат в допустимых пределах.
4. Вибрации, возбуждаемые колебаниями по первой и третьей формам, превышают допустимые пределы по значениям виброскорости и уровню интенсивности как общей, так и локальной вибраций.