В настоящее время происходит интенсивное развитие и усложнение банковских информационных систем и технологий, также наблюдается тенденция к сокращению релизного цикла, повышение скорости разработки и обеспечение возможности выпуска релиза в любой момент. Растёт популярность гибких методологий (Agile) [1], а также методологии DevOps (development and operations) [2] среди российских банков и их технологических подразделений. В условиях сокращения скорости вывода новых продуктов на рынок и повышения гибкости внедрений (release anytime) банки сталкиваются с проблемой поддержки текущих показателей надёжности автоматизированных систем и минимизации операционных IT-рисков. По этой причине управление релизным циклом банковского программного обеспечения не может рассматриваться отдельно от соответствующих технологических рисков, которые может привнести установка нового релиза.
Операционный IT-риск – это риск ущерба текущей деятельности банка в виде убытка или недополученного дохода, вызванный используемыми информационными технологиями и IT-процессами [3]. Примерами последствий инцидентов операционного IT-риска могут служить неверно рассчитанные платежи по кредитам, сбои в работе карточного процессинга в часы пиковой нагрузки, ошибки при расчете комиссионного вознаграждения банка при переводе денежных средств. Подобные ошибки способны привести к серьёзным денежным и репутационным потерям для различных организаций.
Cогласно методологии ITIL [4] управление IT-релизами – это процесс, отвечающий за планирование и контроль сборки, тестирования и развёртывания релизов, а также за внедрение нового функционала без нарушения целостности существующих IT-сервисов.
В современной литературе по управлению IT-процессами, включая методологию ITIL, слабо отражена проблема интеграции процесса управления релизами и процесса управления рисками. Цель данной статьи заключается в описании основных подходов к управлению IT-рисками в рамках релизного цикла банковского ПО, а также в разработке математической модели прогнозирования операционных IT-рисков перед внедрением новых версий программного обеспечения. При построении математической модели использован аппарат теории вероятностей, математической статистики и методов Монте-Карло. Представленная модель реализована с использованием языка программирования R.
Методы предотвращения реализации IT-рисков
Приведём основные мероприятия и практики, направленные на выявление и предотвращение реализации IT-рисков при внедрении нового функционала ПО, а также на снижение вероятности наступления рискового события либо минимизации его последствий в случае реализации.
- Перед выпуском каждая доработка должна проходить обязательное тестирование. Также должен быть протестирован старый функционал, который мог быть затронут изменениями (регрессионное тестирование). Задача тестирования ПО – проверка соответствия реального и ожидаемого поведения программного обеспечения. Обязательным условием проведения тестирования критичного банковского ПО является развёртывание и использование отдельных тестовых сред [5].
- Пилотирование нового функционала на промышленном контуре без тиражирования на все географические локации, отделения банка или устройства самообслуживания [3]. Данный подход предназначен для проверки работоспособности каждой следующей версии релиза в условиях реальных данных и ведет к уменьшению операционных рисков, а также к сокращению сроков вывода на рынок новых банковских услуг.
- Использование систем мониторинга за сбоями в финансовых транзакциях, а также обеспечение возможности отката нового функционала с промышленного контура в случае обнаружения сбоев.
- Непрерывный сбор статистических данных по инцидентам операционного риска, последующий анализ и выявление типовых рисков, которые имеют сходные сценарии реализации и могут быть предотвращены общими мероприятиями. При функциональном тестировании и при приемо-сдаточных испытаниях каждого релиза рекомендуется проводить тесты, покрывающие типовые риски.
Модель прогнозирования ущерба от IT-инцидентов
Считается, что на начальных фазах жизненного цикла ПО на 1000 строк исходного кода приходится 1–3 ошибки, которые приводят к дефектам вычислительного процесса [6]. Программа, состоящая из нескольких сотен строк, может иметь тысячи альтернативных путей выполнения. По этой причине отделы тестирования сталкиваются с проблемой неосуществимости исчерпывающего тестирования (exhaustive testing). Это означает, что невозможно найти 100 % дефектов в той или иной системе. Однако существует возможность, используя статистические данные, приближенно оценить число пропущенных дефектов и, как следствие, ущерб.
Опишем метод оценки, который базируется на модели Value at Risk (VaR).
Модели VaR, изначально разработанные в конце XX в. для оценки рыночного риска, могут также быть использованы в управлении операционными рисками для расчёта стоимостной меры операционного риска OpVar (Operational Value at Risk) [3].
Определим стоимостную меру операционного риска (operational value at risk, OpVar) IT-релиза t как значение потерь RLt (release losses) от инцидентов операционного риска в данном релизе, которая не будет превышена с вероятностью α.
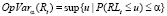 . (1)
. (1)
В формуле (1) множество 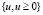 – это множество всех возможных значений ущерба u в рассматриваемом релизе.
– это множество всех возможных значений ущерба u в рассматриваемом релизе.
Потери от операционных рисков – это дискретный во времени случайный процесс, что является фундаментальным отличием OpVar от рыночных моделей VaR, в которых цена актива рассматривается как непрерывный случайный процесс.
Введём понятия интенсивности и критичности операционного риска.
Интенсивность (frequency) риска определим как количество Nt дефектов, привнесенных релизом t, t = 1,2,…, T.
Под критичностью (severity) риска будем понимать величину Li финансовых потерь, которые повлёк за собой дефект i, i = 1,2,…, Nt.
Предположим, что интенсивность риска имеет распределение Пуассона c математическим ожиданием λ, а частные потери от дефекта i (критичность риска) подчинены логнормальному [8] распределению с параметрами μ и σ2:
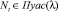 ,
,
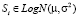 .
.
Также сделаем предположение, что случайные величины Nt и Li являются независимыми.
Совокупные потери за релиз t могут быть рассчитаны по следующей формуле:
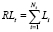 . (2)
. (2)
Функция распределения случайной величины RLt может быть представлена в следующем виде:
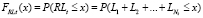 .
.
Вывод точной формулы для 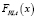 является трудноразрешимой задачей [7], и в данной статье будет предложена модель оценки OpVar, основанная на методе Монте-Карло.
является трудноразрешимой задачей [7], и в данной статье будет предложена модель оценки OpVar, основанная на методе Монте-Карло.
Пусть имеется массив статистических данных по IT-инцидентам для серии релизов. Методом максимального правдоподобия [8] можно оценить математическое ожидание 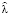 для распределения Пуассона, а также параметры
для распределения Пуассона, а также параметры 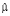 и
и 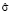 для логнормального распределения:
для логнормального распределения:
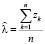 , (3)
, (3)
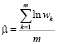 , (4)
, (4)
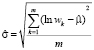 . (5)
. (5)
В формуле (3) 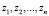 – статистические данные по количеству дефектов на релиз, в формулах (4) и (5)
– статистические данные по количеству дефектов на релиз, в формулах (4) и (5) 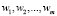 – данные по величине ущерба на дефект (в руб.).
– данные по величине ущерба на дефект (в руб.).
Очевидно, что статистические данные по инцидентам будут отсутствовать на ранних этапах проекта по разработке банковского ПО. Для ПО, которое используется в промышленной эксплуатации больше 3–5 лет, статистика также может отсутствовать или может быть неточной. В таких случаях для прогнозирования параметров интенсивности и критичности операционного риска (то есть параметров 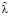 ,
, 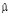 и
и 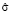 ) следует использовать статистические данные по смежным проектам либо метод экспертных оценок.
) следует использовать статистические данные по смежным проектам либо метод экспертных оценок.
Используя метод Монте-Карло, сгенерируем N случайных величин, распределенных по Пуассону с параметром 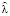 :
: 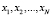 .
.
Затем смоделируем потери, подчиненные логнормальному распределению с параметрами 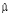 и
и 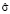 , и, таким образом, получим совокупную матрицу интенсивности и критичности операционного риска (aggregated frequency and severity):
, и, таким образом, получим совокупную матрицу интенсивности и критичности операционного риска (aggregated frequency and severity):
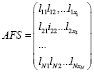 .
.
Заметим, что разные строки матрицы AFS содержат различное число элементов, причём некоторые строки могут не содержать ни одного элемента.
Сложим элементы матрицы AFS по строкам и получим вектор совокупных потерь в разрезе N релизов:
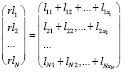 .
.
Упорядочим получившиеся суммы по возрастанию:
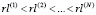 .
.
Для расчёта OpVar найдём номер k*, такой, что 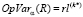 .
.
Исходя из (1) и из того, что все сценарии равновероятны:
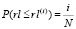 .
.
Отсюда
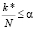 ,
, 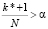 ,
,
иначе 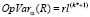 .
.
Поэтому:
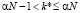 .
.
Окончательно получим, что
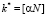 . (6)
. (6)
Также можно рассчитать OpCVar (operational conditional value at risk) – математическое ожидание ущерба при условии, если он превысит значение VaR:
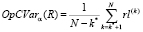 . (7)
. (7)
Расчёт показателя Value at Risk с использованием языка R
Продемонстрируем предложенный алгоритм расчёта OpVar на примере. Пусть имеются статистические данные за 14 релизов банковской автоматизированной системы (таблица), и требуется спрогнозировать потери от IT-инцидентов для внедряемого в настоящий момент релиза 15.
Для оценки параметров 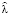 ,
, 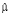 и
и 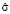 выполним скрипт (рис. 1) на языке программирования R [9].
выполним скрипт (рис. 1) на языке программирования R [9].
Получим:
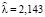 ,
, 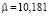 ,
, 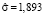 .
.
Рассчитаем показатели OpVar и OpCVar, используя R.
Листинг программы имеет следующий вид:
events_number<-10000 #1. Количество разыгрываемых сценариев
lambda<-fitdist(freq_hist, distr=»pois», method=»mle»)$estimate #2. Параметр λ распределения Пуассона
lnorm_mean<-coef(fitdist(sev_hist, distr=»lnorm», method=»mle»))[1] #3. Параметр μ логнормального распределения
lnorm_sigma<-coef(fitdist(sev_hist, distr=»lnorm», method=»mle»))[2] #4. Параметр σ логнормального распределения
alpha=0.95 #5. Доверительный уровень
k<-floor(alpha*events_number) #6. Параметр k* для расчёта OpVar
freq_sev_matrix<-list() #7. Генерация матрицы AFS (aggregated frequency and severity)
for(i in 1:events_number){
sev_vector <- c();
t<-rpois(1, lambda)
if(t>=1){
for(j in 1:t){
sev_vector<-append(sev_vector, rlnorm(1, meanlog=lnorm_mean, sdlog=lnorm_sigma));
}
}
freq_sev_matrix[[i]]<-sev_vector
}
total_sev_vector <- c(); #8. Вектор из сумм строк матрицы AFS
for(i in 1:events_number){
total_sev_vector<-append(total_sev_vector, sum(freq_sev_matrix[[i]]))
}
sorted_total_sev_vector<-sort(total_sev_vector) #9. Сортировка координат вектора из сумм строк матрицы AFS
var<-sorted_total_sev_vector[k] #10. Расчёт Var/CVar
above_var<-sorted_total_sev_vector[c((k+1):events_number)]
cvar<-mean(above_var)
print(var)
print(cvar)
Статистические данные по IT-инцидентам
|
№ релиза |
Кол-во дефектов |
Ущерб от дефектов, руб. |
|
1 |
4 |
1586,74; 17379,30; 7416,71; 777,15 |
|
2 |
2 |
2863,54; 380513,40 |
|
3 |
2 |
314524; 15612,34 |
|
4 |
1 |
14857,74 |
|
5 |
4 |
141454,40; 97545,28; 3145,53; 6556,40 |
|
6 |
1 |
11428,18 |
|
7 |
4 |
83540,83; 24519,78; 14995,63; 908,42 |
|
8 |
1 |
136772,20 |
|
9 |
2 |
37441,59; 137692,50 |
|
10 |
2 |
22281,86; 1505342 |
|
11 |
0 |
– |
|
12 |
3 |
132279,50; 64807,78; 365711,60 |
|
13 |
1 |
9411,29 |
|
14 |
3 |
176826,20; 4368,12; 7258,91 |
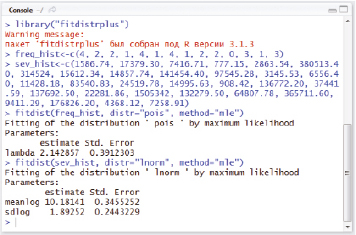
Рис. 1. Оценка максимального правдоподобия в среде RStudio
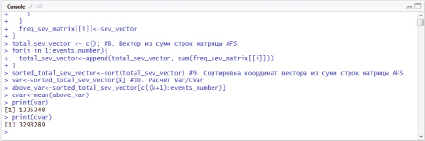 Рис. 2. Выполнение скрипта для расчёта OpVar и OpCVar
Рис. 2. Выполнение скрипта для расчёта OpVar и OpCVar
На рис. 2 изображены результаты выполнения программного кода в среде RStudio.
Исходя из рис. 2 потери для внедряемого релиза 15 могут быть выражены в следующих показателях:
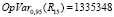 руб.
руб.
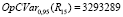 руб.
руб.
Изобразим графически упорядоченные значения потерь 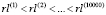 , а также величину OpVar (рис. 3). Для этого необходимо выполнить следующий скрипт:
, а также величину OpVar (рис. 3). Для этого необходимо выполнить следующий скрипт:
plot(sorted_total_sev_vector, axes = FALSE, type=»l», ylim=c(0,2000000), xlab=»номер сценария», ylab=»величина ущерба (руб.)»,) # 1. Построение основного графика
axis(1, pos=0) # 2. Построение оси OX
axis(2, pos=0, las=1) # 3. Построение оси OY
points(k,0, pch=19) # 4. Отметим на графике OpVar
text(k, 0, k, pos=3)
points(k, var, pch=19)
text(k, var, «OpVar», pos=2)
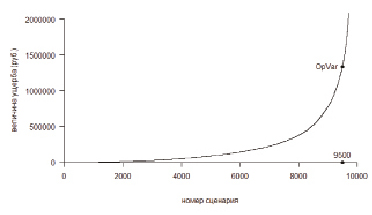
Рис. 3. Упорядоченные значения потерь по 10000 сценариям
В рамках рассмотренного нами примера предположим, что в течение 10 последующих релизов (релизы 15–24) внедрялись новые методы тестирования и, как следствие, была уменьшена частота инцидентов:
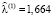 .
.
Рассчитаем OpVar для релиза 25:
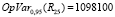 руб.
руб.
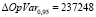 руб.
руб.
Отсюда можно сделать вывод, что новые методы тестирования привели к сокращению максимального ожидаемого ущерба на 237 248 руб.
Заключение
В работе сделан вывод о том, что для критичных банковских систем установка каждого нового релиза в промышленную среду может привести к возникновению инцидентов операционного риска и, как следствие, к существенным финансовым потерям. Этим объясняется необходимость интеграции процесса управления релизами и процесса управления рисками при разработке банковского ПО.
В статье описаны способы минимизации IT-рисков на всех этапах жизненного цикла IT-релизов; разработана математическая модель оценки рисков, основанная на методе Value at Risk. Предложенная автором модель сопровождается практическим примером, а также программным кодом R.



