Задачи имитации эргатических систем заключаются в воспроизведении штатных условий эксплуатации, предпосылок возникновения особых ситуаций и их протекания, как при правильных, так и неправильных действиях оператора во всем принятом для имитации диапазоне ожидаемых условий эксплуатации. Резкое усложнение объектов и их систем повлекло за собой и усложнение имитаторов, что привело к увеличению как стоимости опытно-конструкторских разработок, так и времени, затрачиваемого на поиски приемлемого конструкторского решения.
Так, одним из наиболее сложных и важных этапов создания авиационных тренажеров является разработка имитатора динамики полета. Совершенствование моделей динамики полета происходит на основе построения рациональных математических моделей на базе гибкого модульного программно-математического обеспечения, автоматизации проектирования и испытаний, новых методик идентификации и корректировки математических моделей. В числе особо важных задач:
– разработка и внедрение единой автоматизированной системы сбора и обработки информации для моделирования динамики полета;
– формирование банка исходных данных, создание технологии его формирования и корректировки;
– разработка рациональных математических моделей на базе унифицированного модульно-блочного программно-математического обеспечения по классам летательных аппаратов;
– определение требуемой точности моделирования летно-технических характеристик, исходя из обучающих свойств тренажеров с разработкой характеристик и обоснованных допусков на каждую из них.
– разработка методики идентификации и корректировки летно-технических характеристик тренажера под реальный объект управления с разработкой критериев по всем режимам полёта;
– разработка и внедрение системы автоматизированного проектирования и испытаний имитатора динамики полета.
Единая автоматизированная система сбора, обработки и корректировки исходной информации должна предусматривать:
– использование эффективной технологии сбора исходной информации;
– использование исходной информации, включающей аэродинамические коэффициенты, геометрические данные, моменты инерции, летно-технические характеристики и другие данные, необходимые для создания математической модели динамики полета различных классов объекта;
– использование эффективных методов, обеспечивающих приемлемые сроки корректировки банка исходных данных;
– использование математического описания аэродинамических коэффициентов с указанием системы координат и др.
В настоящее время математическая модель динамики полета строится по принципу гибкой модульной структуры с оптимизацией взаимосвязей, обеспечивающей максимально возможную унификацию. Модули должны иметь законченное программно-математическое обеспечение. Структура модели должна обеспечивать возможность корректировки выходных характеристик тренажера под реальные летно-технические характеристики объекта управления. Предполагается наличие модуля для автоматизированной проверки исправной работы модели. По каждому модулю должно быть определено допустимое время вычислений. Обоснование требуемой точности моделирования динамики полета должно выполняться исходя из условий формирования полноценных профессиональных навыков при обучении на тренажере. Объективные показатели имитационных свойств тренажеров должны позволить провести оценку: результирующих характеристик пилотирования, качества управления, основных эргономических характеристик. Предусматривается сравнение групп показателей для условий имитатора и реального объекта.
Отметим, что методика идентификации должна быть увязана с перечнем летно-технических характеристик. Предполагается возможность корректировки модулей динамики полета.
Рассматриваемая задача непосредственно связана с разработкой методов оценки качества управления в эргатической системе. Предпочтение отдается методам, которые в дальнейшем могут использоваться при решении задачи идентификации целостной человеко-машинной системы в виде целостной же системы «оператор – имитационная модель объекта». Укажем основные теоретические трудности решения задачи идентификации эргатических систем. Несмотря на обилие литературы по этому вопросу, авторы избегают принципиальных трудностей. Так, в научных школах «человек-оператор» рассматривается как некоторое собирательное понятие: «система отображения информации + человек + органы управления». Описывается связь входного сигнала, поступающего на оператор, с выходным сигналом, на основе сравнения текущего входного сигнала с опорным. Однако фактически умалчивается, что опорный сигнал практически не формализуется. Поэтому впоследствии была предложена (по каждому из каналов управления) сравнительно простая структурная схема (рис. 1) эргатической системы [1]. Из схемы с очевидностью следует, почему в литературе уходят от формализованного рассмотрения структурной схемы: все дело в том, что не формализуется элементарнейший сумматор, без чего нельзя составить уравнение замыкания.
Поэтому можно лишь косвенными методами решить задачу идентификации эргатической системы. Отсутствие уравнения замыкания (невозможность его получения) не позволяет во входном сигнале (в управляющих движениях оператора), поступающем на объект, выделить сигнал, коррелированный с выходным сигналом. Теоретически задачу идентификации никогда не решить, так же как только экспериментально. Однако требуется ясность в понимании именно теоретических трудностей. Поэтому предлагается теоретико-экспериментальный метод идентификации целостной эргатической системы. Существует тенденция свести задачу имитационного моделирования эргатической системы к идентификации лишь объекта моделирования. В предлагаемом методе предусматривается ретроспективное определение по данным нормальной эксплуатации обобщенных характеристик двух систем: «оператор – объект управления» и «оператор – имитационная модель»; находятся параметры имитационной модели: сначала по данным, полученным только для объекта, затем (экспериментально) для системы «оператор – имитационная модель». Итерационно определяется передаточная функция некоторого корректирующего устройства, учитывающего влияние коррелированного с выходным сигналом части входного сигнала (эксперимент, доводка имитационной модели, определение передаточной функции корректирующего устройства; эксперимент, доводка имитационной модели и т.д.).
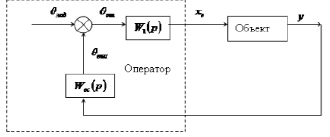
Рис. 1. Структурная схема управления продольным движением: Wос(р) – передаточная функция анализатора, W1(р) – передаточная функция моторной части оператора, сумматор – сравнивающее «устройство» центральной нервной системы
Как уже отмечалось, в силу трудностей описания человека многие авторы ограничиваются идентификацией лишь собственно объекта. Но при идентификации должны быть получены все частные операторы не только объекта, но и человека. Характеристики имитационной модели должны быть такими, чтобы управляющие воздействия в системах «оператор – имитационная модель» и «оператор – объект» были по возможности близкими (передаточные функции оператора совпадают). В число передаточных функций оператора входят операторы формирования управляющих воздействий по различным каналам управления (визуальный, шумовой, акселерационный, тактильный и т.д.); при имитационном моделировании требуется создание информационного подобия двух указанных эргатических систем. Известно, в соответствии с организмическим принципом (человек в эргатической системе ведет себя организмически оптимально) объект предопределяет поведение оператора. Это несколько облегчает задачу: появляется возможность свести оценку точности идентификации к оценке структуры не вообще всего класса управляющих движений оператора, а лишь оптимальных управляющих воздействий в системах «оператор – имитационная модель» и «оператор – объект», когда процесс адаптации оператора уже завершился. До настоящего времени в практике обучения полная адаптация вообще не допускается, чтобы избежать формирования ложных навыков. Из этого с очевидностью следует, схожесть управляющих движений на реальном объекте и модели, а стало быть, и близость оптимальных управлений может быть достигнута лишь тогда, когда с достаточной для практических целей точностью (оценка по схожести управлений) будет проведена идентификация эргатической системы «оператор – объект». Пришли к важному выводу: определение качества управления в эргатической системе является лишь первым шагом при идентификации, возможным и крайне необходимым ее инструментом.
Ясно, оценка качества управления или попросту структуры управляющих движений является многокритериальной. Однако оценка по векторному критерию во многих случаях практически невозможна, поскольку критерии, как правило, противоречивы. Нередко осуществляется скаляризация системы частных критериев (свертывание критериев в один – глобальный интегральный критерий). Какие же частные критерии стоит вводить в глобальный критерий, характеризующий стиль управления, и как определить весовые коэффициенты частных критериев, входящих в глобальный критерий? Так как частные критерии являются разно-размерными, возникает задача их нормализации. Как установить, действительно ли эти критерии существенны или нет? Как, наконец, по глобальному критерию определить балльную оценку структуры управляющих движений?
Такой теоретико-экспериментальный подход был реализован при разработке различных комплексов для подготовки операторов транспортных систем [2–4]. Использовался единый алгоритм объективной оценки качества управления, основанный на использовании спектральных характеристик центрированных процессов управления. Определение кодированных значений частных критериев производилось с учетом интервалов их изменения в ансамбле реализаций. Весовые константы находились с учетом корреляционных связей между частными, групповыми и глобальным критериями (устанавливался физический смысл каждого из них). Предусматривалась оценка как в десятибалльной, так и в другой любой шкале. В оценке участвовали только те процессы, которые укладывались в заданном коридоре (положительные оценки).
Естественным является желание использовать разработанные методы оценки качества управления при идентификации. Поэтому одновременно с методикой оценки управляющих движений, основанной на использовании обычных спектров Фурье, анализировалась возможность использования обобщенных рядов Фурье, в частности разложение управляющих воздействий по ортогональным полиномам Ляггера. Они позволили не только идентифицировать управляющее движение, но и определить обобщенные передаточные функции эргатических систем (при известных спектрах управляющих движений и выходных величин). В ряде случаев использовались ортогональные полиномы Чебышева.
Трудности идентификации усугублялись некорректностью задачи определения передаточных функций в частотной области по спектральным характеристикам. Здесь некорректность понимается в смысле малой устойчивости результатов (в зависимости от вида входных процессов ошибка может быть сколь угодно велика). Поэтому возникает необходимость выделения ортонормированной системы, по которой следует разлагать процессы. Напрашиваются аналогии: связь разработанной оптимальной системы и функционала качества; связь передаточных свойств и спектральных характеристик [4–6].
При разработке обучающих комплексов параллельно использовались:
– экспериментальная оценка точности определения спектральных характеристик, связь спектральных характеристик с параметрами управляющих движений как импульсных процессов;
– определение интервалов достоверности результатов в частотной области, в том числе на основе μ-критерия;
– выбор ортонормированной системы с быстрой сходимостью обобщенного ряда Фурье при идентификации (такой системой оказалась система полиномов Ляггера).
При анализе случайных сигналов на входе объекта использовались статистические характеристики источников этих сигналов. В качестве меры неопределенности значения некоторого параметра ai принималось среднеквадратичное значение дисперсии. А именно:
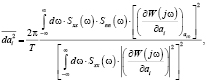
ai – i-й параметр в передаточной функции модели W(jω);
ai0 – значения параметров W(jω), при которых модель и объект оказываются идентичными (фактически определенные значения параметров ai);
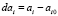– отклонения параметров;
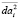– среднеквадратичное значение дисперсии параметра;
Sxx – спектральная плотность x(t);
Snn – спектральная плотность n(t).
Указанные недостатки методов идентификации в частотной области привели к необходимости оценки и иных методов идентификации, в частности регрессионной идентификации. Она позволяет определить параметры уравнений движения системы «оператор – объект» для реализации этих параметров в системе «оператор – имитационная модель» [7].
При обработке экспериментальных данных использовалась серия алгоритмов для статистического анализа. Это касается определения параметров дискретизации, интервалов усреднения, выбор длительности реализации, алгоритмов определения вероятностей частот в управляющих движениях по спектральным характеристикам и др.
Рядом исследователей указывается необходимость достижения полного информационного подобия в системах «оператор – объект» и «оператор – имитационная модель». Однако возможен и другой подход – деформация динамических свойств объекта в имитационной модели для компенсации информационного дефицита (отсутствие информационного подобия). В частности, можно воспользоваться методом целенаправленной деформации динамических характеристик объекта на основе расширенного использования методов математического планирования эксперимента (позволит уменьшить риск, связанный с использованием метода проб и ошибок) [8, 9].
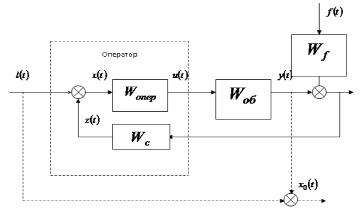
Рис. 2. Структурная схема системы «оператор – имитационная модель»
При оценке требований к реализации динамических характеристик объекта в имитационной модели структурная схема системы «оператор – имитационная модель» представлялась в виде, приведенном на рис. 2.
Стиль управления в эргатической системе определяется внутренней структурой сигнала ошибки
; 
;
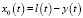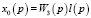в режиме стабилизации l(t) можно рассматривать как стационарную случайную функцию.
Здесь
,
, 
;
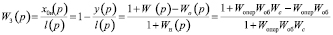
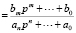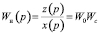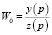Wн(р) – передаточная функция разомкнутой системы, W0 – передаточная функция прямого разомкнутого канала, W1 – передаточная функция обратной связи.
Синтез имитационной модели объекта сводился к определению параметров Wоб так, чтобы в системе «оператор – имитационная модель»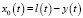 
имела требуемую внутреннюю структуру (определяется видом 
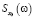), во всяком случае, заданные 
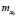и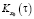 
, или заданную спектральную характеристику 
.
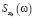Справедливо
,
,
.
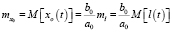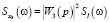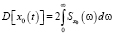Таким образом, если известна функция l(t), то для получения требуемой структуры x0(t) следует определить параметры W3(р) по известным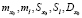 
.