В настоящее время повсеместно используются асимметричные схемы цифровой подписи. В Российской Федерации действующим стандартом такой цифровой подписи является ГОСТ Р 34.10-2012 [1].
Как показали предыдущие исследования [2], ассиметричные схемы являются достаточно криптостойкими, однако, нет гарантий, что в будущем такие ЭЦП не будут взломаны, так как нет теоретического доказательства того, что задачи дискретного логарифмирования в группе точек эллиптической кривой, на которых они базируются, не могут быть решены.
Таким образом, перспективным направлением представляется работа над созданием и исследованием симметричных схем цифровой подписи, использующих «классические» блочные шифры в своей основе.
Первыми на возможность создания симметричной схемы ЭЦП указали исследователи Диффи и Хеллман [3], однако в то время, когда они занимались этим вопросом, не было достаточно стойких классических алгоритмов шифрования, поэтому их идея не получила большого распространения. Сегодня же существует достаточное количество блочных шифров, обладающих высокой криптостойкостью [4–6]. В частности, в июне 2015 г. в РФ утвержден новый стандарт в области криптозащиты ГОСТ Р 34.12-2015, который описывает шифр «Кузнечик», представляющий собой sp-сеть [7, 8].
Согласно ГОСТ Р 34.12-2015 128-битный блок информации на входе шифруется следующим образом:
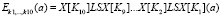. (1)
Для дешифрования используются те же преобразования, которые применяют в обратном порядке:
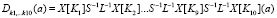. (2)
Схема цифровой подписи Диффи и Хеллмана в своей основе содержит три алгоритма:
1. Алгоритм G выработки ключевой пары:
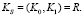(3)
2. Алгоритм S выработки цифровой подписи для бита t (t∈0, 1}):
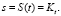(4)
3. Алгоритм V проверки подписи для нашего t:
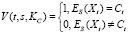. (5)
где KC – ключ для проверки, который вычисляется по формуле (6) в виде результата двух процедур шифрования по алгоритму Ek:
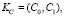(6)
где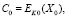 
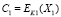, блоки X0 и X1 известны всем участникам обмена информацией.
Помимо отсутствия надежного шифра распространению схемы Диффи и Хеллмана помешал ряд существенных недостатков, которыми эта схема обладала, среди которых можно выделить то, что алгоритм ЭЦП поддерживает возможность подписи только одного бита, а также в процессе подписи рассекречивается половина ключа.
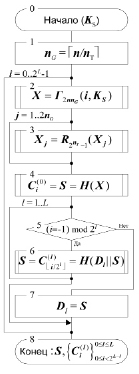
Рис. 1. Алгоритм получения ключа проверки ЭЦП
Рис. 2. Алгоритм подписи хэш-кода массива данных
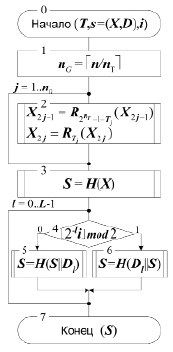
Рис. 3. Алгоритм проверки подписи хэш-блока
Для преодоления этих недостатков предлагается использовать модификацию битовых групп, предложенную Б.В. Березиным и П.В. Дорошкевичем [9].
Модифицирование заключается в подписи целых наборов бит и осуществляется следующим образом: пусть n ≤ nk и расширение n в nK-битовые блоки осуществляется процедурой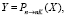 
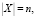
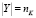, тогда функция «односторонней криптографической прокрутки» блока T размером n бит k раз определяется рекурсивной функцией
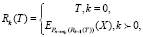(7)
где X – случайный n-битовый блок информации.
Функция осуществляет k раз процедуры:
1) расширение n блока T до размерности nk,
2) на полученном T зашифровать блок информации X,
3) результат второго пункта внести T.
Ниже приведены алгоритмы симметричной схемы цифровой подписи, использующей в качестве алгоритма шифрования блочный шифр «Кузнечик».
Ключ формируется с помощью генератора псевдослучайных кодов.
Схемы алгоритмов цифровой подписи представлены на рис. 1–3.
Данная схема была реализована программным путем на языке высокого уровня С++ (рис. 4).
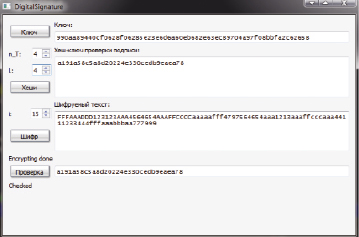
Рис. 4. Программная реализация, где: n_T – длина подблока; L – фактор подписи; i – входной параметр
Для реализации использовались библиотеки libgcc_s_dw2-1.dll, libstdc++-6.dll, libwinpthread-1.dll, Qt5Cored.dll, Qt5Guid.dll, Qt5Widgetsd.dll. В рамках программы использованы расширения стандартных unit64_t до 128 и 256 бит. Сборка программы осуществлялась с библиотеками Qt 5.7.0 под компилятор «MinGW». Для генерации ключа использовался криптостойкий генератор, интегрированный в программу.
Так, например, при параметрах n_T = 2, L = 1, I = 1 время проверки подписи на тестовом стенде (таблица) занимает 1018 миллисекунд.
Характеристики тестового стенда
|
Материнская плата |
Supermicro, X9DR3-F, Версия BIOS American Megatrends Inc. 1.1, 03.10.2012 |
|
Процессор |
AMD A10-5750M APU with Radeon(tm) HD Graphics 2.50 GHz |
|
ОЗУ |
8 Гб |
|
Жесткий диск |
256 Gb SSD |
|
ОС |
Windows 8 |
Таким образом, данная схема имеет следующие достоинства:
1. Механизмы выработки, получения и проверки ключей и подписи работоспособны и достаточно просты.
2. Для подписи бита t необходимо по отношению к s решить ES(Xt) = Ct, т.е. это невозможно, если неизвестен ключ.
3. Так как алгоритм криптостойкий и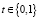 
, поэтому подобрать подходящий к подписи t не представляется возможным.
4. Только стойкость шифра оказывает влияние на ЭЦП.
Работа выполнена при поддержке гранта Минобрнауки № 2.6264.2017/8.9.