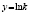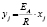Настоящая статья посвящена компьютерной обработке экспериментов по кинетике химических реакций. В нашем институте кинетика химических реакций изучается в процессе разработки технологических процессов комплексной фторидной переработки для различных видов алюмосиликатного сырья Верхнего Приамурья [1]. Результатами экспериментального исследования по кинетике химической реакции являются значения концентраций некоторого вещества Сik(tik) в заданные моменты времени tik (i = 1, …, nk, где nk – количество отсчетов времени при температуре Tk, k = 1,2, …, l, где l – количество температур). Количество рабочих температур l, допустимое в программе, от двух до четырех. Количество отсчетов времени nk, в общем случае, для разных температур Tk отличается и изменяется от 3 до 9.
Результатами обработки экспериментальных данных являются константы скоростей и энергии активации, а также зоны протекания и механизмы реакции. Знание зоны и механизма реакции при той или иной температуре дает знание о физико-химическом процессе, который обуславливает её протекание и позволяет управлять ходом реакции. Сравнение констант скоростей и энергий активаций различных реакций позволяет сопоставлять между собой эти реакции.
Вычисления констант скоростей в работе мы проводим, используя четыре вида физико-химических процессов, соответствующих четырем законам изменения концентраций: степенному (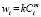 ), Авраами (
), Авраами (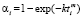 ), экспоненциальному (
), экспоненциальному (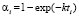 ) и Праута – Томпкинса
) и Праута – Томпкинса 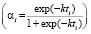 , где wi – скорость реакции, Ci – концентрация вещества, αi – степень превращения вещества, k – константа скорости. Степенной закон описывает столкновения частиц, остальные три – различные виды диффузии. В соответствии с этим зона реакций, описывающихся степенным процессом кинетическая, для остальных трех процессов – диффузионная [2].
, где wi – скорость реакции, Ci – концентрация вещества, αi – степень превращения вещества, k – константа скорости. Степенной закон описывает столкновения частиц, остальные три – различные виды диффузии. В соответствии с этим зона реакций, описывающихся степенным процессом кинетическая, для остальных трех процессов – диффузионная [2].
Для определения механизма реакции в программе используются значения погрешностей аппроксимаций. Считаем, что механизм реакции при данной температуре определяется тем законом изменения концентраций, при котором погрешность аппроксимации при данной температуре минимальна. Поскольку погрешности аппроксимаций вычисляются для каждой температуры, постольку механизм реакций для каждой температуры может быть своим. В программе организован автоматический отбор данных (констант скоростей, энергий активации, зон и механизмов реакций) для каждой из исследуемых температур [3].
Цель исследования
Отправной точкой исследования в данной работе являются данные по кинетике химических реакций. Цель исследования – определить кинетические характеристики реакции. Математическая обработка результатов экспериментов значительно облегчается при использовании компьютерной расчетной программы. С целью разработки компьютерной программы создавался алгоритм расчета с последующей программной реализацией, первоначально средствами приложения Microsoft Access 2007 c применением vba. В данной работе описывается программа для обработки экспериментальных данных по кинетике с расчетом кинетических параметров: констант скоростей, энергий активаций, зон и механизмов реакций, написанная на языке Visual Basic Community 2015.
Материалы и методы исследования
Методами исследования в работе являются регрессионный анализ [4] и компьютерный расчет. Для каждого из упомянутых выше процессов методом линеаризации его уравнения строится уравнение регрессии. Линеаризация осуществляется в случае степенного, экспоненциального законов и уравнения Праута – Томпкинса логарифмированием, а в случае Авраами – методом двойного логарифмирования. Полученные в результате уравнения регрессии являются нелинейными. Путем замен переменных мы осуществляем переход к двум линейным моделям регрессии: с угловым коэффициентом и свободным членом в случае степенного закона и Авраами и с одним угловым коэффициентом в случае экспоненциального закона и уравнения Праута – Томпкинса (см. табл. 1). Далее, по формулам метода наименьших квадратов вычисляем значения угловых коэффициентов и свободных членов. В случае степенного закона и уравнения Авраами угловой коэффициент равен порядку реакции, а свободный член равен логарифмам константы скорости. В случае экспоненциального закона и уравнения Праута – Томпкинса угловые коэффициенты представляют собой константы скоростей.
Таблица 1
Модели нелинейных регрессий, замены переменных для перехода к линейным моделям и их уравнения для используемых в программе процессов
|
Наименование закона |
Математическая формулировка закона |
Нелинейная регрессия |
Замена переменных |
Линейная регрессия |
|
Линейный |
|
|
|
|
|
Степенной |
|
|
|
|
|
Авраами |
|
|
|
|
|
Экспоненци-альный |
|
|
|
|
|
Праута – Томпкинса |
|
|
|
|
|
Аррениуса |
|
|
|
|
Энергии активаций в программе рассчитываются по уравнению Аррениуса для констант скоростей [5]. После преобразования, логарифмирования и замены переменных получается уравнение с одним угловым коэффициентом, который рассчитывается методом наименьших квадратов. Угловой коэффициент равен энергии активации, деленной на универсальную газовую постоянную R (последняя строка в табл. 1).
В программе рассчитываются погрешности аппроксимаций по формуле
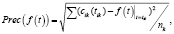 (*)
(*)
где cik(tik) – экспериментальные значения концентраций в моменты времени tik, 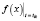 – расчетное значение, полученное по исследуемому закону в точках tik при температуре Tk, а nk, как и ранее, количество отсчетов времени при данной температуре.
– расчетное значение, полученное по исследуемому закону в точках tik при температуре Tk, а nk, как и ранее, количество отсчетов времени при данной температуре.
Отбор зависимости с меньшей погрешностью аппроксимации, а следовательно, и определяющего механизма реакции при данной температуре осуществляется в программе автоматически.
Кроме того, в работе проводится проверка статистических гипотез об адекватности каждой из моделей регрессий по критерию Снедекора – Фишера, а также о значимости коэффициентов этих моделей регрессии по t-критерию Стьюдента [4]. Проверка гипотезы об однородности дисперсий воспроизводимости в работе не проводится, поскольку в каждой точке факторного пространства осуществляется только одно измерение.
Результаты исследования и их обсуждение
Программа Кинетика для расчета кинетических характеристик гетерофазных реакций написана на языке Visual Basic [6] в интегрированной среде разработки программного обеспечения Visual Studio Community 2015.
Программа имеет десять вкладок: Вход, Кинетика, Зона реакции, Графики, СтатистикаХ (Х = 0, …, 5).
Вкладка Вход предназначена для размещения элементов управления, осуществляющих ввод данных: массивы концентраций КонцX(i) и времен ВремяХ(i), строку температур TемперХ (X = 1,…,4; i = 1, 2, …, n), число точек отсчетов времени nk, количество рядов данных l, максимальные времена и концентрации для каждой из температур Tk.
Уровень значимости (устанавливается выбором одного из восьми значений в списке в ComboBox-поле [7]) служит для выбора коэффициентов Стьюдента и Снедекора – Фишера из таблиц Excel Стьюдент и Фишер, подключенных к программе.
После выбора уровня значимости нажатием кнопки Вычислить на вкладке Вход запускается процедура вычисления всех предусмотренных характеристик. Первым делом создаются двумерные массивы концентраций и времени Time(i, j) и Сonc(i, j), одномерные массивы температур Temperature(k) и обратных температур ReTemp(k) = 1/(Temperature(k) + 273), k = 1,…, l.
Далее осуществляется переход к относительным величинам концентрации и времени Time_norm(i, j) и Сonc_norm(i, j), делением на максимальные значения. Затем вводятся обобщенные координаты, представляющие трехмерные массивы abscissa(4, 9, 4) и ordinate(4, 9, 4), в которых первый индекс означает порядковый номер закона изменения концентраций от 0 до 4, второй – порядковый номер отсчета времени от 3 до 9, третий – порядковый номер температурного ряда от 1 до 4. Приведем фрагмент программы, в котором осуществляется ввод обобщенных переменных:
If j = 0 Then ordinate (j, i, k) = Conc_norm (i, k): abscissa (j, i, k) = Time_norm (i, k)
If j = 1 Then ordinate (j, i, k) = Math.Log (Rate (i, k)): abscissa (j, i, k) = Math.Log (Conc_norm(i, k))
If j = 2 Then ordinate (j, i, k) = Math.Log (-Math.Log (1 – Conc_norm (i, k))): abscissa(j, i, k) = Math.Log(Time_norm(i, k))
If j = 3 Then ordinate (j, i, k) = Math.Log (1 – Conc_norm (i, k)): abscissa (j, i, k) = Time_norm (i, k)
If j = 4 Then ordinate (j, i, k) = Math.Log (Conc_norm (i, k) / (1 – Conc_norm (i, k))): abscissa (j, i, k) = Time_norm (i, k).
После этого происходит вычисление сумм для метода наименьших квадратов:
Sx (j, k) = Sx (j, k) + abscissa (j, i, k)
Sy (j, k) = Sy (j, k) + ordinate (j, i, k)
Sxy (j, k) = Sxy (j, k) + abscissa (j, i, k) * ordinate (j, i, k)
Sx2 (j, k) = Sx2 (j, k) + Math.Pow (abscissa (j, i, k), 2),
где Sx (j, k), Sy (j, k), Sxy (j, k) и Sx2 (j, k) – суммы абсцисс, ординат, произведений абсцисс на ординаты и квадратов абсцисс соответственно.
Далее в программе рассчитываются свободные члены и угловые коэффициенты регрессий для каждой модели регрессии (каждого из законов изменения концентрации) и при каждой температуре. Константы скоростей ConRat(j,k) для линейной модели (j = 0) равны свободному члену, для степенного закона (j = 1) и уравнения Авраами (j = 2) вычисляются взятием экспоненты от свободного члена, а порядки реакций m(j,k) для этих двух законов равны угловым коэффициентам (строки вторая и третья сверху табл. 1). Константы скоростей для экспоненциального закона (j = 3) и уравнения Праута – Томпкинса (j = 4) равны угловым коэффициентам соответствующих уравнений регрессий (в табл. 1 сверху строки 4 и 5).
Погрешности расчета констант скоростей pK(j,k) и порядков реакции pM(j,k) вычисляются по формулам для расчета коэффициентов регрессии [8], а погрешность аппроксимации Prec(j, k) рассчитывается по формуле (*). Погрешности расчета констант скоростей pK(j,k) и аппроксимаций Prec(j, k) вычисляются для каждой модели и при каждой температуре. Погрешности порядков реакций pM(j,k) вычисляются для моделей с j = 1, 2.
Вычисление энергий активаций производится по формуле, приведенной в последнем столбце шестой сверху строки табл. 1. В данной модели регрессии переменными являются обратные температуры ReTemp(k) и логарифм константы скорости ConRat(j, k). Из этой формулы следует, что энергия активации равна угловому коэффициенту данной модели, умноженному на универсальную газовую постоянную. Для каждой модели вычисляется одно значение энергии активации. Вычисляется также для каждой модели и погрешность энергии активации pE(j).
Расчет констант скоростей, погрешностей констант скоростей, погрешностей аппроксимаций, а также порядков реакции и их погрешностей приводится на вкладке Кинетика.
На вкладке Зона реакции (см. рис. 1) располагаются результаты автоматизированного отбора: данные о тех зонах и механизмах реакции, которые (по результатам расчета и отбора) имели место при каждой температуре. Сюда входят также значения констант скоростей, погрешностей их вычислений и погрешностей аппроксимаций, и энергий активаций.
Нажатием кнопки Вывод на вкладке Зона реакции происходит вывод данных в таблицу Microsoft Word. Вывод данных осуществляется при помощи отдельной процедуры, которая осуществляет автоматическое форматирование текста и таблицы. В программе предусмотрены вывод и заполнение таблицы для различного количества рядов данных (от двух до четырех).
На рис. 1 в качестве примера показаны результаты расчета реакции фторирования анортозитов гидродифторидом аммония. Из этого рисунка видно, что данная твердофазная реакция при всех температурах протекает в диффузионной зоне, при нижней и средних температурах по уравнению Авраами, а при верхней температуре по экспоненциальному закону. Энергия активации для Авраами равна в данном случае 19,1 кДж/моль, а для экспоненциального закона равна 19,7 кДж/моль. Несмотря на различные механизмы реакции, энергии активации близки и константы скорости монотонно возрастают от 0,004483 мин-1 до 0,017836 мин-1. По-видимому, это связано с тем, что порядки реакции для Авраами оказались близки к 1 и приняли значения 0,86; 0,91; 0,96; 1,09 (см. рис. 2). Из сравнения уравнения Авраами с экспоненциальным законом очевидно, что при порядке, равном 1, уравнение Авраами переходит в экспоненциальный закон.
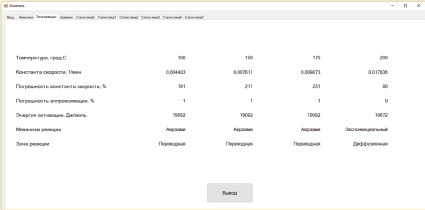
Рис. 1. Вкладка Кинетика программы Кинетика с результатами расчета на примере реакции фторирования анортозитов гидродифторидом аммония
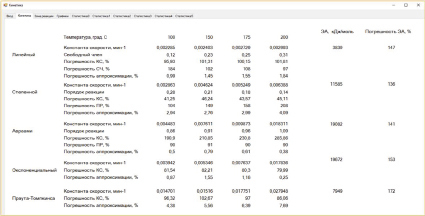
Рис. 2. Вкладка Кинетика программы Кинетика с результатами расчета на примере реакции фторирования анортозитов гидродифторидом аммония
Таблица 2
Статистическая проверка гипотез об адекватности моделей регрессии и о значимости коэффициентов регрессий по Снедекору – Фишеру и Стьюденту соответственно
|
Закон |
Авраами |
Экспоненциальный |
||||||
|
Температура, °С |
100 |
150 |
175 |
200 |
100 |
150 |
175 |
200 |
|
Коэффициент Стьюдента |
2,01 |
2,01 |
2,01 |
2,01 |
1,94 |
1,94 |
1,94 |
1,94 |
|
Статистика для свободного члена |
0,27 |
0,97 |
1,25 |
1,81 |
0,62 |
1,11 |
0,68 |
0,1 |
|
Статистика для углового коэффициента |
2,22 |
2,21 |
2,22 |
2,23 |
2,38 |
2,36 |
2,42 |
2,43 |
|
Коэффициент Фишера |
6,26 |
6,26 |
6,26 |
6,26 |
4,95 |
4,95 |
4,95 |
4,95 |
|
Статистика Фишера |
1,72 |
1,25 |
1,09 |
1,17 |
4,73 |
2,67 |
2,12 |
1,52 |
В программе осуществляется статистическая проверка гипотез об адекватности регрессионной модели с использованием критерия Снедекора – Фишера и о значимости коэффициентов регрессии по t-критерию Стьюдента (см. табл. 2).
Статистическая проверка показала адекватность моделей с j = 2, 3, 4 при всех температурах. Модели с j = 0 и 1 неадекватны при нижней температуре. Проверка значимости коэффициентов регрессии показала значимость угловых коэффициентов регрессий для моделей с j = 0, 2, 3, 4 при всех температурах, с j = 1 при нижней температуре. Свободные члены значимы только для степенного закона при верхней температуре.
Вернемся к рис. 1. Отобранные по минимуму погрешностей аппроксимаций механизмы, Авраами и экспоненциальный, подвергнем статистическому анализу. Заметим, что константы скоростей для Авраами вычисляются взятием экспоненты от свободного члена, который согласно t-критерию Стьюдента является статистически незначимым при всех температурах. По-видимому, нам следует считать, что механизмом реакции является экспоненциальный закон, в том числе при нижних и средних температурах. Энергия активации, следовательно, будет равна 19,7 кДж/моль при всех температурах, а константы скоростей будут иметь значения 0,003942; 0,005346; 0,007637; 0,017836 (см. рис. 2).
Программа Кинетика для расчета кинетических характеристик опробовалась на расчетах различных реакций в процессе комплексной фторидной переработки алюмосиликатного и силикатного сырья с извлечением полезных продуктов [1, 3].




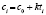
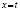 ;
; 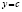 ;
; 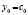
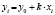
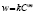
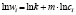
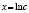 ;
; 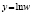 ;
;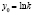
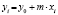
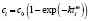
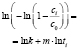
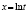 ;
; 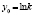 ;
;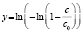
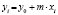
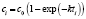
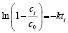
 ;
;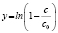
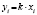
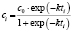
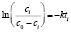
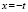 ;
;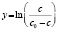
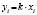
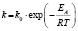
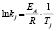
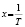 ;
;