Формирование расписания занятий является одной из основных и наиболее сложных задач автоматизации управления учебным процессом вуза. В связи с большими различиями организации высшего образования в разных странах сделана попытка стандартизации ограничений для задач расписаний [9]. При учете всех ограничений, включая NP-полноту задачи, на передний план выходят эвристические методы, такие как имитация отжига [7], поиск с запретами [5, 8], эволюционные алгоритмы [10, 11]. В основе эвристик мультипроектного планирования находятся схемы формирования расписаний (SGS – schedule generation scheme) и правила приоритетов (PR – priority rules) [6]. Приоритетами являются критерии для определения очередности конкурирующих по ресурсам работ/проектов. В исследованиях по формированию расписаний вузов подобных подходов не обнаружено. Для решения задачи формирования расписания занятий вуза предложены эвристики, основанные на критериях загруженности и равномерности использования ресурсов [1, 3].
Целью данной статьи является представление схем генерации и правил приоритетов на основе методов ранжирования в программном формировании расписания занятий российского высшего учебного заведения. Все занятия полагаются независимыми друг от друга.
Задача формирования расписания занятий вуза является задачей распределения трех ресурсов – студенческого контингента, преподавателей и аудиторий при проведении трех видов занятий: занятие одной группы с одним преподавателем; занятие нескольких групп с одним преподавателем – занятие потока; занятие одной группы с несколькими преподавателями – занятия подгрупп группы.
Расписание занятий составляется, прежде всего, для студентов, наиболее удобным для которых является расписание, занятия в котором проводятся в разные дни недели в одно и то же время. То есть качество расписания должно определяться такими факторами, как идентичность учебных дней каждой группы по количеству и времени проведения занятий, равное количество проводимых в один день занятий и т.п. Эти факторы применяются как оценки равномерности занятий в расписаниях групп [1].
Исходными данными для формирования расписания занятий являются заявки групп, в которых указывается студенческий контингент, преподаватель, дисциплина, вид занятия и требуемые или желаемые аудитории с набором признаков. Основной признак аудитории – вместимость. Дополнительными признаками могут быть требуемое оборудование – лабораторное, компьютерное, мультимедийное и т.п. Аудитория в заявке группы может иметь «пустое» значение – Null, заменяемое конкретным значением при формировании расписания. Студенческий контингент в заявке группы представлен группой, потоком и подгруппой. В зависимости от вида занятия поток и подгруппа могут иметь значения Null. Заявки групп формируются для каждой «пары» занятий каждой группы для двух недель расписания. На основе заявок групп перед началом формирования расписания формируются заявки занятий, далее заявки, структура которых в зависимости от типа занятия имеет различный характер.
Для формирования расписания занятий высшего учебного заведения использованы две последовательно применяемые схемы генерации расписаний [2]:
- конструктивная эвристика SGS1 – стратегия формирования начального расписания;
- оптимизационная эвристика SGS2 – стратегия оптимизация расписания.
Введем необходимые в математическом моделировании расписания обозначения.
Исходные данные задачи:
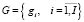 – множество академических групп;
– множество академических групп;
P, R – множества потоков и подгрупп академических групп;
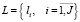 – множество преподавателей;
– множество преподавателей;
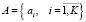 – множество аудиторий;
– множество аудиторий;
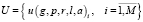 – множество заявок групп, где:
– множество заявок групп, где:
– p – конкретный поток или – NULL;
– r – конкретная подгруппа или – NULL;
– l – конкретный преподаватель или – NULL;
– a – конкретная аудитория или NULL.
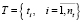 – множество таймслотов – временных интервалов проведения занятий, однозначно определяющих номер «пары» – tn, день недели – td и ее признак – ts;
– множество таймслотов – временных интервалов проведения занятий, однозначно определяющих номер «пары» – tn, день недели – td и ее признак – ts;
nt – общее число таймслотов интервала расписания.
Исходные расчетные данные задачи:
N – количество занятий расписания;
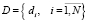 – множество заявок на проведение занятий;
– множество заявок на проведение занятий;
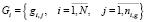 ,
, 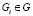 – подмножество групп i-ой заявки;
– подмножество групп i-ой заявки;
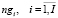 – количество заявок i-ой группы;
– количество заявок i-ой группы;
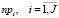 – количество заявок i-ого преподавателя;
– количество заявок i-ого преподавателя;
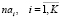 – количество заявок i-ой аудитории.
– количество заявок i-ой аудитории.
Переменные задачи:
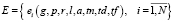 – множество занятий расписания;
– множество занятий расписания;
индекс занятия 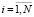 – порядковый номер включения занятия в начальное расписание;
– порядковый номер включения занятия в начальное расписание;
ni, nr – количества включенных и не включенных в начальное расписание занятий;
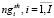 – количество занятий i-ой группы, включенных в начальное расписание;
– количество занятий i-ой группы, включенных в начальное расписание;
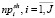 – количество занятий i-ого преподавателя, включенных в начальное расписание;
– количество занятий i-ого преподавателя, включенных в начальное расписание;
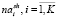 – количество занятий i-ой аудитории, включенных в начальное расписание;
– количество занятий i-ой аудитории, включенных в начальное расписание;
Таблица 1
Оценки загруженности
|
i-ой группы |
i-го преподавателя |
i-ой аудитории |
|
|
|
|
nt – количество таймслотов для включения заявки в начальное расписание занятий;
wk – количество занятий k-ой группы в интервале расписания;
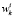 – количество занятий k-ой группы на i-ой «паре» в интервале расписания;
– количество занятий k-ой группы на i-ой «паре» в интервале расписания;
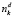 – количество фактических учебных дней k-ой группы в интервале расписания;
– количество фактических учебных дней k-ой группы в интервале расписания;
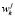 – количество занятий k-ой группы j-ого учебного дня расписания;
– количество занятий k-ой группы j-ого учебного дня расписания;
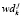 ,
, 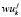 – количество повторяющихся и не повторяющихся по времени занятий k-ой группы в j-ом и (j + 7)-ом учебных днях интервала расписания.
– количество повторяющихся и не повторяющихся по времени занятий k-ой группы в j-ом и (j + 7)-ом учебных днях интервала расписания.
Таблица 2
Оценки равномерности занятий k-ой группы
|
i-ой «пары» |
j-ого учебного дня |
по идентичности занятий в j-ом и (j + 7)-ом учебных днях |
|
|
|
|
Значение оценки 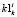 присваивается всем занятиям i-ой «пары» k-ой группы. Значение оценки
присваивается всем занятиям i-ой «пары» k-ой группы. Значение оценки 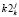 присваивается всем занятиям j-ого учебного дня k-ой группы. Значение оценки
присваивается всем занятиям j-ого учебного дня k-ой группы. Значение оценки 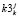 присваивается всем занятиям j-ого и (j + 7)-ого учебных дней k-ой группы.
присваивается всем занятиям j-ого и (j + 7)-ого учебных дней k-ой группы.
Критерий равномерности i-ого занятия расписания:
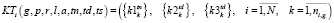 . (7)
. (7)
Критерий равномерности расписания k-ой группы:
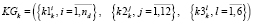 , (8)
, (8)
где nd – количество «пар» в день.
Введем булевы обозначения занятости группы 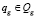 , занятости преподавателя
, занятости преподавателя 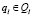 и занятости аудитории
и занятости аудитории 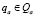 .
.


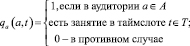
Стратегия SGS1 (формирование начального расписания занятий) состоит в цикличном выборе очередной заявки dni+1 и ее включении в расписание 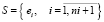 так, чтобы минимизировать критерии равномерности групп последнего включаемого занятия
так, чтобы минимизировать критерии равномерности групп последнего включаемого занятия
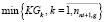 (9)
(9)
при обязательных ограничениях
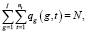 (10)
(10)
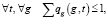
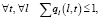
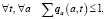 (11)
(11)
Целевая функция (9) обеспечивает наибольшую возможную равномерность занятий групп последней заявки, что достаточно для формирования начального расписания при включении очередного занятия. Условие (10) гарантирует включение всех заявок в начальное расписание. Неравенства ограничений (11) исключают возможность участия любых группы, преподавателя или аудитории более чем в одном занятии формируемого расписания.
SGS1 содержит два правила приоритетов PR11 и PR12, а в каждом цикле осуществляется:
- подготовка исходных данных для правила PR11 – переопределение оценок загруженности групп, преподавателей и аудиторий, а также критериев загруженности заявок занятий, не включенных в начальное расписание;
- в правиле PR11 осуществляется выбор наиболее загруженной заявки занятия среди занятий, не включенных в начальное расписание;
- подготовка исходных данных для правила PR12 – определение критериев равномерности начального расписания в таймслотах для включения выбранной правилом PR11 заявки в начальное расписание занятий;
- в правиле PR12 определяется таймслот для включения выбранной правилом PR11 заявки с обеспечением наибольшей равномерности потребления ресурсов системы.
Рассмотрим применение стратегии SGS1 и правил приоритетов PR11 и PR12.
В начале каждого цикла формирования начального расписания (схема SGS1) перерассчитываются оценки загруженности ресурсов – групп, преподавателей и аудиторий (1–3), на основании которых формируются множества первых, вторых и третьих векторных компонент критериев загруженности заявок.
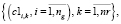 (12)
(12)
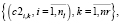 (13)
(13)
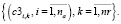 (14)
(14)
Для определения самой загруженной заявки в правиле PR11 применяется многовекторное ранжирование, заключающееся в следующем [2, 4]. Обратное многокритериальное ранжирование векторов (12–14) порождает множества рангов заявок по загруженности групп, преподавателей и аудиторий, формирующие множество векторов рангов заявок
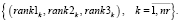 (15)
(15)
Старшая по рангу заявка, полученная прямым многокритериальным ранжированием векторов (15), является самой загруженной при принятых оценках и критериях загруженности. Она становится очередным кандидатом dni+1 на включение в начальное расписание.
Для заявки dni+1 определяется множество всех возможных в соответствии с обязательными ограничениями таймслотов расписания 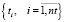 . Оценки равномерности (4–6) групп заявки dni+1 для каждого из таймслотов формируют три множества множеств первых, вторых и третьих многовекторных компонент критериев равномерности.
. Оценки равномерности (4–6) групп заявки dni+1 для каждого из таймслотов формируют три множества множеств первых, вторых и третьих многовекторных компонент критериев равномерности.
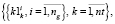 (16)
(16)
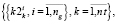 (17)
(17)
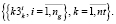 (18)
(18)
Для нахождения таймслота tk, обеспечивающего наибольшую равномерность расписаний групп заявки dni+1, правило PR12 должно реализовать гипервекторное ранжирование критериев равномерности (16–18) заключающееся в следующем.
Прямое многокритериальное ранжирование каждого из множеств векторов (16–18) порождает три множества рангов критериев расписаний каждой группы.
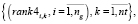 (19)
(19)
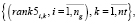 (20)
(20)
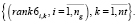 (21)
(21)
Прямое многокритериальное ранжирование каждого из множеств векторов (19–21) порождает три множества рангов занятий для разных таймслотов 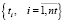 , формирующие множество векторов рангов занятий
, формирующие множество векторов рангов занятий
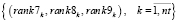 . (22)
. (22)
Прямое многокритериальное ранжирование векторов (22) определяет доминирующий вектор, индекс k которого определяет искомый таймслот, в котором будет проводиться занятие заявки dni+1. Если nr > 0, то переход к следующему шагу формирования начального расписания.
Стратегия SGS2 (оптимизация расписания занятий) состоит в цикличном выборе очередного занятия и изменении расписания 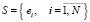 , которое минимизирует критерии равномерности групп последнего переставляемого занятия (9) при обязательных ограничениях (11).
, которое минимизирует критерии равномерности групп последнего переставляемого занятия (9) при обязательных ограничениях (11).
В схеме SGS2 используются два правила приоритетов PR21 и PR22. Правило PR22 эквивалентно правилу PR12, поэтому в каждом цикле SGS2 осуществляется:
- подготовка исходных данных для правила PR21 – переопределение оценок равномерности расписаний групп, а также критериев равномерности занятий расписания;
- в правиле PR21 осуществляется выбор наиболее неравномерного занятия расписания;
- дальнейшие действия совпадают с действиями схемы SGS1.
Рассмотрим применение стратегии SGS2 и правила приоритетов PR21
В начале каждого цикла оптимизации расписания перерассчитываются оценки равномерности групп, на основании которых формируются множества первых, вторых и третьих векторных компонент критериев равномерности занятий.
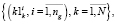 (23)
(23)
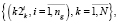 (24)
(24)
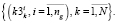 (25)
(25)
Для определения самого неравномерного занятия в правиле PR21 применяется многовекторное ранжирование, заключающееся в следующем. Многокритериальное ранжирование векторов (23–25) порождает множества рангов занятий, формирующие множество векторов рангов
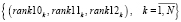 . (26)
. (26)
Старшее по рангу занятие, полученное многокритериальным ранжированием векторов (26), является самым неравномерным при принятых оценках и критериях равномерности и становится очередным кандидатом на перестановку в расписании. Далее, как и в схеме SGS1, для множества всех возможных в соответствии с обязательными ограничениями таймслотов расписания определяется искомый таймслот для перестановки.
Заключение
Автор считает новыми следующие положения и результаты:
– введены многовекторные критерии загруженности заявок и равномерности занятий расписания;
– разработан общий подход к формированию расписания занятий вуза на основе двух последовательно применяемых схем генерации расписаний;
– использование правил приоритетов базируется на методах ранжирования теории принятия решений.




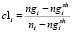 (1)
(1)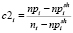 (2)
(2)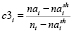 (3)
(3)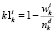 (4)
(4)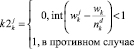 (5)
(5)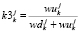 (6)
(6)