Продолжающееся масштабирование в современных субмикронных технологиях вызывает трудности проектирования цифровых интегральных схем (ИС). Возрастание технологических отклонений (ТО), характерных для 28 и более низких нанометровых технологий, усложняет процесс верификации результатов проектирования ИС. Как известно, развитие интегральных схем направлено на улучшение следующих основных параметров – уменьшение площади кристалла, расходов потребляющей мощности, напряжения питания, порогового напряжения, размеров отдельных электрических и геометрических компонентов [1]. Неучет ТО во время проектирования и верификации приводит к неисправности ИС, возрастанию вероятности возвращения с производства на проектирование, а также к другим негативным явлениям и, как следствие, к уменьшению процента выхода годных и, следовательно, прибыли [2]. Как правило, средства, предназначенные для уменьшения ТО, приводят к резкому возрастанию площади, потреблению тока, что и усложняет проектирование [3]. После проектирования ИС производится, но в каждой ИС происходят отклонения значений параметров, из-за неидеальности производящих приборов и процессов производства [4]. Кроме этого, каждая ИС находится в отдельной рабочей среде, в зависимости от места и цели использования. Факторы рабочей среды (температура, напряжение питания, рабочая нагрузка), влияя на ИС, меняют значения ее параметров. Чтобы ИС соответствовала техническим заданиям, необходимо, чтобы проектировщик учел все указанные факторы.
Основным методом временного анализа (ВА) цифровых ИС является статический временной анализ (СВА), так как потребляемое время с увеличением размеров ИС увеличивается линейно [5]. При СВА схема разбивается на отдельные пути, после этого производится анализ времен установления и удержания. Для моделирования МС разбросов используется метод наилучших (НЛ) и наихудших (НХ) случаев, когда все транзисторы внутри одного ИС одновременно имеют самую большую или самую маленькую задержку. Однако с возрастанием влияния ТО эффективность этого метода резко уменьшается, так как разбросы параметров транзисторов уже не монотонны и не гарантируют получения крайних значений задержек. Для этого нужно учитывать десятки и даже сотни комбинаций разных параметров, что связано с большими затратами как машинных, так и человеческих ресурсов.
В современных интегральных схемах единственным продуктивным способом учета ТО является использование статистических моделей, когда каждому параметру присваивается не отдельное значение отклонения, а разброс, описываемый рассеиванием. Несмотря на то, что для отдельных транзисторов существуют такие модели, для оценки задержки в цифровых ИС их непосредственное использование нецелесообразно. Причинами являются необходимость больших машинных ресурсов и временных затрат, а также невозможность применения этих моделей в типовом маршруте проектирования цифровых ИС.
В данной статье предлагается метод улучшения статистического статического временного анализа (ССВА) при учете в структурных корреляциях.
К основным операторам, используемым во время статистического статического временного анализа (ССВА), относятся операторы суммирования и максимума статистических данных (ССД и МСД) [6]. ССД используется во время суммирования задержки стандартной ячейки с входным временем поступления, а МСД – для выбора максимальной задержки на выходе многовходовой ячейки [7]. Для двухвходовой ячейки «И» с входами i, j и выходом o задачу СВА можно сформулировать в виде [8]:
A0 = max(Ai + Di0, Aj + Dj0), (1)
где Ai, Aj и A0 – времена поступления сигналов соответственно на входы и выход; Di0 и Dj0 – задержки от входов до выхода.
Известно, что если Am – максимум входных времен поступлений Ai и Aj, то функция интегрального распределения [9] (ФИР) Am может быть представлена в виде
Cm(t) = Ci(t)•Cj(t), (2)
где Ci(t) и Cj(t) – ФИР переменных Ai и Aj. Важно отметить, что (2) действительно только в случае независимости переменных Ai и Aj и только при использовании ФИР.
Но в действительности в структурах цифровых схем почти всегда бывают случаи, когда пути, которые начинаются с одной точки, разделяются, а потом снова соединяются, вызывая структурные корреляции. На рис. 1 показан пример такой схемы. Для этого случая (2) больше не действует.
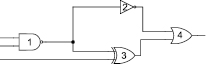
Рис. 1. Пример схемы со сходящимися разветвлениями
Здесь времена поступления на входы ячейки «4» зависимы от выхода «1». В таком случае имеет место структурная корреляция, когда отклонение задержки общей части влияет на ячейки «2» и »3», а потом – и на выход «4». Это приводит к излишнему пессимизму при оценке отклонения задержки [6]. Время поступления на выход определяется с помощью (3). Если Ai = Ac + D1, а Aj = Ac + D2, где Ac – общая часть задержки, а D1 и D2 – отдельные части, то с учетом того, что Ac имеет константное значение, выражение (3) можно преобразовать следующим образом:
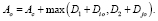 (3)
(3)
Поскольку переменные D1, Dio, D2 и Dio независимы, то с использованием (2) выражение (3) можно представить в виде
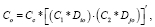 (4)
(4)
где Сс, С1 и С2 – ФИР общей и отдельных частей соответственно. Полученное уравнение помогает учитывать корреляции, но только при простых схемах, когда один выход имеет два разветвления. На практике схемы и зависимости более сложны (рис. 2).
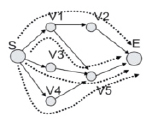
Вход ячейки «C5» зависит от соединений A, B, C и D. Каждое из них формулирует определенные подпути к входу «C5». Для вычисления времени поступления на выходе следует учитывать все эти зависимости. Предложенный алгоритм вычисления времени поступления с учетом структурных корреляций приведен на рис. 3.
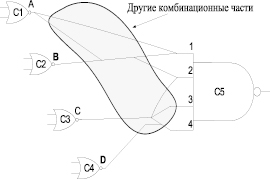
Рис. 2. Общий случай сходящихся разветвлений в цифровых ИС
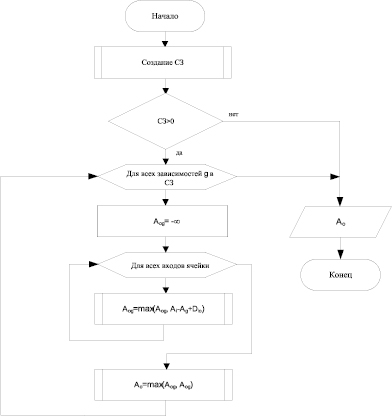
Рис. 3. Предложенный алгоритм вычисления времен поступления с учетом структурных корреляций
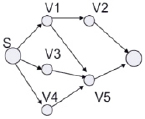
а) б)
Рис. 4. Иллюстрация метода решения МСД для отдельных ячеек (а) и путей (б)
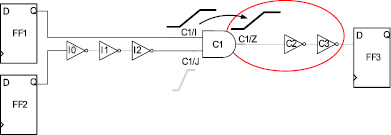
Рис. 5. Иллюстрация выбора максимального фронта для отдельных ячеек
Предлагается создать список зависимостей (СЗ), где бы сохранились все вершины соответствующего графа схемы и список вершин, от которого зависит данная вершина. В списке вершины сортируются согласно их уровням, то есть самые близкие вершины соответствуют самому высокому уровню. Так как использование полного СЗ связано с большими машинными затратами, дается возможность ограничить его способом удаления вершин с нижних уровней СЗ. Используя алгоритм для рис. 3, первый и третий входы «C5» будут рассматриваться зависимыми только от B, а второй и четвертый – от C, так как B и C находятся на более высоком уровне в СЗ. После этого времена поступления вычисляются с помощью (4) и, как независимые переменные, используются в (2) для решения МСД. При вычислении МСД использован метод, основанный на отдельном вычислении максимума для каждой ячейки (рис. 4, а). Это позволяет сократить машинное время в среднем в три раза по сравнению с методом вычисления МСД всех путей (рис. 4, б). Несмотря на то, что данный метод позволяет уменьшить временные затраты, он более пессимистичен с точки зрения оценки задержки схемы.
На рис. 5 показан пример схемы с многовходовой ячейкой. При выборе максимального фронта на входе «C1» выбирается фронт входа I, который будет дальше распространяться в схеме и определять дальнейшие значения задержек. От этих значений зависит выбор критического пути схемы. Если в конечном итоге критическим путем окажется путь от FF2 до FF3, то эта оценка будет пессимистичной, так как в рабочем режиме фронт сигнала от FF2 до FF3 более короткий.
С целью уменьшения пессимизма оценки предложена методика, позволяющая в вышеописанных случаях перейти к отдельному вычислению МСД для определенных критических путей.
Выполняется перерасчет времени для отдельного пути, в результате чего временной запас для данного критического пути увеличивается. Это, в свою очередь, сокращает число итераций от ВА до проектирования и ручных изменений схемы. Данная методика перерасчета временных задержек эффективна в случае больших схем, так как вероятность пессимистичного вычисления МСД увеличивается с ростом сложности схемы.
Таблица 1
Точность учета структурных корреляций по сравнению с другими методами
|
Схема |
Задержка, пс |
Ошибка по сравнению с HSPICE, % |
|||
|
Метод 1 [6] |
HSPICE |
Предложенный метод |
Метод 1 |
Предложенный метод |
|
|
C432 |
758 |
770 |
741 |
1,56 |
3,77 |
|
C1908 |
1387 |
1426 |
1350 |
2,73 |
5,33 |
|
C2670 |
1749 |
1795 |
1711 |
2,56 |
4,68 |
|
C3540 |
4181 |
4278 |
4062 |
2,26 |
5,04 |
|
C7552 |
8640 |
8863 |
8377 |
2,51 |
5,48 |
Таблица 2
Сравнение быстродействия учета структурных корреляций
|
Схема |
Быстродействие, раз |
|
|
По сравнению с методом 1 |
По сравнению с HSPICE |
|
|
C432 |
2,30 |
3,20 |
|
C1908 |
2,61 |
3,25 |
|
C2670 |
2,45 |
4,45 |
|
C3540 |
2,19 |
5,41 |
|
C7552 |
4,52 |
6,17 |
Выводы
Сравнение точности и быстродействия структурных корреляций данного метода приведено в табл. 1 и 2. Для сравнения были выбраны схемы из набора ISCAS-89.
Эффективность предложенного в статье метода была сравнена с программной реализацией на данный момент широко используемым методом 2, а также была сравнена с результатами моделирования HSPICE Монте-Карло, когда учитываются структурные корреляции.
Предлагаемый подход вычисления структурной корреляции позволяет при допустимой точности значительно увеличить скорость расчета временных проверок.



