Цифровая обработка сигналов (ЦОС) относится к числу наиболее динамически развивающихся областей инженерной деятельности [2, 8, 10]. Медицина, системы сотовой связи, телекоммуникации, Internet-технологии, обработка звука и изображений, навигация – вот далеко не полный перечень приложений, в которых активно используются методы ЦОС. В настоящее время широкое применение нашли специализированные процессоры (СП) цифровой обработки сигналов, которые базируются на реализации ортогональных преобразований сигналов. Такие ортогональные преобразования сигналов, как правило, определены над полем комплексных чисел. Среди таких преобразований сигналов можно выделить быстрые преобразования Фурье (БПФ) [1, 4, 9]. Однако они имеют ряд недостатков, которые связаны с наличием двух вычислительных трактов для обработки действительной и мнимой части сигнала, а также с ошибками округления, вызванных использованием в качестве поворачивающих коэффициентов функций синусов и косинусов. Поэтому разработка новых алгоритмов ортогональных преобразований сигналов с использованием целочисленной арифметики, позволяющих устранить отмеченные недостатки, является актуальной задачей.
Цель исследования
Основным недостатком ортогональных преобразований сигналов на основе БПФ является использование в качестве ортогональных базисов тригонометрических функций. Решить данную проблему можно за счет перехода к целочисленному вычислению. В работах [1, 3, 5, 7] предлагается выполнять цифровую обработку сигнала с использованием теоретико-числовых преобразований (ТЧП). Однако такие целочисленные преобразования сигналов имеют малую производительность, так как они подобны дискретному преобразованию Фурье (ДПФ). Поэтому целью работы является повышение скорости выполнения ортогональных преобразований сигналов за счет разработки быстрого алгоритма ТЧП.
Материалы и методы исследования
В настоящее время конечные поля Галуа нашли применение в цифровых телекоммуникационных системах в основном в направлениях, связанных с построением корректирующих кодов, а также с формированием псевдослучайных последовательностей. Использование конечных полей для задач цифровой обработки сигналов ограничено из-за отсутствия критериев существования быстрых алгоритмов вычисления теоретико-числовых преобразований, являющихся альтернативой преобразованию Фурье. Указанное ограничение обусловлено тем, что в отличие от комплексного случая, в модулярной арифметике, не существуют примитивные (первообразные) корни из единицы любой степени. Поэтому разработка алгоритмов быстрого вычисления ТЧП и критериев их существования, позволит повысить эффективность работы инфокоммуникационных систем.
Для многих практических приложений ЦОС используется быстрое преобразование Фурье. При реализации БПФ возможны несколько вариантов организации вычислений в зависимости от способа деления последовательности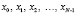 
длины N на части. В случае четного N возможно использование варианта «прореживания по времени», который определяется как сумма двух 
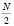точечных дискретных преобразований Фурье
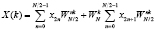, (1)
где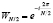 
, 
, 
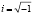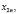
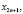– подпоследовательности длины 
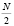с четными и нечетными номерами соответственно. Из равенства (1) видно, что реализация БПФ характеризуется наличием двух вычислительных трактов, влияющих на схемные затраты и надежность спецпроцессора ЦОС. Кроме того, БПФ в качестве поворачивающих коэффициентов использует иррациональные числа, что снижает точность вычислений. Устранить данные недостатки возможно за счет использования ТЧП, определенного в алгебраической системе, обладающей свойствами кольца или поля [2, 6, 10].
Пусть GF(M) – конечное поле Галуа, GN – циклическая группа порядка N,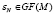 
– примитивный корень порядка N (εN элемент поля GF(M), удовлетворяющий условию 
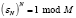и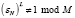 
для любого натурального L < N). Тогда ТЧП последовательности 
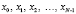, где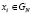 
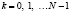имеет вид
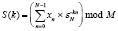, (2)
Обратное теоретико-числовое преобразование имеет вид
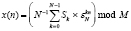. (3)
Очевидно, что ТЧП по своей структуре наилучшим образом реализуются с использованием цифровой элементной базы. Например, если взять εN в виде степени двойки, то умножение в (2) и (3) на степени εN при вычислении ТЧП заменяется сдвигами кодовых слов и приведением сдвинутых кодовых слов по модулю числа М [2].
В работе [10] показана возможность повышения скорости выполнения ТЧП за счет использования разработанного алгоритма применения модулярных кодов. Если в качестве числа M использовать составные числа Мерсена, то выражения (2) и (3) можно свести к многомерной параллельной обработке.
Свойства ТЧП изоморфны свойствам дискретного преобразования Фурье. Следовательно, должна существовать возможность вычисления ТЧП с использованием быстрых алгоритмов, аналогичных БПФ. Перенесем подходы, используемые при построении БПФ с прореживанием по времени из поля комплексных чисел (1) в конечное поле Галуа GF(M). Принимая во внимание (1), перепишем (2) в виде:
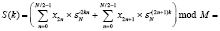
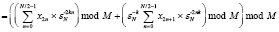. (4)
Из выражения (4) вытекает условие разложения N точечного ТЧП в сумму двух ТЧП длины N/2. Рассмотрим следующую теорему.
Теорема. Пусть GF(M) – конечное поле Галуа, N – четное число, GN – циклическая группа порядка N,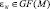 
– примитивный корень порядка N, удовлетворяющий
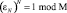. (5)
Тогда ТЧП последовательности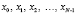 
, где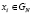 
представимо в виде суммы ТЧП подпоследовательностей с четными 
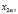и нечетными 
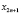номерами.
Доказательство. Из условия (5) следует существование примитивного корня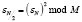 
порядка N/2. Преобразуем выражение (4) с учетом равенства (5):
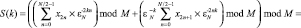
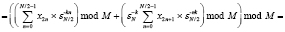
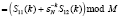, (6)
где S11(k) и S12(k) – ТЧП последовательностей с четными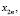 
и нечетными 
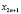номерами.
Так как S11(k) и S12(k) имеют размерность N/2, формулу (6) можно использовать только для вычисления S(k) при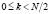 
. Для случая следует воспользоваться периодичностью ТЧП:
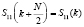и 
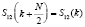. (7)
С учетом (7) при условии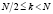 
формулу (6) можно переписать в виде
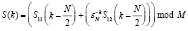. (8)
Теорема доказана.
В отличие от БПФ в поле комплексных чисел, в котором существуют корни из единицы любой степени (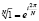
, 
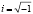), условие представления размерности ТЧП в виде степени двойки не является достаточным для существования быстрого ТЧП с «прореживанием по времени» ввиду отсутствия в конечных полях корней из единицы любой степени. Рассмотрим примеры использования доказанной теоремы.
Результаты исследования и их обсуждение
Воспользуемся для вычисления ТЧП сигнала конечные поля GF(17), GF(29). При этом в поле GF(17) длина входной последовательности равна 16 отсчетам, а в конечном поле GF(29) – длина входного вектора будет составлять 28 отсчетов.
Пример 1. Выполним теоретико-числовое преобразование вектора (x0, x1, x2, ..., x15) = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15) в поле GF(17), для чего подготовим цепочку примитивных корней: ε16 = 3, ε8 = 9, ε4 = 13, ε2 = 16. Заметим, что подобранные числа удовлетворяют условию
, 
, 
.
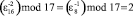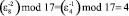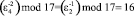На первом этапе разработанного быстрого алгоритма ТЧП по модулю 17 получаем
; 
;
; 
;
.
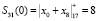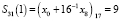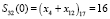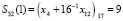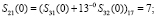
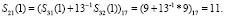
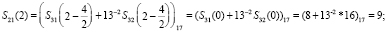
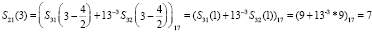Аналогичным образом получаются остальные спектральные составляющие ТЧП. Структура и конкретные значения 16-точечного ТЧП представлена на рис. 1.
Пример 2. Вычислим ТЧП входного вектора отсчетов (x0, x1, x2, ..., x15, x27) = (0, 1, 2, ..., 26, 27) в конечном поле Галуа GF(29). Для этого необходимо вычислить следующую цепочку примитивных корней: ε28 = 2, ε14 = 4, ε7 = 16. Структура и конкретные значения 28-точечного ТЧП представлены на рис. 2.
Сформулированные в работе условия разложимости N-точечного ТЧП на преобразования меньшей размерности и доказательство теоремы позволяют разрабатывать быстрые алгоритмы ТЧП вычисления ортогональных преобразований сигналов в конечных полях. Это было продемонстрировано на примерах 1 и 2. Наиболее эффективны быстрые алгоритмы ТЧП в случае, когда длина вектора исходных данных является степенью двойки и выполнены условия (5). В этом случае деление последовательностей на две части можно продолжать до тех пор, пока не получатся двухэлементные последовательности, что было показано в примере 1.
Оценим эффективность быстрого алгоритма ТЧП с прореживанием по времени, обусловленную разложением N-точечного преобразования на несколько малых. Для вычисления N-точечного ТЧП по формуле (2) требуется N2 операций. Наибольшая степень ускорения вычислений может быть достигнута при N = 2k и существовании примитивного корня порядка N. Число требуемых при этом операций можно оценить как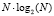 
. Таким образом, вычислительные затраты по сравнению с непосредственным использованием формулы (2) уменьшаются в 
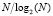раз.
Заключение
Основное преимущество ТЧП по сравнению с ДПФ состоит в том, что корни из единицы имеют простое представление, что позволяет в вычислениях заменить комплексную арифметику на целочисленную. Использование быстрых ТЧП с прореживанием по времени имеет смысл, если число элементов в анализируемой последовательности является степенью 2 и только при существовании в конечном поле GF(M) примитивного корня порядка длины анализируемой последовательности. В этом случае разработанный алгоритм быстрого ТЧП сигнала не является приближенным алгоритмом, причем ускорение достигается исключительно за счет оптимальной организации вычислений.
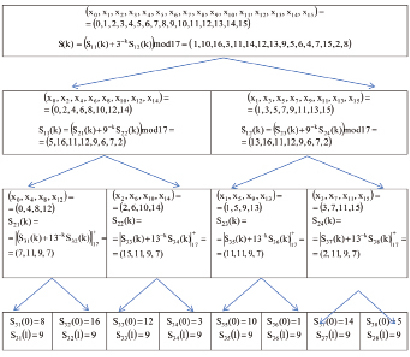
Рис. 1. Структура быстрого ТЧП по модулю 17 при N = 16
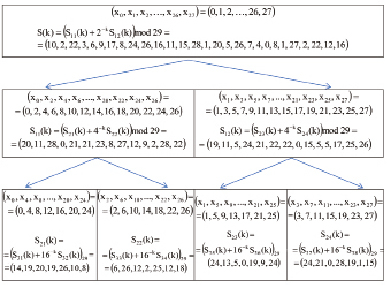
Рис. 2. Структура быстрого ТЧП по модулю 29 при N = 28
Разработанный алгоритм быстрого выполнения ТЧП сигнала с прореживанием по времени предназначен для одновременного расчета всех спектральных коэффициентов S(k). Если необходимо получить значения коэффициентов для некоторых k, предпочтительнее использовать прямую формулу ТЧП.