Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Одним из инновационных направлений развития легкой промышленности является внедрение нанотехнологий. Некоторые вопросы разработки наномодифицированных материалов и изделий из них отражены в работах [1–3]. Актуальность работы обусловлена тем, что оценить наличие наночастиц на поверхности текстильных материалов и тем более определить их принадлежность к серебру или золоту трудно из-за их малого количества [4–5]. Решение данной проблемы возможно при применении многомерных методов оценки достоверности по поляризационным характеристикам и составляющим рамановских спектров.

Математическая обработка рамановских спектрограмм возможна только при использовании информационных технологий, современных прикладных программных продуктов, обеспечивающих обработку большого массива данных с высокой точностью.

Цель работы – разработка алгоритма и программной реализации математического моделирования рамановских спектров наномодифицированных текстильных материалов.

Материалы и методы исследования

Для реализации поставленной цели разработана программа проведения исследований, которая включает следующие этапы:

1. Обработка материалов наночастицами серебра, золота.

2. Получение рамановских спектров текстильных материалов.

3. Математическая обработка полученных рамановских спектрограмм.

4. Разработка компьютерной реализации математической модели рамановских спектров.

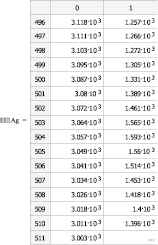
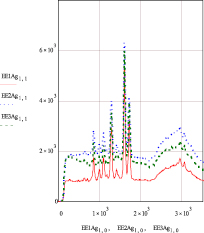
При проведении эксперимента выбраны полиэфирные (ПЭ) волокна, на которые были нанесены наночастицы серебра из коллоидного раствора наночастиц серебра AgБион – 2 (ТУ 2499-003-44471019-2006, концерн «Наноиндустрия»), а также наночастицы золота из коллоидного раствора наночастиц золота (ТУ 9154-001-93099853-06 НПО БИОТЕСТ). Измерения были проведены на сканирующем зондовом микроскопе (СЗМ) с конфокальным рамановским и флюоресцентным спектрометром OmegaScope™ – в региональном центре нанотехнологий Юго-Западного государственного университета. На каждом образце были проведены измерения с поляризацией лазерного луча вдоль и поперек волокон. Перевод рамановских спектрограмм из программы Spekwin32 в Mathcad осуществлялся через Excel compatible ASCII. В результате были получены 751 цифровое значение параметров рамановских спектрограмм наночастиц серебра и золота. На рис. 1 представлены выборочные фрагменты 16 цифровых значений параметров рамановских спектрограмм (для l = 496..511). При этом на рис. 1, а – для наночастиц серебра при поляризации луча вдоль волокон в первой серии экспериментов, на рис. 1, б – для наночастиц золота при поляризации луча поперек волокон в первой серии экспериментов. В представленных матрицах цифровых параметров столбец 0 соответствует волновым числам спектрограммы, столбец 1 – интенсивности спектра. На основании цифровых значений в программе Mathcad построены рамановские спектрограммы. На рис. 2 представлены рамановские спектрограммы для всех 751 цифровых значений (l = 0..750), снятые в трех сериях экспериментов. На рис. 2, а – для наночастиц серебра с поляризацией луча вдоль волокон, на рис. 2, б – для наночастиц серебра с поляризацией луча поперек волокон.

Из рис. 2 видно, что наблюдается значительное отклонение спектрограмм от оси х, на основании чего можно сделать вывод, что в спектрограммах присутствует фоновая люминесцентная составляющая, которую необходимо учесть при обработке спектров [6–7]. Для этого была произведена оцифровка фоновых составляющих по 26 точкам и получены соответствующие матрицы для наночастиц серебра: Af1-Af3 – с поляризацией вдоль волокон; Af4-Af6 – с поляризацией поперек волокон и для наночастиц золота: AfAu1-AfAu3 – с поляризацией вдоль волокон; AfAu1-AfAu3 – с поляризацией поперек волокон.

Аналитический вид фоновых люминесцентных составляющих спектрограмм в работе представлен математической моделью (1), которая была получена регрессией с использованием нескольких отрезков полинома, реализуемой комбинацией встроенных функций программы Mathcad loess и interp:

A(t):=interp(loess(X,Y,k), X,Y,t), (1)

где s:= loess(X,Y,k) – вектор коэффициентов для построения аппроксимирующего полинома второй степени; interp(s,X,Y,t) – результат полиномиальной регрессии; X – вектор значений аргумента; Y – вектор значений функции; k – параметр, определяющий размер отрезков полиномов; t – значение аргумента, при котором вычисляется интерполирующая функция.

При реализации данного метода в системе Mathcad предложена следующая программная реализация в общем виде:

X_ii:=Af_ii,0 Yii:=Af_ii,1

k:=0.3

s:=loess(X,Y,k)

A(t):=interp(s,X,Y,t). (2)

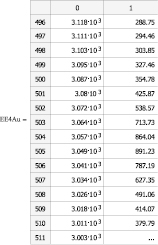 а   б

Рис. 1. Цифровые значения рамановских спектрограмм наночастиц серебра, золота

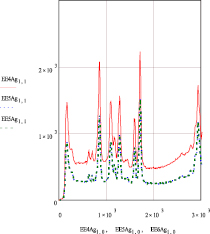 а   б

Рис. 2. Спектрограммы рамановского комбинационного рассеяния света

В данном случае в качестве аргумента X выступают значения волновых чисел из столбца 0 матриц Af, полученных в результате оцифровки спектрограмм, а в качестве аргумента Y – значения интенсивности из столбца 1 матриц Af, полученных в результате оцифровки спектрограмм. Данную программу необходимо применить для всех спектров, полученных в работе.

Для программной реализации предложенного метода был составлен алгоритм проведения математического моделирования составляющих рамановских спектров, представленный на рис. 3.

Особенностью алгоритма, представленного на рис. 3, является наличие циклических вычислений для определения коэффициентов полиномиальной модели. Для решения данной задачи можно использовать встроенный язык программирования системы Mathcad, в котором имеется оператор цикла for.

Программная реализация циклического вычисления корней уравнения с использованием функции loess имеет вид

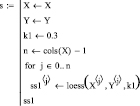
Программная реализация алгоритма в программе Mathcad реализована при проведении моделирования рамановских спектров полиэфирных волокон при нанесении на них наночастиц серебра, золота.

Результаты исследования и их обсуждение

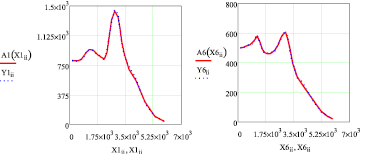
Для анализа результатов математического моделирования фоновых составляющих рассмотрим выборочные графические зависимости, представленные на рис. 4. На рис. 4, а, изображены экспериментальная зависимость Y1ii от X1ii значений фоновых составляющих спектрограмм с наночастицами серебра при поляризации вдоль волокон, полученных в результате оцифровки по 26 точкам, и теоретическая зависимость А1(Х1ii) от X1ii значений фоновых составляющих спектрограмм с наночастицами серебра при поляризации вдоль волокон, полученных по результатам моделирования по модели (2) по 26 точкам. На рис. 4, б, изображены экспериментальная зависимость Y6ii от X6ii значений фоновых составляющих спектрограмм с наночастицами серебра при поляризации поперек волокон, полученных в результате оцифровки по 26 точкам, и теоретическая зависимость А6(Х6ii) от X6ii значений фоновых составляющих спектрограмм с наночастицами серебра при поляризации поперек волокон, полученных по результатам моделирования по модели (2) по 26 точкам.

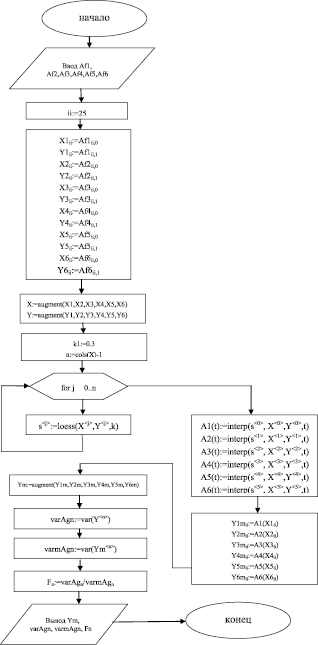
Рис. 3. Алгоритм проведения математического моделирования

а б

Рис. 4. Фоновые люминесцентные составляющие рамановских спектрограмм

а б

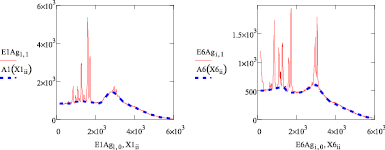
Рис. 5. Совместные графические данные смоделированных фоновых люминесцентных составляющих спектрограмм и начальных спектрограмм

Совмещение смоделированных фоновых люминесцентных составляющих с рамановским спектром представлено на рис. 5. Соответственно для спектров с наночастицами серебра с поляризацией вдоль волокон (рис. 5, а) и поперек волокон (рис. 5, б). Визуальный анализ показывает достаточно высокую точность аппроксимации.

Универсальность предложенной математической модели (2) заключается в том, что в зависимости от подставляемого аргумента t в выражение A(t) можно моделировать различное число значений. Так, при использовании в качестве аргумента t в данной модели реального количества экспериментальных значений параметров спектрограмм (в нашем случае 751) можно смоделировать также 751 значение параметров фоновых составляющих. Таким образом, используя предложенную в работе математическую модель по 26 исходным значениям, были смоделированы параметры фоновых составляющих по реальному количеству данных равных 751. При этом использованы следующие обозначения параметров:

– значения интенсивности фоновой составляющей спектрограммы с наночастицами серебра при поляризации вдоль (А1(Х1ii), А2(Х2ii), А3(Х3ii)) поперек (А4(Х4ii), А5(Х5ii), А6(Х6ii)) волокон, полученных по результатам моделирования по модели (2) по 26 точкам в первой – третьей повторности соответственно;

– значение интенсивности фоновой составляющей спектрограммы с наночастицами серебра при поляризации вдоль (А1(E1Agi,0), А2(E2Agi,0), А3(E3Agi,0)) и поперек (А4(E4Agi,0), А5(E5Agi,0), А6(E6Agi,0)) волокон, полученных по результатам моделирования по модели (2) по 751 точке в первой – третьей повторности соответственно;

– значение интенсивности фоновой составляющей спектрограммы с наночастицами золота при поляризации вдоль (А1Au(ХAu1ii), А2Au(ХAu2ii), А3Au(ХAu3ii)) и поперек (А4Au(ХAu4ii), А5Au(ХAu5ii), А6Au(ХAu6ii)) волокон, полученных по результатам моделирования по модели (2) по 26 точкам в первой – третьей повторности соответственно;

– значение интенсивности фоновой составляющей спектрограммы с наночастицами золота при поляризации вдоль (А1Au(E1Aui,0), А2Au(E2Aui,0), А3Au(E3Aui,0)) и поперек (А4Au(E4Aui,0), А5Au(E5Aui,0), А6Au(E6Aui,0)) волокон, полученных по результатам моделирования по модели (2) по 751 точке в первой – третьей повторности соответственно.

Адекватность полученных математических моделей была проверена по критерию Фишера и представлена в таблице.

Проверка математических моделей на адекватность

В результате можно констатировать, что математические модели фоновых составляющих, реализованные в программе Matchcad, являются адекватными.

Выводы

1. С учетом большого разброса значений информационных параметров при идентификации наночастиц серебра и золота на текстильных материалах предложен метод математической обработки параметров фоновых флюоресцирующих составляющих спектрограмм с информационной неопределенностью при принятии решения о наличии наночастиц.

2. Сложность проведения математической обработки спектрограмм возникает в том, что оцифровка фоновой составляющей производится по 26 точкам с параметром Xii, а данных в спектре Еi,j при i = 0…750, поэтому возникает необходимость специального математического моделирования фоновых люминесцентных составляющих спектрограмм.

3. Фоновая составляющая выделена математическим моделированием данных по многомерной регрессии по 26 точкам с последующей интерполяцией и приближением к исходной спектрограмме с количеством точек i = 0…750.

Таким образом, в работе разработана математическая модель фоновых составляющих рамановских спектрограмм при аппроксимации массива данных отрезками нескольких полиномов и реализована программная реализация данного метода в системе Mathcad.