Решение задачи дифракции волн опирается на решение волнового уравнения при заданных граничных условиях. Дифракция волн на объектах с реальными поверхностями – статистическая задача, решение которой должно определить статистические характеристики рассеянного излучения и установить их связь со статистическими характеристиками поверхности [1–3]. При измерении характеристик аэро- и гидродинамических потоков требуется учитывать характеристики и свойства поля излучения, рассеянного малыми частицами [4, 5].
Вопросы влияния структуры поля рассеянного излучения на процесс образования интерференционной картины рассматриваются в работах по голографической интерферометрии [6, 7]. Однако методы голографической интерферометрии, как правило, используют информацию о результатах сравнения структуры волновых фронтов излучения, рассеянного объектом в статических состояниях.
Исследованию влияния движения объекта на процесс регистрации интерференционной картины посвящен ряд работ [8–11]. Но в них либо исследуются методы устранения влияния движения на результаты регистрации, либо рассматривается движение точечного рассеивателя. Однако предметом исследования зачастую являются волновые поля более сложные, чем поля со сферическими или плоскими волновыми фронтами. Освоение всё более коротковолнового электромагнитного излучения и необходимость производить измерения параметров движения объектов, удаленных на малые расстояния, приводят к ситуации, когда исследуемый объект уже нельзя считать точечным. В этих случаях доплеровские методы в целях эффективного усреднения регистрируемого неоднородного поля по спектру пространственных частот для достижения необходимого отношения сигнала к шуму предполагают фокусирование электромагнитного излучения на исследуемый объект и предельное уменьшение размеров входных апертур регистрирующих устройств (например, [12]). Последние обстоятельства приводят к ухудшению энергетических и других характеристик измерителей радиальной скорости обычными доплеровскими методами. Измерение же полного вектора скорости становится тем более затруднительным.
В то же время остается до конца не решенным вопрос использования для измерения параметров движения информации об изменении пространственно-временной структуры волновых фронтов рассеянного движущимся объектом электромагнитного излучения. Данная проблема требует, прежде всего, выработки физических представлений и математических моделей механизмов рассеяния электромагнитного излучения на поверхности реальных движущихся объектов, о свойствах получающегося рассеянного поля и о влиянии данных свойств на образование интерференционной диаграммы.
Целями работы являются:
– построение математической модели структуры волнового поля излучения, рассеянного движущимся объектом, и оценка влияния этой структуры на характеристики сигнала квадратичного приемника, производящего усреднение регистрируемой интерференционной диаграммы по спектру пространственных частот;
– на основе результатов предыдущего пункта построение математической модели регистрируемого рассеянного излучения с сохранением информации о его фазовых характеристиках пространственно распределенной регистрирующей структурой, обладающей интегрирующими во времени свойствами;
– выявление принципиальных различий и общих свойств рассмотренных способов регистрации рассеянного излучения.
Для решения задачи дифракции электромагнитного излучения на движущемся объекте со статистически неровной поверхностью используем метод Кирхгофа. Поле в произвольной точке пространства связано с полем на поверхности исследуемого объекта формулой дифракции Релея – Зоммерфельда:
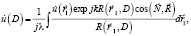(1)
где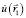 
– поле в произвольной точке 
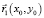на исследуемой поверхности, R – расстояние от этой точки до точки D, в которой вычисляется поле 
.
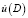Допустим, что средняя плоскость статистически шероховатой поверхности совпадает с плоскостью z = 0 (рис. 1) прямоугольной системы координат x0, y0, z, а уравнение поверхности задано в виде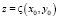 
, где ς будем считать статистически стационарной, дифференцируемой требуемое число раз функцией. Пусть на эту поверхность падает плоская монохроматическая волна, потенциал которой запишем в ви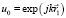де 
, где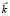 
– волновой вектор падающей волны.
Здесь и далее будем опускать множитель, выражающий амплитуду падающей волны, и временной множитель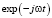 
, где ω – циклическая частота падающей волны. Будем считать, что плоскость входной апертуры регистрирующего устройства расположена в плоскости z = z0, совпадающей с плоскостью xy прямоугольной системы координат xyz, а регистрирующее устройство представляет собой квадратичный приемник, сигнал на выходе которого пропорционален интегральной интенсивности поля на поверхности входной апертуры:
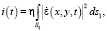(2)
где η – коэффициент пропорциональности,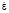 
– результирующее распределение комплексных амплитуд поля на поверхности апертуры, площадь которой S1.
Рассмотрим случай, когда устройство, регистрирующее излучение, рассеянное движущимся шероховатым объектом, находится в зоне Фраунгофера, то есть на расстоянии большем по сравнению с размерами рассеивающей поверхности. Воспользуемся решением для потенциала рассеянного поля в виде формулы Грина [1]:
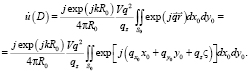(3)
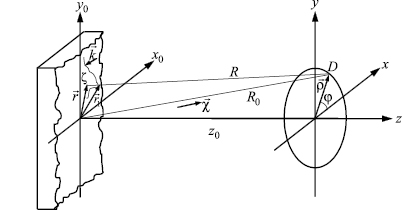
Рис. 1. К исследованию влияния поля, рассеянного объектом с шероховатой поверхностью, на характеристики сигнала квадратичного приемника
В формуле (3) V – коэффициент отражения (в электромагнитной задаче – френелевский коэффициент), который можно считать величиной постоянной во всех практически интересных случаях [1], вектор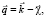 
где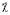 
– вектор, направленный из начала координат в точку наблюдения и равный по модулю волновому числу k падающей волны, R0 – расстояние от центра координат до точки наблюдения. Интегрирование в (3) ведется по площади S0 средней плоскости шероховатой поверхности.
Введем следующие ограничения для упрощения преобразований без потери общности выводов:
- волновой вектор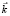 
падающей волны лежит в плоскости x0z;
- падающая волна распространяется по направлению нормали к плоскости x0y0;
- точка наблюдения D принадлежит плоскости входной апертуры регистрирующего устройства;
- в приемной плоскости рассматривается лишь конечная область вблизи z, и расстояние z0 много больше максимального размера входной апертуры.
Из последнего следует, что
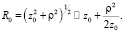(4)
Учитывая данное приближение, а также считая, что объект, рассеивающий излучение, движется равномерно и прямолинейно (без вращений относительно выбранной системы координат x0, y0, z) вдоль оси z со скоростью v так, что
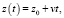(5)
получим окончательную формулу для распределения комплексных амплитуд рассеянного поля на плоскости входной апертуры:
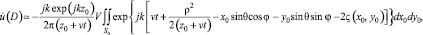
где θ – угол между направлением распространения волны и осью z.
Пусть результирующее распределение комплексных амплитуд поля на плоскости входной апертуры создается за счет совместного воздействия рассеянного поля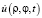 
и поля опорного сигнала. Сигнал когерентного опорного генератора с плоским фазовым фронтом и комплексной амплитудой 
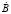на входной апертуре имеет вид
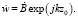(6)
Тогда результирующая интенсивность поля в точке D поверхности входной апертуры имеет вид
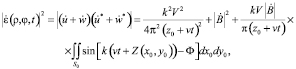(7)
где
,
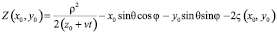а Φ – фазовый угол опорного сигнала, распределение которого по поверхности входной апертуры считаем величиной постоянной.
Если входная апертура имеет форму круга с радиусом ρ0, то сигнал (2) на выходе квадратичного приемника запишется в виде
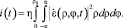(8)
Подставляя (7) в (8) и учитывая здесь и везде далее, что смещение объекта за время измерения невелико по сравнению с расстоянием от объекта до регистрирующего устройства, после тригонометрических преобразований и интегрирования, получим следующее выражение для полного сигнала приемника:
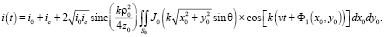(9)
Здесь:
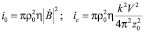(10)
постоянные составляющие сигнала, вызванные опорной и сигнальными волнами соответственно, а функция sinc – ненормированный кардинальный синус.
Перейдем к рассмотрению другого случая, когда размеры шероховатого участка достаточно велики или даже бесконечны, а расстояние между рассеивающим излучение объектом и регистрирующим устройством невелико. То есть воспользуемся решением задачи о дифракции во френелевской области. Выражение для флуктуаций поля над поверхностью с пологими неровностями имеет вид [1]:
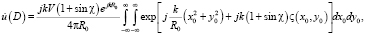
где по-прежнему считаем, что падающая волна распространяется по направлению нормали к плоскости x0y0.
Пусть точка наблюдения D принадлежит плоскости входной апертуры регистрирующего устройства. Используя (4) и (5), получим
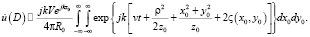(11)
Результатом совместного воздействия рассеянного поля и сигнала (6) когерентного опорного генератора будет распределение интенсивности по поверхности входной апертуры:
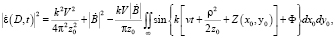(12)
где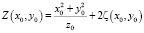 
, v – скорость движения объекта, а Φ – постоянный фазовый сдвиг.
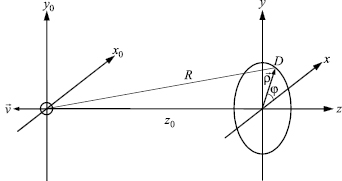
Рис. 2. К исследованию влияния поля, рассеянного движущейся сферической частицей на характеристики сигнала квадратичного приемника
Если, как и в предыдущем случае, входная апертура имеет форму круга с радиусом ρ0 (8), то после необходимых тригонометрических преобразований и интегрирования, и используя обозначения (10), получим следующее выражение для полного сигнала приемника:
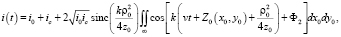(13)
где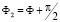 
– постоянный фазовый сдвиг.
Наконец, рассмотрим случай рассеяния излучения движущейся малой частицей сферической формы (рис. 2). Пусть в момент t = 0 в начале системы координат x0y0z0 находится рассеивающая частица.
Известно [4], что комплексная амплитуда поля, рассеянного малой частицей, находящейся в поле плоской оптической волны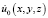 
, может быть записана в виде
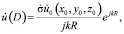
где амплитудная функция рассеяния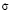 
находится из решения уравнения Максвелла с заданными граничными условиями. Для сферических оптически однородных частиц это решение было дано Ми (G. Mie).
Учитывая (4), (5), (6), получим распределение интенсивности поля по поверхности фотодетектора:
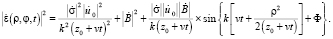(14)
Введя обозначения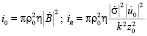 
– постоянные составляющие фототока опорной и сигнальной волн, полный фототок приемника запишется в виде
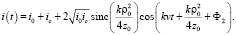(15)
Таким образом, полученные математические модели для всех трех случаев (формулы (7) и (9), (12) и (13), (14) и (15)) позволяют сделать вывод, что полный выходной сигнал доплеровского квадратичного приемника является суммой постоянного сигнала и доплеровской составляющей. Последняя получается в результате воздействия на фотоприемник опорного сигнала и суперпозиции рассеянных движущимся объектом волн. Круговая частота этих волн изменена на величину доплеровского смещения, а статистические характеристики случайной фазы определяются статистическими характеристиками рассеивающей поверхности.
В отличие от метода приема рассеянного излучения с усреднением по спектру пространственных частот (8), в целях использования информации о пространственно-временной структуре рассеянного волнового поля возможно применение пространственно распределенной структуры, регистрирующей излучение с сохранением фазовых характеристик. Последние в связи с движением объекта, рассеивающего излучение, не остаются постоянными во времени. Наличие у регистрирующей структуры интегрирующих во времени свойств позволит производить сравнение принимаемых во время измерения волновых фронтов рассеянного излучения. Результаты сравнения, информация о которых заключена в структуре зарегистрированной интерференционной диаграммы, должны определяться параметрами движения объекта.
Уравнение интерференционной диаграммы, полученной с помощью квадратичной регистрирующей структуры, помещенной в плоскости с полярными координатами ρ, φ имеет вид
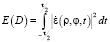, (16)
где τ – время измерения.
Используем полученные выше выражения (7), (12) и (14) для результирующей интенсивности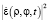 
поля, рассеянного движущимся объектом, в точке D плоскости входной апертуры регистрирующего устройства. Производя интегрирование (16), получим следующие выражения для зарегистрированной интерференционной диаграммы.
Устройство, регистрирующее излучение, рассеянное движущимся объектом со статистически неровной поверхностью, расположено в зоне Фраунгофера:
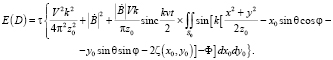(17)
Регистрация излучения, рассеянного движущимся объектом с шероховатой поверхностью, в зоне Френеля:
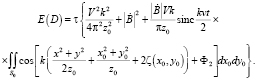(18)
Регистрация излучения, рассеянного движущейся сферической частицей:
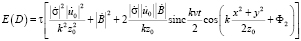. (19)
Анализ полученных выражений для математических моделей зарегистрированной интерференционной диаграммы (17), (18) и (19) позволяет сделать следующие выводы.
Первые два слагаемых во всех трех соотношениях не несут информации о фазовой структуре регистрируемых волновых фронтов рассеянного излучения и не находятся в зависимости от параметров движения объекта. Эти слагаемые определяются лишь интенсивностью рассеянного излучения и интенсивностью опорного сигнала. Третье же слагаемое зависит от фазовых соотношений между элементарными волнами (плоскими или сферическими), приходящими от каждой точки поверхности объекта с координатами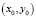 
, и фазовым фронтом опорного сигнала. Кроме того, в отсутствие движения объекта v = 0 и sinc 0 = 1, в результате чего получается интерференционная диаграмма, соответствующая неподвижному объекту. Если v = const по всей площади пространственно распределенной регистрирующей структуры, то контраст интерференционных полос будет слабым для больших значений аргумента функции sinc и нулевым, если аргумент равен 
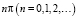. Но так как v неодинакова для всех точек апертуры регистрирующего устройства, контраст полос не нарушается, а скорее пространственно модулируется. Найдя закон пространственной модуляции, можно установить зависимость структуры интерференционной диаграммы от параметров движения объекта.
Надо сказать, что у способов регистрации рассеянного излучения, а именно с усреднением по времени измерения (8) и с усреднением по спектру пространственных частот (16) существуют как принципиальное различие, так и общие свойства.
В случае регистрации с усреднением по спектру пространственных частот (8) получают информацию об изменении во времени фазовых характеристик волнового фронта. Для уменьшения влияния фазовой структуры регистрируемого волнового фронта на результаты измерения стремятся уменьшить область усреднения, что достигается ограничением размеров входной апертуры регистрирующего устройства. В пределе стремятся получить информацию об изменении во времени фазовых характеристик волнового фронта в одной его точке.
Метод сравнения структуры волновых фронтов с применением пространственно распределенной регистрирующей структуры, обладающей интегрирующими во времени свойствами, позволяет использовать информацию об изменении структуры волновых фронтов регистрируемого излучения в континууме точек в течение времени измерения (16). Однако регистрируемая интерференционная диаграмма не должна претерпевать существенных изменений за время измерения, кроме движения полос, что достигается уменьшением времени усреднения.
О наличии указанной корреляции между свойствами пространственных частот в голографической интерферометрии и временными частотами в лазерной анемометрии делается предположение, например, в исследованиях [13, 14].