Основной стратегией в контексте энерго- и массоснабжения является экономия ресурсов материальных потоков [1–3]. В этом случае ведущую роль играет применение современных математических методов [4–6] и использование соответствующей аппаратной поддержки [7].
Типичным примером проявления такой политики является управление системой тепло- и водоснабжения зданий и сооружений. Ведущую роль в упомянутом процессе играет системный подход, позволяющий оптимально обслуживать клиентуру с минимальными расходами генерируемого тепла и подаваемого теплоносителя [8, 9].
В данном случае решение указанной задачи производится по двум направлениям: за счет управления температурой прямого и обратного теплоносителя с учетом температуры наружного воздуха, с одной стороны, и с учетом перехода к более экономичному режиму ночного тепло- и водоснабжения [10].
Соответственно, возникает необходимость в применении точного оборудования и приборов, управляемых различными типами макропроцессоров с применением современных алгоритмов управления [11]. Одним из ведущих параметров, подлежащих особому контролю, является учет удельного расхода теплоносителя в системе теплоснабжения объекта [12].
Подобный подход включает в себя использование приемов дифференциального исчисления при поиске локальных экстремумов некоторой функции цели [13, 14]. В частности, будет произведен поиск ее локального минимума [15] в условиях жестких лимитов снабжения некоторыми исходными средствами производства. В качестве таких средств могут служить вычислительные устройства (ПЭВМ, серверы, контроллеры и т.п.), которые выполняют однотипные вычислительные операции. В условиях грамотной экономии ресурсов такой прием позволяет осуществить научно обоснованный выбор стратегии поиска оптимального значения исследуемой функции.
Главные положения «метода двоек»
Рассмотрим математическую модель, позволяющую оптимизировать распределение материальных потоков среди массива потребителей.
Рассуждение будем вести для объекта исследования (промзоны, города, района, квартала, здания, квартиры и т.п.), содержащего N одинаковых элементарных потребителей какого-либо ресурса.
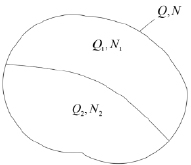
Рис. 1. Условная схема массива потребителей ресурса
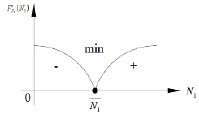
Рис. 2. Локальный минимум функции F(N1)
Предположим, что речь идет о распределении вычислительных средств среди коллективов программистов, если рассматривается возможность оптимального разделения труда в инженерной среде двух, не обязательно равных по количеству работников отделов какого-либо объекта, при написании рабочих программ (алгоритмов).
Пусть данному объекту предоставляется лимит ресурса в объеме не более Q соответствующих единиц. В этом случае плановое (номинальное) число потребителей g на единицу ресурса Q определяется по формуле
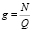 . (1)
. (1)
Произведем распределение упомянутого лимита, применив прием, которому присвоим название – «метод двоек», разбив указанный выше лимит на две условные части (рис. 1), для которых выполняются следующие требования:
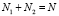 , (2)
, (2)
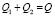 , (3)
, (3)
причем
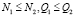 , (4)
, (4)
где N1, N2 – число элементарных потребителей ресурса соответственно в первой и второй частях объекта; Q1, Q2 – минимально необходимые (номинальные) объемы ресурса соответственно для первой и второй частей объекта.
В этом случае соответствующие расходы ресурса для первой и второй частей объекта имеют вид
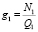 ,
, 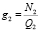 . (5)
. (5)
Рассмотрим функцию F(Q1) одной переменной Q1, учитывая условия (3):
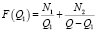 . (6)
. (6)
Исследуем F(Q1) на локальный экстремум. Найдем производную 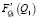 :
:
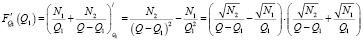 . (7)
. (7)
Определим стационарные точки первого рода по переменным Q1 и Q2:
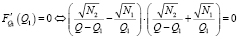 . (8)
. (8)
Так как 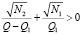 , то имеем
, то имеем
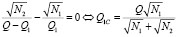 , (9)
, (9)
где ΔQ1C – абсцисса стационарной точки первого рода по переменной Q1.
Из рис. 2 следует, что величина ΔQ1C – абсцисса точки локального минимума.
Учитывая (3), получим
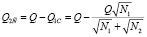 . (10)
. (10)
В этом случае ΔQ2C – абсцисса стационарной точки первого рода по переменной Q2:
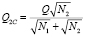 (11)
(11)
Вычислим наименьшее значение функции 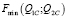 :
:
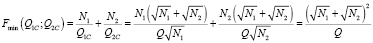 . (12)
. (12)
Диапазон применения «метода двоек»
Рассмотрим динамику изменения запасов ресурса Q в зависимости от варьирования величин N1 и N2 при условии того, что система снабжения функционирует в условиях сбережения ресурсов (9), (11). Проведем исследования, учитывая неравенства (4).
Предположим, что в какой-то момент времени произошло изменение множества N1 потребителей ресурса Q1 на величину ΔN1 ≠ 0.
Одновременно предположим, что другое множество потребителей ресурса N2 изменилось соответственно – на ΔN2 ≠ 0, причем
ΔN1 = – ΔN2, (13)
т.е. число прибывших (убывших) потребителей ресурса Q в множестве N1 переходит в число убывших (прибывших) потребителей ресурса Q в множестве N2 и осуществляется их взаимообмен. В этом случае также происходят соответствующие изменения ресурсов ΔQ1, ΔQ2 и их взаимообмен.
Предварительно свяжем ΔN1, ΔQ1 и соответственно – ΔN2, ΔQ2.
Очевидно, из (9) и (11) следует:
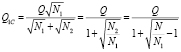 , (14)
, (14)
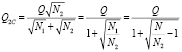 . (15)
. (15)
При наличии обмена в множествах потребителей N1 и N2 соответственно на величины ΔN1 и ΔN2, учитывая (3), (13)–(15), получим соответствующие изменения ресурса ΔQ1C, ΔQ2C в этих множествах:
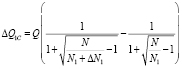 . (16)
. (16)
Полагая, что 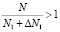 ,
, 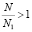 , имеем
, имеем
I) Если 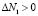 , то
, то
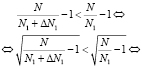
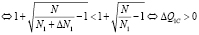 ;
;
II) Если 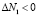 , то
, то 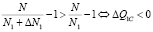 .
.
Аналогично:
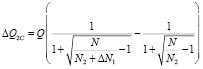 . (17)
. (17)
И в этом случае получим
I) Если 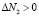 , то
, то 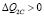 ;
;
II) Если 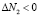 , то
, то 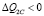 .
.
Сравним приращения ресурсов ΔQ1C и ΔQ2C, используя формулы (9), (11), (13), (16), (17):
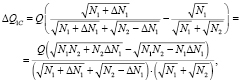 (18)
(18)
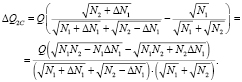 (19)
(19)
Из (18) и (19) имеем
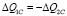 . (20)
. (20)
Следует отметить, что вариант невзаимосвязанного изменения числа потребителей ресурса будет рассмотрен в последующих публикациях.
Замечание. «Метод двоек» можно распространить вглубь для каждой из получившихся частей N1 и N2 массива потребителей N и т.д.
«Метод двоек» может быть расширен до «метода троек», …, «метода n-ок» соответственно для функций цели 3-х, …, n переменных. Это потребует дальнейших исследований и значительно расширит возможности математического анализа в прикладных задачах оптимизации производственных процессов. В этом случае поиск минимума функции n переменных сводится к поиску знака соответствующего дифференциала второго порядка во всех стационарных точках первого порядка данной функции. Легко доказать, что такой экстремум существует всегда.
Важно отметить, что желательно провести исследование по сочетанию методов «двоек», «троек», и т.д. при решении практических задач распределения ресурсов и минимизации материальных затрат. В частности, возможен вариант решения данной задачи в режиме реального времени по факту завершения этапов работ отдельными группами исполнителей.
Предлагаемая методика распределения материальных ресурсов может быть использована при обслуживании крупных жилых и промышленных массивов городской застройки.
Упомянутый алгоритм разбиения вещественных потоков дает возможность автоматизировать энерго- и массосбережение в так называемых «умных домах». В этом случае неизбежно широкое применение управляющих микропроцессоров различного типа, пользующих вышеуказанные ритмы и приемы оптимизации.
Данный подход позволяет обслуживать массивы потребителей с учетом их иерархии и ранжирования на уровне административной классификации объектов снабжения. Не последнюю роль в применении указанного метода играют альтернативные источники энергии, которые можно свести в отдельные группы поставщиков.
«Метод двоек» позволяет решить ряд экономических и финансовых задач при распределении денежных потоков в среде обслуживаемой клиентуры. Здесь возможен подход в планировании и реализации банковских операций в вопросах распределения материальных ценностей.
Данный прием можно также применять в сельском хозяйстве, системе ЖКХ и т.д. Важно отметить, что алгоритм метода оперативно реагирует на изменение исходных показателей.
Выводы
1. Сформулирован подход по разделению структуры обслуживаемого объекта на две части «методом двоек», который представляет величину суммы отношений числа потребителей к соответствующим расходам ресурса по этим частям в виде функции двух переменных от Q1 и Q2.
2. Выполнено исследование полученной функции на локальный экстремум в найденной точке минимума.
3. Получены рабочие формулы распределения лимита ресурсов на две части Q1 и Q2, соответствующие предлагаемым значениям N1 и N2 общего объема N потребителей ресурса на исследуемом объекте.



