Рассмотрим двумерную модель, а именно: рынок с двумя видами активов. Задача участника рынка построена на основе известной модели Марковица [1–3], но отличается от нее тем, что в модель введены дополнительно соотношения, отражающие реальные условия фондового рынка. Это позволяет инвестору определить именно ту структуру оптимального портфеля, которую он реально может создать [2–5]. Для того чтобы сформировать портфель с определенным уровнем доходности и минимальным уровнем риска, инвестору необходимо решить следующую оптимизационную задачу:
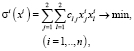(1)
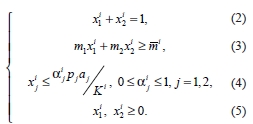
В задаче (1)–(5) верхние индексы показывают принадлежность данного параметра к инвестору, а нижние – принадлежность к виду ценной бумаги;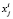 
– доля бумаги вида j в портфеле инвестора i; целевая функция 
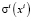инвестора i имеет смысл риска портфеля; clj – коэффициент корреляции между изменениями курсов ценных бумаг вида l и j; mj – ожидаемое значение доходности по бумаге вида j; 
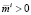– фиксированный уровень доходности, который, как минимум, рассчитывает получить инвестор i; pj – рыночная цена бумаги вида j; aj – количество бумаг вида j на рынке; Ki – инвестиционный фонд инвестора.
Равенство (2) называется основным ограничением. Неравенство (3) отражает тот факт, что для инвестора приемлемы портфели с доходностями не ниже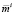 
, т.е. число 
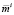задает нижнюю границу ожидаемой доходности. Неравенства (4) отражают тот факт, что инвестор не может приобрести ценной бумаги одного вида больше, чем ее имеется на рынке. Коэффициент 
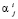позволяет учитывать верхнюю границу инвестирования для каждого инвестора i, т.е. в силу законодательных ограничений невозможно совершать операции купли-продажи объемом более некоторого порогового значения [5–7]. Условия (5) называются условиями неотрицательности.
Любой вектор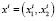 
, удовлетворяющий условиям (1)–(5), будем называть допустимым портфелем инвестора i.
Рассмотрим множество допустимых портфелей инвестора i, удовлетворяющих условиям (2)–(5). Это множество образовано пересечением одной прямой (2) и пяти полуплоскостей (3)–(5), оно зависит от десяти параметров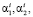 
m1, m2, p1, p2, a1, a2, Ki, 
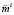. Первые восемь параметров являются сугубо рыночными в том смысле, что находятся, вообще говоря, вне сферы влияния инвестора. Параметры 
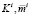устанавливает сам инвестор [7]. Условия (2) и (5) не зависят явным образом от значений 
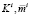, поэтому множество
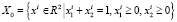(6)
является инвариантным, относительно инвестора, множеством.
Для удобства в будущем введем также множества
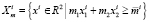, (7)
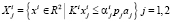. (8)
Теперь можно написать, что допустимое множество (6)–(8) инвестора i есть пересечение множеств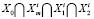 
.
Цель исследования
Исходя из сказанного выше, практический интерес представляет изучение зависимости множества (6)–(8) от размера выделяемого им инвестиционного фонда Ki и его ожиданий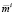 
по поводу доходности портфеля xi. В этом смысле возможности инвестора i можно трактовать так, что, выбирая различные значения Ki и 
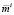, инвестор регулирует положение множеств 
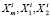относительно «неподвижного» множества X0, сужая или расширяя тем самым множество допустимых портфелей.
Нас, в частности, интересует вопрос: каковым является реальное значение Ki (значение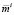 
) для фиксированного 
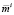(Ki), для которого допустимое множество не пусто, и как оно выглядит.
Отношение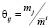 
характеризует долю доходности ценной бумаги вида j в субъективной оценке общей доходности инвестора i.
Выделим два тривиальных случая, относящихся к ограничению (3).
Лемма 1. Если
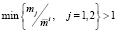, (9)
то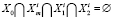 
.
Если
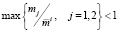, (10)
то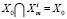 
.
Условие (9) говорит о том, что инвестор ставит перед собой нереальную задачу относительно уровня ожидаемой доходности. Условие (10) означает недооценку уровня доходности.
Условия (9) и (10) являются взаимно исключающими. Так как эти условия заведомо неприемлемы для инвестора, то их можно исключить из дальнейшего рассмотрения, тогда относительно величин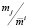 
и ограничения (3) остаются два взаимоисключающих друг друга случая:
1) 
;
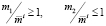2) 
.
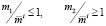Покажем, что эти четыре неравенства по существу являются строгими. Действительно, в случае 1) можно записать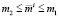 
. Если 
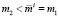, то из (3) имеем 
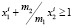, а это, так как 
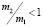, противоречит условию (2). По этой же причине невозможен вариант 
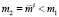. Если 
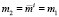, то (3) сводится к (2), поэтому в случае 1) на самом деле 
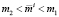. Подобным образом, анализируя случай 2), приходим к строгим неравенствам 
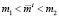. Поэтому вместо 1) и 2) впредь будем рассматривать случаи:
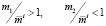, (11)
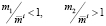. (12)
Рассмотрим сначала случай (11). Справедливы следующие утверждения.
Лемма 2. Пусть выполнено условие (11). Если
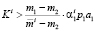, (13)
то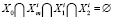 
; если
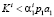, (14)
то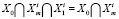 
.
Условия (13) и (14) отражают неоправданно большой и маленький объемы инвестиционного фонда инвестора i. Мы их также исключаем из дальнейшего рассмотрения.
Условия (13) и (14) относятся к первому из ограничений (4). При условиях (11) и (12) неравенство (4) описывает открытую полуплоскость, расположенную левее прямой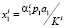 
, которая проходит левее точки пересечения
,
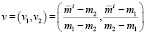границы множества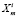 
с отрезком X0. При условиях (11) и (12) неравенство (4) описывает открытую полуплоскость, расположенную левее прямой 
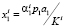, когда она пересекает ось 
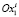левее точки (1,0). Здесь имеется в виду изменение положения прямой 
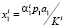при различных значениях Ki.
Нетрудно заметить, что после исключения неприемлемых условий (13) и (14), в обсуждаемом нами случае (11) относительно первого из ограничений (4) остается единственный приемлемый вариант
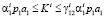, (15)
где
.
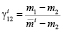Из (15) получаем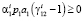 
или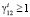 
, а это означает, что 
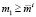. С другой стороны, с учетом (11) из вида 
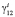получаем 
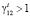. Для совместимости с условием (11) в (15) принимаем 
.
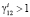Рассмотрим точку
,
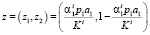пересечения границы множества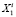 
с отрезком X0.
Ввиду взаимоисключаемости условий (13), (14) и (15), в случае нарушения неравенства (15) мы оказываемся либо в условиях (13), либо в условиях (14) (см. лемму 2), поэтому уместно следующее утверждение.
Лемма 3. Пусть выполнено условие (11). Тогда размер инвестиционного фонда Ki должен удовлетворять условию (15) и в этом случае
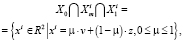(16)
где μ параметр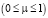 
.
Приведенное в лемме 3 множество (16), соответствующее условию (15), шире множества допустимых портфелей, так как оно получено без учета второго из ограничений (4).
Обозначим
.
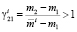Лемма 4. Пусть выполнены условия (11) и (15). Если при этом
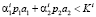, (17)
то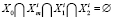 
; если
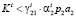, (18)
то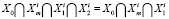 
.
Условия (17) и (18) относятся ко второму из ограничений (4) и допускают аналогичную с условиями (13) и (14) трактовку, поэтому мы их исключаем из дальнейшего рассмотрения. Геометрические рассуждения по поводу условий (17) и (18) приводят к следующему аналогу условия (15) относительно второго из ограничений (4):
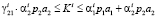. (19)
Можно показать, что это условие совместимо с условиями (11) и (15).
Обозначим через
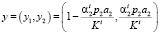
точку пересечения границы множества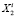 
с отрезком X0.
Ввиду взаимоисключаемости условий (17), (18) и (19), в случае нарушения неравенства (19) мы оказываемся либо в условиях (17), либо в условиях (18) (см. лемму 4), поэтому уместно следующее утверждение.
Лемма 5. Пусть выполнены условия (11) и (15). Тогда размер инвестиционного фонда Ki должен удовлетворять условию (19) и в этом случае
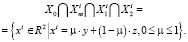
Объединяя леммы 1–5 воедино, приходим к следующему результату.
Основные результаты
Теорема 1. Если в задаче (1)–(5) инвестор определяет ожидаемый уровень доходности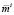 
из условия 
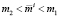, то объём его инвестиционного фонда Ki должен удовлетворять условию
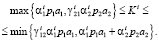(20)
В этом случае множество допустимых портфелей не пусто и имеет вид
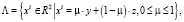(21)
где
,
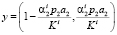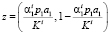. (22)
Рассматривая теперь случай (12) и рассуждая аналогично, приходим к следующему результату.
Теорема 2. Если в задаче (1)–(5) инвестор определяет ожидаемый уровень доходности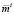 
из условия 
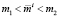, то объём его инвестиционного фонда Ki должен удовлетворять условию
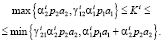(23)
В этом случае множество допустимых портфелей не пусто и имеет вид (21), где векторы y и z по виду такие же, что и в (22).
Отметим еще раз, что относительно величины θij могут иметь место четыре взаимоисключающих друг друга случая (9)–(12). Случаи (9) и (10) назовем тривиальными. Объединяя теоремы, приходим к окончательному результату.
Теорема 3. В задаче (1)–(5), за исключением тривиальных случаев, имеет место один из двух вариантов определения уровня ожидаемой доходности инвестора i:
1) 
,
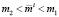2) 
.
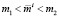В первом случае инвестиционный фонд должен быть выбран из условия (20), а во втором случае – из условия (23). В обоих случаях множество допустимых портфелей не пусто и имеет вид (21).
Заключение
Как показывают проведенные исследования, любой допустимый портфель можно получить как выпуклую комбинацию крайних портфелей y и z. Если ожидания инвестора i удовлетворяют условию (11), то, подставляя в основное ограничение выражения
,
,
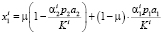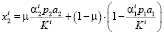мы определим новую целевую функцию:
,
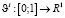так что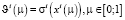 
.
Таким образом задача (1)–(5) сводится к следующей простой задаче математического программирования:
,
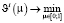для решения которой существуют хорошо известные алгоритмы [8].