Мониторинг состояния сложного объекта или процесса необходим для раннего выявления опасных ситуаций или их устранения с незначительными потерями. Исходной информацией для мониторинга служат данные, снимаемые с датчиков, которые характеризуют изменения параметров отслеживаемого объекта. На основе этой информации возможно прогнозирование отдельных параметров объекта. В этом случае, при условии реализации этого процесса в реальном времени возможна оценка состояния объекта на последующие временные промежутки, следующие за текущим. Таким образом, вопросы прогнозирования параметров являются актуальными для обеспечения безопасности функционирования сложных объектов и процессов [1–3].
Развитие цифровой техники, внедрение различных микроконтроллерных систем в составе систем мониторинга сложных объектов делает эту задачу реализуемой. Расчеты, выполняемые в микроконтроллерных системах в режиме реального времени, обеспечивают быстрое реагирование на изменяющуюся ситуацию. Для прогнозирования параметров объекта целесообразно использовать простые вычислительные, поскольку их можно реализовать в микроконтроллере в фоновом режиме. Такой дополнительный алгоритм не должен существенно менять нагрузку на микроконтроллер. В качестве простых моделей предлагается взять модели временных рядов [4, 5].
Постановка задачи
В работе рассматривается алгоритм прогнозирования параметра объекта с использованием модели многократного экспоненциального сглаживания его временного ряда. Оценка возможности и качества прогнозирования определяется на основе обработки данных, снимаемых с датчика ускорения. В качестве датчика взят автомобильный акселерометр. Съем данных об ускорении осуществлялся при движении автомобиля в различных дорожных условиях.
Схема прогнозирования разрабатывалась на основе модели многократного экспоненциального сглаживания. Предполагалось, что интервал дискретизации будет небольшим, его можно зафиксировать так, чтобы изменение параметра на протяжении нескольких интервалов оставалось незначительным, в среднем рост или падение значения параметра не более 10–15 %. Это снизит погрешность прогнозирования.
Положим, что измерения параметра объекта или процесса y(t) фиксируются с помощью акселерометра и записываются в память микроконтроллера. Интервал фиксации измерений равен h. Таким образом, имеется вектор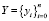 
. Элементами вектора являются значения параметра 
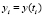, которые фиксированы в точках 
; 
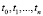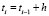. Задача заключается в вычислении значений y в точках T + kh, k = 1, K. Здесь T – текущее значение времени. Число k определяет глубину прогнозирования.
Результаты моделирования
Исходным является временной ряд в виде полинома первой степени [1, 4]:
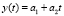. (1)
Значение параметра в T + τ определяется согласно выражению
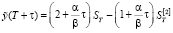. (2)
Величины ST и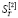 
вычисляются по формулам
, 
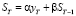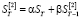. (3)
В предыдущем выражении величина α – постоянная сглаживания, β = 1 – α. Постоянная α влияет на способность временного ряда сглаживать измеренные значения параметра и тем самым влияет на процесс прогнозирования.
Величины S0 и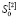 
определяются в начале процедуры прогнозирования:
, 
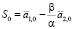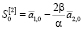. (4)
Коэффициенты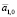 
и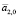 
представляют собой предварительные значения величин a1 и a2 в (1). Их можно определить различными способами, но обычно используется метод наименьших квадратов.
Как было ранее сказано, в качестве исходных данных использовались данные об ускорении, снимаемые с соответствующего датчика ускорений. Полученная функция является знакопеременной, разброс значений достаточно большой, временной интервал между значениями составляет h = 0,015625 сек.
Для прогнозирования параметра необходимо определить несколько коэффициентов, которые влияют на процесс. Коэффициенты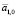 
и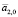 
определяются на известном участке временного ряда таким образом, чтобы формируемая ими функция (1) определяла тренд временного ряда на выбранном временном интервале. Правильный выбор этих коэффициентов способствует быстрому выходу в режим прогнозирования и устранению или существенному сокращению временного интервала, на котором временной ряд подстраивается под динамику снимаемых экспериментальных данных [6]. За пределами этого временного интервала коэффициенты 
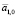и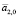 
не влияют на погрешность прогнозирования. Этого нельзя сказать в отношении коэффициента α. Правильный выбор этого коэффициента напрямую влияет на характер процесса прогнозирования и определяет величину погрешности.
Прогноз поведения отслеживаемого параметра с использованием модели временного ряда при различных величинах коэффициента α показан на рис. 1. Временной интервал, на который осуществляется прогнозирование, равен h.
Коэффициент α может изменяться от 0 до 1. Его увеличение приводит к большей чувствительности временного ряда, формируемого в процессе моделирования. Он более точно воспроизводит экспериментальную кривой. Но в то же время снижаются сглаживающие возможности временного ряда, что приводит к увеличению чувствительности ряда к отдельным выбросам, увеличивая тем самым погрешность прогнозирования. Очевидно, что для повышения эффективности прогнозирования необходима настройка ряда, заключающаяся в выборе коэффициента α, соответствующего текущей зависимости, полученной в результате измерения параметра [4]. Рис. 2 иллюстрирует эту особенность временного ряда.
Из анализа графиков следует, что в случае быстрого увеличения параметра более низкую погрешность дает использование ряда с высоким значением коэффициента α. Если же наблюдается медленный рост или небольшие колебания, то целесообразно использование временного ряда со значением коэффициента α, близким к нулевому. Поскольку усложнение алгоритма подбора и установки α в условиях реализации алгоритма в фоновом режиме недопустимо, должно быть выбрано одно значение этого коэффициента и так, чтобы процесс прогнозирования был сбалансирован с точки зрения достаточности погрешности для решения задачи отслеживания и предотвращения нештатных ситуаций. Общие положения по выбору коэффициента приведены в [4, 6]. На основе предварительного моделирования с учетом указанных в [4, 6] общих положений для контролируемого параметра был выбран коэффициент α, равный 0,35. На рис. 3 представлены результаты моделирования с использованием временного ряда с α = 0,35 в случае различных временных интервалов прогнозирования.
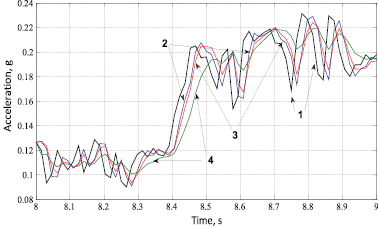
Рис. 1. Прогноз поведения параметра с использованием модели временного ряда: 1 – зависимость параметра от времени; 2 – прогноз при α = 0,55; 3 – прогноз при α = 0,35; 4 – прогноз при α = 0,15
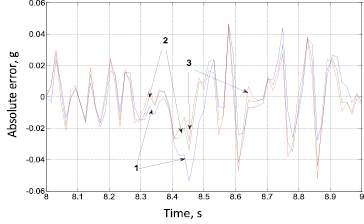
Рис. 2. Погрешность прогнозирования: 1 – α = 0,15; 2 – α = 0,35; 3 – α = 0,55
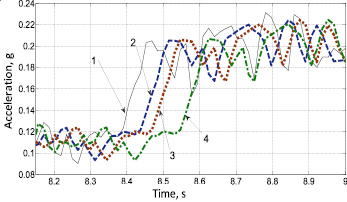
Рис. 3. Прогноз поведения параметра при α = 0,35: 1 – зависимость параметра от времени; 2 – прогноз при τ = 3h; 3 – при τ = 5h; 4 – при τ = 10h
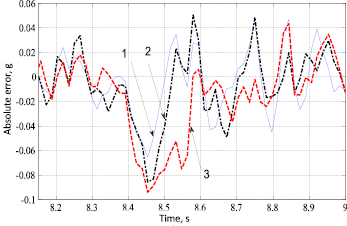
Рис. 4. Погрешность прогнозирования при α = 0,35: 1 – интервал прогнозирования τ = 3h; 2 – интервал прогнозирования τ = 5h; 3 – интервал прогнозирования τ = 10h
Если сравнивать погрешности прогноза для различных интервалов прогнозирования, то наименьшая погрешность соответствует наименьшему из представленных интервалов (рис. 4).
Представленные результаты показывают, что выбранную модель временного ряда целесообразно использовать для краткосрочного прогнозирования параметра, поскольку при больших интервалах прогнозирования, более 5h, время запаздывания прогноза в среднем сравнимо с величиной этого интервала. Это существенно увеличивает погрешность прогноза.
Схема реализации процесса прогнозирования
1. На первом этапе с использованием (1) вычисляются значения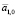 
и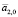 
. Это оценки коэффициентов a1 и a2. Определить эти значения можно методом наименьших квадратов, используя в качестве исходных данных значения параметра, снятые с датчика ускорений на начальном этапе моделирования.
2. Начальное значение коэффициента α можно установить в диапазоне [0,1…0,3], как рекомендовано в [7]. Эта величина корректируется в процессе настройки ряда. В качестве исходных данных используются ранее полученные значения параметра. Критерием является снижение погрешности прогнозирования до уровня, приемлемого для конкретного случая применения модели. В процессе настройки следует учитывать, что увеличение α приводит к уменьшению среднего возраста используемой информации и наоборот [4]. Средний возраст информации определяется по соотношению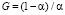 
. Для краткосрочного прогнозирования необходим баланс влияния более старых по времени и новых данных.
3. На следующем этапе подготовки модели для проведения процесса прогнозирования с учетом соотношений (4) вычисляются значения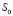 
и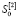 
. Определяется интервал прогнозирования, например τ = h.
4. Прогнозирование выполняется для каждой временной точки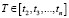 
на интервал прогнозирования τ, т.е. определяется возможное значение параметра в точке T + τ. Для каждой точки T вычисляются экспоненциальные средние ST и 
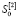согласно выражению (3). Затем согласно (2) вычисляется прогнозное значение параметра 
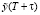в точке T + τ. Следует отметить, что в самом начале моделирования прогнозирующая и прогнозируемая кривые могут сильно отличаться по форме и значениям. Это связано с наличием периода настройки модели. Его длительность напрямую зависит от правильности определения значени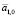й 
и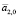 
. Завершение периода настройки можно определить по факту приближения прогнозирующей кривой к экспериментальной. Далее прогнозирующая кривая в целом повторяет форму экспериментальной с некоторым запаздыванием.
5. Для снижения погрешности прогнозирования возможно использование различных коэффициентов α для участков изменения параметра с разной динамикой. Увеличение коэффициента уменьшает средний возраст информации, используемой для прогнозирования и, следовательно, снижает погрешность прогнозирования для быстро меняющихся участков изменения параметра. Соответственно, для менее динамичных участков изменения параметра коэффициент ? целесообразно снизить.
Заключение
В статье рассмотрены особенности процесса прогнозирования параметра сложного объекта с использованием модели временного ряда, основанного на многократном экспоненциальном сглаживании результатов измерения параметра. Проведена качественная оценка влияния коэффициентов настройки временного ряда для решения задачи прогнозирования. Показано, что для устранения или значительного сокращения периода настройки ряда необходимо достаточно точно задать начальные коэффициенты аппроксимации экспериментальной зависимости. Целесообразно использовать для вычислений метод наименьших квадратов.
Предложена схема реализации процесса прогнозирования, разбивающая процесс на этап настройки и этап прогнозирования. Определены схема и правила подбора коэффициента сглаживания временного ряда в зависимости от скорости изменения прогнозируемого параметра. Предложенная модель прогнозирования направлена на ее выполнение в микроконтроллере системы мониторинга объекта в фоновом режиме, без существенного снижения производительности и загрузки.
Полученные результаты могут быть использованы в системах мониторинга и контроля различных объектов и процессов для предупреждения развития нештатных и аварийных ситуаций.