Необходимость данного исследования возникла из многолетнего опыта эксплуатации амфибийных транспортных машин с аэродинамическими движителями (далее – амфибийных машин), разрабатываемых Поволжским государственным технологическим университетом по заказам ряда предприятий нефтегазовой промышленности, энергетики, рыбного хозяйства.
Эксплуатация таких машин в условиях Северного Каспия при движении по торосистому льду, битому льду с водой, при выходе из воды на лед показала, что первоначальные признаки разрушения валов воздушных винтов обнаруживаются на значительно более ранних стадиях эксплуатации, чем это происходит в более благоприятных условиях.
Это обстоятельство вызывает необходимость более полного и точного учета всех видов нагрузок, действующих на амфибийную машину при ее движении по пересеченной местности, в том числе гироскопических моментов. Данная статья продолжает цикл работ авторов [1–3] в этом направлении.
Цель исследования
Одной из целей работы является привлечение внимания специалистов, занимающихся созданием амфибийных машин (аэроботов, аэроглиссеров), к проблеме обеспечения надежности наиболее ответственных деталей, например валов воздушных винтов. Это обстоятельство придает работе повышенную актуальность.
Вал воздушного винта в условиях эксплуатации испытывает сложное напряженное состояние, определяемое воздействием изгибающих и вращающих моментов. Основными силовыми факторами, вызывающими в теле вала напряжение изгиба, являются гироскопические силы и сила тяжести винта. При этом наиболее сложной задачей является учет влияния гироскопического момента на усталостную прочность вала винта.
Материалы и методы исследования
В связи с тем, что возникновение гироскопического момента носит случайный характер и зависит от множества факторов, в основу расчета и оценки его влияния на долговечность вала должны быть положены вероятностные методы.
Известные методы расчета усталостной прочности, содержащие вероятностный подход, предполагают использование нормального закона распределения случайных параметров. Этот закон может быть реализован применительно к изучению усталостной прочности вала воздушного винта амфибийной машины.
Напряжения от действия гироскопического момента прямо пропорциональны его значению. Величина гироскопического момента определяется выражением [3]:
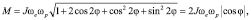(1)
где J – осевой момент инерции винта; ωe – угловая скорость винта; ωp – угловая скорость движущейся амфибийной машины; φ – угол поворота винта в принятой системе отсчета.
Параметры J и ωe могут считаться постоянными, а ωp и φ имеют случайные значения и зависят от факторов, среди которых главными являются: характер неровностей профиля пути, искривление пути в плане, профиль скользящей поверхности амфибийной машины, скорость движения.
Из названных факторов при исследовании движения амфибийной машины конкретной конструктивной схемы выделим характер неровностей профиля пути, предполагая, что движение происходит с постоянной скоростью (возможность варьирования значением скорости при этом не исключается). Повороты амфибийной машины в плане будем рассматривать в дальнейшем как разовые явления.
Обратимся к известным данным о микропрофиле бездорожья, представленным в виде расчетных корреляционных функций [4, 5]. Максимальная высота неровностей h, соответствующая конкретному типу бездорожья, выражена формулой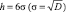 
, где σ – среднеквадратичное отклонение, D – дисперсия случайного процесса изменений высот неровностей. Значения h (высота неровности) и l (длина основания неровности) для различных типов бездорожья приведены в таблице.
Используя данные (таблица) и предполагая, что характер неровностей подчиняется нормальному закону распределения, можно определить математическое ожидание по правилу «трех сигма» и среднеквадратичное отклонение высот для конкретного типа неровностей. Например, для неровности типа «возвышенность» среднеквадратичное отклонение равно 8 см, а математическое ожидание hm = 25 см. К этому типу относятся высохшие болота средней полосы, возвышенности полупустыни и тундры [4, 5]. Высота их неровностей составляет до 50 см. Отсюда следует, что кривая плотности вероятностей в данном случае имеет вид представленный на рис. 1.
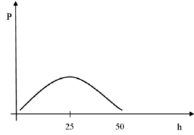
Рис. 1. Кривая плотности вероятностей
Отметим, что корреляционные функции [5], получены в результате обработки экспериментальных данных методом пересечений, принимая за случайную величину только отклонение микропрофиля от условной горизонтальной плоскости. Поэтому действительное математическое ожидание равно нулю.
Чтобы не оперировать с отрицательными высотами, условная горизонтальная плоскость была опущена на 25 см и получено hm = 25 см.
Напряжение изгиба вала σв от действия гироскопического момента определяется по формуле
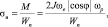(2)
где Wn – осевой момент сопротивления изгибу. Зависимость напряжения от ωp является линейной.
Истинно утверждение [6, 7]: «Линейная функция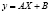 
нормально распределенного аргумента X также распределена нормально, причем для того, чтобы найти математическое ожидание y, надо в выражении функции подставить вместо аргумента X его математическое ожидание a: 
».
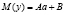Значения h (высота неровности) и l (длина основания неровности) для различных типов бездорожья
|
Параметры |
Все виды лугов |
Валы |
Возвышенности |
Укатанная дорога |
Разбитая дорога |
|
Высота неровности h, м |
0,3 1,4 |
1,2 1,62 |
0,5 |
0,14 0,25 |
0,36 0,6 |
|
Длина основания неровности l, м |
15 30 |
20 30 |
0,6 |
4,5 19 |
8 30 |
Следовательно, изменение напряжения в вале происходит по нормальному закону, а его математическое ожидание находится по формуле
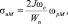(3)
где σвМ – математическое ожидание напряжения в вале;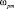 
– математическое ожидание угловой скорости ωp. Множитель 
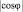принимается равным единице.
Среднеквадратичное отклонение процесса изменения напряжений в вале находится по формуле
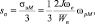(4)
где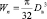 
, где Dв – диаметр вала.
Тогда по утверждению [8] и пояснению [9] можно считать, что закон распределения амплитуд напряжений случайного процесса изменений напряжений в вале винта является релеевским со среднеквадратичным отклонением (4).
Формула (1) позволяет найти наибольшее значение угловой скорости ωp, которую приобретает амфибийная машина при преодолении за время t вершины препятствия высотой h (рис. 2). За это время воздушный винт сделает ωet оборотов. При этом произойдет ωet циклов нагружения вала. Максимальное напряжение циклов достигает значения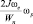 
.
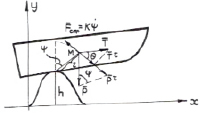
Рис. 2. Вращение амфибийной машины при преодолении препятствия
Вращение при преодолении вершины препятствия происходит по часовой стрелке при падении носовой части с одновременным скольжением днища по верхней части препятствия до удара передней части днища о землю.
В этом вращении амфибийная машина поворачивается на угол
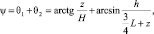(5)
где H – расстояние от центра тяжести т. M до днища, L – длина днища, z – расстояние между проекцией т. M и верхней точкой h.
При этом вращении ускорение, направленное по касательной к траектории движения т. M, создается составляющей рτ силы тяжести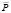 
, составляющей силы тяги 
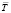и силами сопротивления 
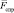, оказываемыми движению воздухом и вершиной препятствия.
Последние весьма сложным образом зависят от происходящего вращения, от структуры вершины препятствия и его формы. Существенно упрощая имеющуюся сложную зависимость, будем считать, что эти силы создают результирующую, пропорциональную угловой скорости 
и направленную по касательной к траектории движения центра масс. Тогда векторное уравнение, связывающее ускорение 
, направленное по касательной к траектории движения, будет следующим:
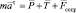. (6)
Это уравнение в координатной форме примет вид
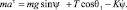(7)
Воспользуемся равенством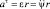 
и введем обозначения:
, 
,
, (
).
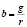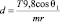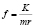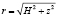Подставив введенные обозначения в уравнение (7), будем иметь
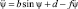. (8)
Воспользовавшись равенством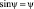 
(для малых углов), можно из уравнения (8) получить уравнение, которое даст решение, близкое к истинному:
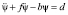. (9)
Нахождение его общего решения не представляет трудности. Начальные условия для получения частного решения очевидны (при t = 0,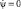 
и ψ = 0).
Результаты исследования и их обсуждение
Формула (1) позволяет найти наибольшее значение угловой скорости ωp, которую приобретает амфибийная машина при преодолении вершины препятствия высотой h. За время t воздушный винт сделает ωet оборотов. При этом произойдет ωet циклов нагружения вала. Максимальное напряжение циклов достигает значения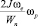 
.
Срок службы вала воздушного винта, выражаемого количеством преодоленных препятствий, вычисляется по формулам
а) для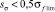 
:
; (10)
б)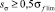 
:
где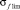 
– предел выносливости при изгибе, Tn – ресурс вала, выраженный в секундах, Te – «эффективный период», ωe – угловая скорость винта, tкрит. – время вращения амфибийной машины при преодолении вершины препятствия, когда ускорение направлено по касательной к траектории движения, N0, m1 – эмпирические константы:
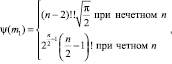
где
,
;
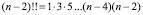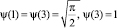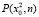– значение интеграла вероятности x2:
.
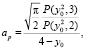
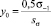Для нахождения t3крит. решается дифференциальное уравнение (8), используя начальные условия t = 0,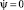 
и ψ = 0, получим решение в преобразованном виде:
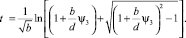(11)
Для того чтобы найти tкрит., необходимо подставить в (11) значения b, d, ψ, соответствующие hкрит..
Заключение
Результаты исследования были использованы при расчете и конструировании винтомоторных установок амфибийных машин, разрабатываемых в Поволжском государственном технологическом университете. Амфибии «Каспий-2М» и «Каспий-5М» выпускались серийно и эксплуатировались в зимнее время на Северном Каспии в условиях торосистого льда, битого льда с водой и открытой воды.
Длительная производственная эксплуатация амфибийных машин показала требуемую надежность и долговечность валов воздушных винтов, что подтверждает достоверность расчетов.