Задачи математического моделирования течений в восходящих закрученных потоках типа торнадо и тропический циклон при учете действия сил тяжести и Кориолиса рассматривались ранее [1, 2]. В работах [3, 4] рассматривались течения политропного газа в некоторой окрестности свободной поверхности, разделяющей газ и вакуум. Показано, что в случае примыкания газа к вакууму закрутка газа происходит против часовой стрелки в северном полушарии. Более подробная библиография приведена в работе [5]. В [5] рассматривалось течение газа в некоторой окрестности вертикальной контактной характеристики кратности два, разделяющей восходящий закрученный поток и покоящийся газ. В данной работе продолжаются исследования [5] для конической контактной поверхности.
Постановка задачи
Рассматриваются стационарные изэнтропические течения политропного газа со следующими искомыми газодинамическими параметрами: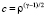 
– скорость звука в газе; u – радиальная составляющая вектора скорости газа; v – тангенциальная составляющая вектора скорости газа; w – вертикальная составляющая вектора скорости газа. Здесь ρ – плотность газа, γ – показатель политропы газа. Газодинамические параметры зависят от независимых переменных: r – полярного радиуса в плоскости xOy; φ – полярного угла; z – третьей пространственной координаты. Значение переменной z отсчитывается от поверхности Земли.
В качестве математической модели, описывающей стационарные конические течения политропного газа, выбирается система газовой динамики, учитывающая воздействие сил тяжести и Кориолиса [6]:
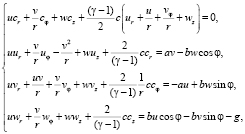(1)
где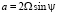 
, 
, 
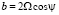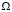– модуль угловой скорости вращения Земли, ψ – широта точки 
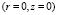на поверхности Земли, g = const > 0 – ускорение свободного падения.
Построение и исследование течения будем проводить в окрестности точки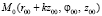 
, r00, φ00, z00 = const > 0, k ≥ 0.
Будем искать конические характеристики этой системы в виде
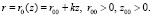
В системе (1) введем новую независимую переменную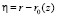 
, не меняя переменных z, φ [3, 7]. При этой замене переменных система (1) переходит в следующую систему:
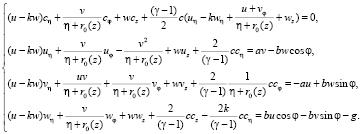(2)
Поставим начально-краевую задачу на характеристике η = 0 кратности 2.
Как и в [5], функция c0 имеет вид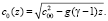 
Сформулируем следующие начальные условия на η = 0:
(3)
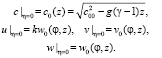(4)
Здесь c00 – константа, при помощи которой задается значение скорости звука покоящегося газа при z = 0,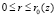 
.
Для получения единственного решения задачи (2), (4) зададим два дополнительных условия
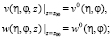(5)
с аналитическими в окрестности точки (η = 0, φ= φ00, z = z00) функциями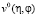 
, 
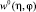, которые удовлетворяют условиям согласования
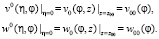(6)
Далее будем предполагать, что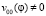 
, 
.
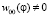Построение аналитического решения задачи (2), (4), (5)
Решение задачи (2), (4), (5) будем строить в виде ряда по степеням η.
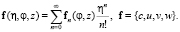(7)
В системе (5) положим η = 0 и при обозначениях
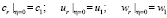
получим следующие четыре соотношения:
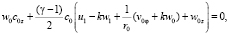
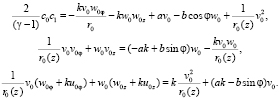(8)
Из первого и второго уравнения системы (8) определяется коэффициент ряда (7) c1 и получается алгебраическое соотношение между коэффициентами u1, w1.
Третье и четвертое уравнения системы (8) являются необходимыми условиями разрешимости характеристической задачи Коши [7]. Поэтому функции v0 и w0, должны удовлетворять этим уравнениям. Из равенства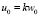 
найдем производные
.
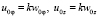Подставляя полученные производные в третье и четвертое уравнение системы (8), получим систему уравнений
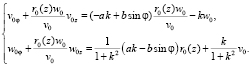(9)
С начальными условиями, полученными из условий (6),
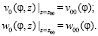(10)
Так же как и в [3, 5], по методике, описанной в [8], перейдем от системы с частными производными (9) к системе обыкновенных дифференциальных уравнений. Здесь τ – характеристический параметр.
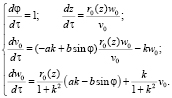(11)
Для системы (11) получаются следующие начальные условия
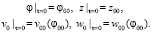(12)
Умножим третье уравнение системы (11) на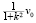 
, а четвертое уравнение на w0 и, складывая их, получим следующее дифференциальное уравнение
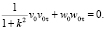(13)
Уравнение (13) имеет общее решение, удовлетворяющее следующему равенству:
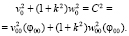(14)
Следовательно, на контактной поверхности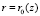 
вдоль бихарактеристики системы (2) для конических течений, как и в [5], имеет место
Закон сохранения. Если уменьшается (увеличивается) модуль вертикальной составляющей вектора скорости газа, то увеличивается (уменьшается) модуль тангенсальной составляющей вектора скорости газа в соответствии с формулой (14).
Интегрируя второе уравнение системы (11), имеем
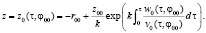
В отличие от [5] третье и четвертое уравнение системы (11) проинтегрировать не удалось. Тем не менее задача (11), (12) имеет единственное аналитическое решение и далее будем считать известными функции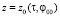 
, 
, 
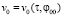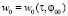и, следовательно, 
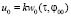– нулевые коэффициенты ряда (7).
Дифференцируя систему (2) n раз по η и положив η = 0, после преобразований будем иметь
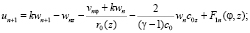
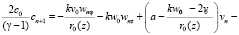
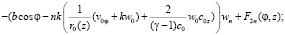
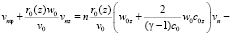
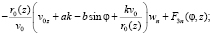(15)
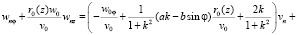
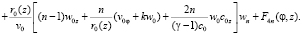
Здесь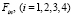 
– функции, известным образом зависящие от ранее найденных коэффициентов ряда (7).
Вводя в третьем и четвертом уравнении системы (15) характеристический параметр τ, получим
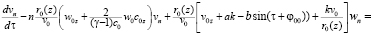
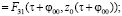
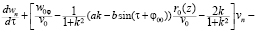(16)
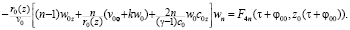
Соотношения на бихарактеристике сохраняются в виде
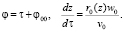
Начальные условия для систем (16) получаются из условий (5), если функции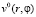 
, 
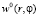разложить в ряд по степеням r – r00.
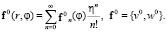(17)
В параметрической форме начальные данные имеют вид
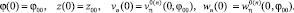(18)
Таким образом, в виде рядов (7) построено единственное локально аналитическое решение задачи (2), (4), (5).
Численное моделирование течения газа на вертикальной контактной поверхности и в ее окрестности
Для построения цилиндрических течений газа возьмем k = 0, тогда контактная поверхность будет иметь уравнение r = r00 – цилиндр [5]. В этом случае удалось проинтегрировать третье и четвертое уравнения системы (11). Получены следующие формулы [5]:
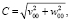
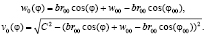
Расчеты газодинамических параметров и траекторий проводились по этим формулам и уравнениям для бихарактеристик
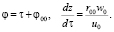
Для расчетов использовались следующие безразмерные величины:
γ = 1,4, b = 0,001379, r00 = 1, z00 = 0,00027, c00 = 1, v00 = 0,159, w00 = 0,0024.
При введении безразмерных переменных в качестве масштабов скорости и расстояния брались соответственно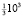 
м/с и 3650 м. Использование таких входных данных соответствует тропическому циклону средней интенсивности, находящемуся на широте 
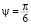[1]. В восходящем закрученном потоке с приведенными значениями входных констант частица газа, сделав полный оборот по поверхности цилиндрической контактной поверхности с размерным значением ее радиуса r00 = 3650 м, поднялась на высоту 3462 м.
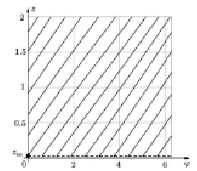
Рис. 1. Бихарактеристики z = z0(τ, φ00)
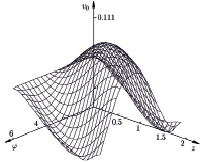
Рис. 2. Интегральная поверхность для функции v0(φ, z)
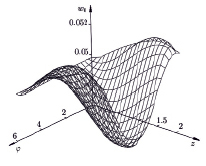
Рис. 3. Интегральная поверхность для функции w0(φ, z)
На рис. 1 приведены бихарактеристики z = z0(τ, φ00), при численном построении которых с шагом Δτ = 0,001 выбирались точки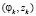 
: фиксировалось φ00, вычислялось 
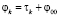и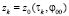 
.
Таким образом, построена неравномерная сетка для переменных φ, z. В узлах этой сетки и вычислялись значения функций v0(φ, z), w0(φ, z).
В результате из бихарактеристик численно построены интегральные поверхности для параметров газа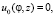 
v0(φ, z), w0(φ, z) на цилиндрическом контактном разрыве. На рис. 2, 3 приведены интегральные поверхности для функций v0(φ, z), w0(φ, z).
Авторы благодарят д.ф.-м.н., профессора С.П. Баутина за полезное обсуждение данной работы.