При анализе экспертных оценок часто возникает проблема их согласованности. Она связана с тем, что эксперт, сравнивая альтернативы попарно, не обязан думать о взаимоотношениях этих альтернатив со всеми остальными. При этом могут возникнуть нарушения транзитивности суждений, которые делают бессмысленной дальнейшую обработку результатов. Вероятность возможных нарушений согласованности повышается с увеличением размерности оценочных матриц. Для решения указанной проблемы предлагается использовать следующий алгоритм.
Пусть в распоряжении исследователя имеется статистическая информация об объектах исследования, функционирование которых оценивается по 
показателям. Сформируем эту информацию в виде матрицы
(1)
где: n - число рассматриваемых объектов исследования; Xij - значение j-того оценочного критерия для i-того объекта.
Для последующего корректного формирования исходных данных для задачи ЛП необходимо привлечение квалифицированного эксперта или группы экспертов. Задача эксперта на первом этапе сводится к определению пар объектов, в которых один функционирует в целом "лучше" по отношению ко второму по выделенному блоку показателей. Или, формально, к определению индексного множества пар:
(2)
для которых 
, 
.
Вместе с тем, могут существовать такие пары объектов результаты функционирования которых, по мнению экспертов, являются примерно одинаковыми. На их основе формируется другое индексное множество - E:
(3)
для которого 
, 
.
Как указывалось выше, основными трудностями парных сравнений являются нарушения транзитивности отношений пар объектов и неполнота экспертных определений, заключающаяся в несоответствии указанных во множествах А и Е объектов исследования к их исходному заданию.
На основе указанных экспертами пар предпочтений и эквивалентности строится вспомогательная матрица Y размерности, 
, по которой осуществляется предварительная оценка результатов экспертизы. Величины 
устанавливают соотношения между объектами и в соответствии с (2 и 3), могут быть определены следующим образом:
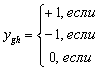
(4)
Очевидна асимметричность пары элементов 
и 
относительно главной диагонали матрицы Y. Поэтому достаточно рассмотрения наддиагональной части указанной матрицы.
Далее, в соответствии с требованиями достижения транзитивности, добавляются новые соотношения между объектами по следующим правилам (5):
5.1. если 
= 0 и 
= -1, то 
= -1;
5.2. если = 1 и = -1, то = -1;
5.3. если = 0 и = 1, то = 1;
5.4. если = -1 и = 1, то = 1;
5.5. если = 1 и = 0, то = -1;
5.6. если = -1 и = 0, то = 1;
5.7. если = 0 и = 0, то = 0;
5.8. если = -1 и = -1, то = 0;
5.9. если = 1 и = 1, то = 0;
где 
, 
, 
.
В случае, если добавляемое соотношение уже имеет значение, полученное на этапе построения вспомогательной матрицы, производится генерация сообщения о нарушении условия транзитивности.
Найденные в результате реализации алгоритма пары объектов, нарушающие условие транзитивности, исключаются либо алгоритмически, либо на основе интерактивного диалога с экспертом. Во втором случае будет выводиться сообщение о противоречии с указанием пар соотношений, в которых произошло нарушение транзитивности.
Оценка неполноты экспертных высказываний проводится после проверки нетранзитивности отношений на основе построенной матрицы Y по следующему правилам (6):
6.1. g = 1, h = 1, 
, где 
, 
;
6.2. если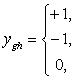 
, то 
, переход п.2.8.3, иначе 
;
6.3. если h = m + 1, то g = g + 1 переход п. 2.8.4, иначе h = h + 1, переход п. 2.8.2;
6.4. если g = m, то переход п. 2.8.5, иначе переход п. 2.8.2
6.5. вывод 
.
Здесь правило 6.2 устанавливает число h объектов, находящихся в соотношениях с g объектом вспомогательной матрицы Y.
Приведенный алгоритмический подход также может использоваться для согласованности групповых экспертных высказываний и является достаточно эффективным при экспертной оценке любого количества объектов исследования.