Противопожарная служба (ПС), являющаяся сложной социально-экономической системой, имеющей собственную инфраструктуру в целях экономии бюджетных средств должна эффективно распределять предоставляемые службе ресурсы, как и любой хозяйствующий субъект. Одной из задач распределения ресурсов, относящихся к деятельности ПС, является выбор маршрута движения пожарного автомобиля (ПА). Суть ее состоит в следующем: имеется n + 1 районов обслуживания (далее районов): А0 , А1, ..., Аn (n ³ 1) с заданными между ними расстояниями dij (i, j = 0, 1, 2, ..., n). Требуется, отправляясь из начального района A0 выбрать такой маршрут передвижения, при котором ПА, прибыв к месту привлечения, вернулся бы в исходный район A0, проделав минимально возможный суммарный путь. Как следует из общей характеристики задачи, минимизация времени на привлечение всех подразделений ПС является критерием оптимальности задачи ЛП. Определение минимального маршрута пути следования ПА должно осуществляться с картографическим обоснованием вариантов привлечения и применения следующего алгоритма, состоящего из двух этапов.
Первый этап.
1. Рассматривается два района: первый – район, из которого осуществляется привлечение; второй – район, требующий привлечение. На их основе строятся все возможные варианты движения ПА. m = 1.
2. Определяется минимальный маршрут следования для рассматриваемой пары районов по правилу:
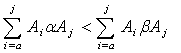 (1)
(1)
Здесь: α и β – соответствующие совокупности районов через которые следует ПА от района дислокации (Ai) до района привлечения (Aj). Очевидно, что α ~ β;
3. Если рассмотрены все привлекаемые подразделения – переход п.4, в противном случае – п.1.
4. На основе полученных комбинаций вариантов движения ПА определяем порядок привлечения по 1-му номеру вызова для рассматриваемого района. Переход к следующему району, требующему привлечение.
5. Если рассмотрены все районы, требующие привлечение, то m=m+1 и переход п.6, в противном случае – п.1.
Второй этап.
6. Рассматривается привлечение подразделений ПС по повышенному номеру вызова. На основе перспективных вариантов движения ПА, полученных на 1-ом этапе алгоритма, строятся все возможные варианты движения ПА для привлечения m-подразделений.
7. Определяется минимальный маршрут привлечения m-подразделений в рассматриваемый район. Переход к следующему району, требующему привлечение. Если рассмотрены все районы, требующие привлечение – завершение работы алгоритма, в противном случае – переход п.6.
Приведенный подход является эффективным инструментом решения задач в статической постановке. Однако, система обеспечения пожарной безопасности любого населенного пункта или административного района является динамической и, следовательно, требующей постоянного мониторинга состояния сил и средств подразделений ПС гарнизона. Основной проблемой при осуществлении такого мониторинга является одновременная занятость подразделений ПС обслуживанием вызовов. Динамический характер системы обуславливается сменой ее состояний. Будем рассматривать каждое состояние системы как некоторый вариант привлечения или занятости подразделений ПС гарнизона. При этом, оценивая тот или иной вариант, вместо определяемых значений переменных задачи ЛП будем использовать константы логического типа. Тогда математическую запись задачи ЛП по оптимизации распределения ресурсов ПС можно сформулировать следующим образом:
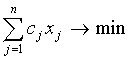 (5)
(5)
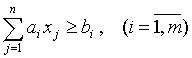 (6)
(6)
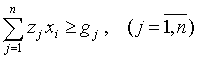 (7)
(7)
![]() (8)
(8)
Здесь: ![]() ограничение на количество привлекаемых подразделений в соответствующий район привлечения;
ограничение на количество привлекаемых подразделений в соответствующий район привлечения; ![]() коэффициенты целевой функции, принимающие значения времени привлечения соответствующего подразделения;
коэффициенты целевой функции, принимающие значения времени привлечения соответствующего подразделения; ![]() ограничение, устанавливающее количество привлекаемых подразделений;
ограничение, устанавливающее количество привлекаемых подразделений; ![]() коэффициенты, определяемые в результате решения задачи ЛП –
коэффициенты, определяемые в результате решения задачи ЛП – ![]() , если вариант принят,
, если вариант принят, ![]() , в противном случае.
, в противном случае.



