Социально-экономическое прогнозирование можно определить как процесс разработки прогнозов на основе научных методов познания экономических и социальных явлений и использования методов, способов и средств экономического прогнозирования.
Во временном разрезе прогнозы подразделяются:
● на краткосрочные (от 1 квартала до 1 года);
● среднесрочные (от 1 года до 5 лет);
● долгосрочные (от 5 лет до 20 лет).
При комплексном экономическом прогнозировании применяют следующую классификацию: краткосрочное прогнозирование имеет горизонт до 3 лет, среднесрочное – до 7 лет, долгосрочное – до 20 лет. Виды прогнозов опираются на устойчивые процессы и циклы в развитии экономики, укладывающиеся в соответствующий временной горизонт [1, 2].
Целью исследования является построение модели долгосрочного прогнозирования на основе методов регрессионного анализа с учетом трендов. На основе разработанной модели построен долгосрочный прогноз показателя ВВП России.
Методы прогнозирования – это приемы и способы, позволяющие выводить суждения о будущем состоянии и развитии объекта прогнозирования на основе данных внешних и внутренних связей объекта за прошедший период, а также их значений при рассмотрении явления или процесса.
При прогнозировании ВВП следует учитывать ряд особенностей. Во-первых, большой размер массива данных. Существует большое количество переменных для прогнозирования динамики ВВП, которые при этом еще и взаимосвязаны между собой. Массивы данных могут включать в себя более 300 переменных.
Во-вторых, существуют индикаторные переменные, которые наблюдаются более часто (ежемесячно, еженедельно, ежедневно), чем показатели ВВП.
Для формирования конечного прогноза проводятся два преобразования массива данных: агрегирование и применение инструмента прогнозирования, который привязывает вспомогательные переменные к реальному росту ВВП. Эти два преобразования могут быть выполнены в любом порядке, что соответствует двум принципиально разным стратегиям. В рамках первой стратегии работа начинается с вычисления индикаторного прогноза динамики ВВП для каждой из переменных, после чего на втором этапе эти прогнозы объединяются в единый финальный прогноз. Назовем эту стратегию «стратегией объединения прогнозов». При ее использовании необходимо определить схему взвешивания отдельных прогнозов. Базовая схема заключается в вычислении среднего арифметического, в результате чего все прогнозы имеют одинаковый вес; однако веса также могут быть вычислены рекурсивно в зависимости от прогностической эффективности индикаторов (за последнее время). В качестве примера стратегии объединенных прогнозов можно привести использование бридж-уравнений и VAR-моделей. В противоположность вышеописанному в рамках «стратегии агрегации информации» на первом этапе проводится разбивка информации на группы путем разделения большого массива данных на небольшое количество рядов. Эта стратегия основывается на том факте, что вспомогательные переменные коррелированы [9]. Для замены большого количества коррелированных временных рядов ограниченным количеством некоррелированных (ненаблюдаемых) факторов используется факторный анализ. Неявные веса (факторные нагрузки) определяются из корреляционных схем в оригинальном массиве данных. Факторы служат в качестве входных данных для выполнения прогнозирования на следующем этапе. В качестве примера данной стратегии можно привести использование динамической факторной модели и дополненных факторами версий прогностических моделей, которые объединяются в прогнозы. В последнее время стала применяться оценка с использованием байесовского стягивания по коэффициентам, при которой большой массив индикаторов переводится непосредственно в единый прогноз динамики ВВП без явно выраженного этапа агрегации. При таком подходе агрегация информации происходит неявно путем байесовского стягивания к параметрам.
Традиционные подходы, такие как использование бридж-моделей и VAR-моделей, строятся на базе прогностических уравнений, которые составляются строго в квартальных рамках. Это означает, что (прогнозы) месячных значений переменных индикаторов до того, как они могут быть использованы для прогнозирования динамики ВВП, должны быть сперва агрегированы в среднеквартальные показатели [8]. Кроме того, в квартальных VAR-моделях доступные месячные наблюдения не используются в полной мере. Так как указанное не может представлять собой эффективное использование доступной информации, в последнее время были разработаны подходы, сочетающие в себе как квартальные, так и месячные показатели в рамках одного и того же уравнения или системы уравнений. Такие подходы также учитывают временные лаги. В рамках VAR-модели со смешанной частотой (MFVAR-модель) ВВП рассматривается как ненаблюдаемая месячная переменная в пространстве состояний.
Обзор квартальных моделей роста ВВП
Бридж-уравнение (BEQ-модель). Составление квартального бридж-уравнения – это метод, широко используемый для прогнозирования динамики ВВП с применением всех доступных наблюдений месячных индикаторов.
Бридж-уравнения представляют собой линейные регрессии, которые «образуют мосты» (от английского слова «bridge» – «мост») между месячными переменными, такими, как надежность производства и розничные продажи, и квартальными показателями динамики реального ВВП. Обычно месячные индикаторы известны для всего горизонта [7]. Проанализируем простую версию бридж-уравнения, когда оно применяется в два этапа. Сначала получаем прогноз обязательных месячных значений индикатора xi в рамках горизонта прогнозирования при помощи однофакторных авторегрессионных моделей и агрегируем их в соответствующие квартальные значения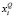 
. Затем используем эти среднеквартальные значения для прогнозирования динамики ВВП. Бридж-модель для xi имеет следующий вид:
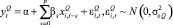, (1)
где α – константа;
р – количество лагов в бридж-уравнении;
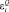– нормально распределенная величина погрешности.
Составляем уравнение (1) для каждого из n индикаторов, а затем вычисляем конечный прогноз путем взвешивания n индикаторных прогнозов для каждого горизонта. Параметр лага р определяется рекурсивно при помощи информационного критерия Шварца (SIC) с заданным максимальным количеством лагов, равным четырем.
Векторная авторегрессионная модель (QVAR-модель). VAR-подход очень похож на подход через составление бридж-уравнения. В отличие от бридж-уравнений в VAR-моделях для формирования прогнозов динамики ВВП используется информационное содержание самого ВВП. Кроме того, это системный подход, в рамках которого используются взаимосвязи между динамикой показателей индикаторов и реального ВВП. В связи с квартальными временными рамками в QVAR-модели используются только месячные наблюдения, соответствующие целому кварталу. Следовательно, в модели доступная месячная информация не используется в полной мере [6]. Оценим n квартальных двумерных VAR-моделей, включающих один из индикаторов и показатели роста ВВП:
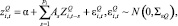(2)
где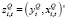 
.
На основании каждой двумерной VAR-модели составляем прогноз динамики ВВП по каждому индикатору, а именно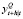 
. Как и в случае бридж-модели, формируем финальный прогноз как взвешенное среднее отдельных прогнозов. Параметр лага р определяется рекурсивно при помощи информационного критерия Шварца (SIC) с заданным максимальным количеством лагов, равным четырем.
Модели со смешанной частотой. В последние годы растет интерес к моделям со смешанной частотой в связи с общей неспособностью простых квартальных моделей прогнозировать глубокий упадок экономики в начале финансового кризиса или сигнализировать о таком упадке. Авторы Д. Джансен, Х. Джин, Д. Винтер [10] провели анализ подходов к прогнозированию с использованием динамической факторной модели, VAR-модели со смешанной частотой и MIDAS-модели. Во всех этих моделях доступная месячная информация используется в полном объеме.
В динамических факторных моделях информация, содержащаяся в массиве данных, обобщается при помощи ограниченного количества факторов, динамическое поведение которых определяется как вектор-авторегрессионные процессы. Ключевой особенностью данного подхода является использование фильтра Калмана, что позволяет эффективно справляться с проблемами, связанными с несбалансированностью массива данных и различными частотами данных. При помощи фильтра Калмана любые отсутствующие месячные наблюдения индикаторов заменяются оптимальными прогнозами, а также генерируются оценки ненаблюдаемых месячных показателей динамики реального ВВП при условии наличия временнóго ограничения агрегации в рамках квартального наблюдения. Динамические факторные модели позволяют получать относительно точные макроэкономические прогнозы для многих стран. Рассмотрим динамическую факторную модель, которая используется некоторыми центральными банками в границах еврозоны. Первое уравнение этой модели имеет следующий вид:
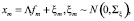
где n месячных индикаторов xm соотносятся с r месячных статических факторов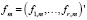 
через матрицу факторных нагрузок Ʌ и (специфическую) компоненту 
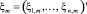при r << n. В рамках DFM-модели предполагается, что специфические компоненты представляют собой многомерный процесс белого шума, следовательно, ковариационная матрица 
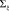диагональна. Кроме того, в рамках DFM-модели предполагается, что факторы подчиняются вектор-авторегрессионному процессу порядка р:
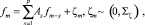
где А является квадратной матрицей r x r. Кроме того, ковариационная матрица VAR (σζ) управляется q-размерным стандартизированным процессом белого шума ηm:
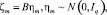
где В является матрицей r x r, а q ≤ r. Последнее уравнение – это прогностическое уравнение, объединяющее факторы в (ненаблюдаемые) уравненные по среднему значению показатели роста реального ВВП:
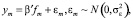
где ym означает ненаблюдаемые месячные темпы роста ВВП. Модель оценивается в четыре этапа. На первом этапе получают факторные нагрузки Ʌ и оцениваемые статические факторы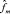 
. На втором этапе оценивают матрицы коэффициентов 
по методу наименьших квадратов с использованием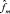 
. На третьем этапе вычисляется значение ζm, составляется ее ковариационная матрица ζm и путем анализа принципиальных компонентов оценивается матрица В. На последнем этапе модель помещается в пространство состояний и для повторной оценки оцениваемых факторов (
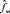) и месячного роста ВВП применяется фильтр Калмана и сглаживающий фильтр.
Инновационная модель прогнозирования
Разработаем модель долгосрочного прогнозирования на основе методов регрессионного анализа с учетом трендов. Модель строится на основе совокупности линейного, логарифмического и гармонического трендов и рассчитывается посредством последовательной трендовой декомпозиции. Прогноз представляет собой совокупность трендов, описывающих движение стоимости актива [3–5].
В таком прогнозе в виде трендов учтены общие тенденции движения актива, пороги насыщения, периодические составляющие. Представлена функция прогноза как совокупность насыщаемого (логарифмического), не насыщаемого (линейного) и гармонического трендов:
y = yлог + yлин + yгарб,
тогда
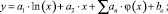
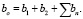
На основе предложенной модели долгосрочного прогнозирования сделаем прогноз по Валовому внутреннему продукту. Данные взяты из источника Государственной службы Федеральной статистики.
Рассчитаем прогноз ВВП, представленный годовыми значениями. На рис. 2 и 3 проиллюстрирован результат прогнозирования показателя ВВП России.
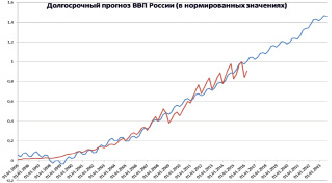
Рис. 1. Результат прогноза показателя Валовой внутренний продукт (квартальные данные), выраженный в нормированных значениях
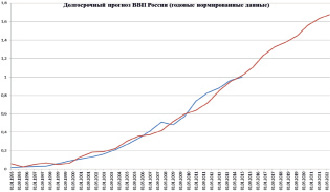
Рис. 2. Результат прогноза показателя Валовой внутренний продукт (годовые данные), выраженный в нормированных значениях
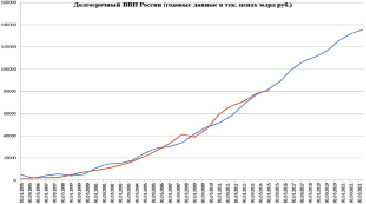
Рис. 3. Результат прогноза показателя Валовой внутренний продукт (годовые данные), выраженный в текущих ценах (млрд руб.)
Таким образом, проведя обзор моделей прогнозирования ВВП, можно прийти к выводу, что статистические модели обладают большей ценностью, если в них может использоваться информация, относящаяся к соответствующему кварталу. Их относительные преимущества заключаются в повышении эффективности оценки состояния экономики в данный конкретный момент времени. Динамические факторные модели в целом обладают большей эффективностью. В масштабах разных стран и горизонтов такая модель наилучшим образом работает для ретроспективного прогнозирования. В работе также предложена авторская модель долгосрочного прогнозирования.
Статья подготовлена по результатам исследований, выполненных за счет бюджетных средств по Государственному заданию Финансового университета при Правительстве Российской Федерации в части проведения НИР по теме: «Моделирование долгосрочного социально-экономического развития России».