Электрогидравлические следящие приводы нашли широкое применение в качестве силовых устройств в системах управления различными объектами и технологическими процессами, и, следовательно, качество таких систем управления будет зависеть от динамики привода. Поэтому при проектировании систем управления повышаются требования к динамическим показателям приводов, а также к адекватности математической модели привода. В случае решения задачи проектирования известна структура привода и в качестве определяемых параметров выступают геометрические размеры отдельных элементов, числовые значения которых определяются из условия обеспечения динамических характеристик привода, соответствующих техническому заданию. В случае построения адекватной математической модели часто известна структура модели, и задача идентификации сводится к задаче уточнения числовых значений некоторых параметров модели. В обоих случаях можно сформулировать следующую задачу. Известна структура привода; известен закон изменения напряжения, подаваемого на вход; известен (задан) закон перемещения выходного звена привода. Требуется определить числовые значения параметров привода из условия максимального приближения сигнала на выходе модели привода к заданному. В качестве меры близости можно взять функционал
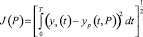, (1)
где yэ(t) – заданный закон изменения выходной координаты; yp(t, P) – сигнал на выходе привода; P – множество искомых параметров.
При проектировании привода в качестве искомых конструктивных параметров часто выступают такие, как площадь рабочей поверхности поршня, которая определяется диаметром штока и внешним диаметром поршня, условный диаметр золотникового пропорционального распределителя, жесткость позиционной нагрузки и параметры настройки усилителя и датчика обратной связи, а также параметры регуляторов, вводимых для улучшения динамики привода. В случае задачи параметрической идентификации к уточняемым параметрам можно отнести параметры, существенно зависящие от температуры и условий эксплуатации: коэффициенты вязкого трения подвижных частей привода, характеристики рабочей жидкости (её плотность и модуль объемной упругости), параметры, характеризующие процесс течения жидкости, а также коэффициенты настройки некоторых элементов привода (электронного усилителя и датчика обратной связи).
Однако в случае использования управляемого насоса в качестве источника давления выход yp(t, P) будет зависеть от характеристики такого насоса, которая определяется такими величинами, как номинальная подача насоса при отсутствии нагрузки и номинальное давление. Последний показатель можно определить из требований к максимальному усилию, развиваемому гидроприводом, а номинальную подачу определяют со значительным запасом, что может отразиться на стоимости привода в целом. Поэтому данный показатель насоса также можно определить из условия обеспечения требуемых динамических показателей привода, которое в дальнейшем будет определяться в требованиях как желаемый показатель насоса. Следовательно, к уравнению баланса расходов необходимо добавить характеристику насоса, которая показывает значение текущего давления нагнетания от подачи рабочей жидкости, отдаваемой потребителю.
Ниже рассматривается подход к определению числовых значений конструктивных параметров и настраиваемых параметров электрогидравлического следящего привода (ЭГСП) с учётом характеристики насоса с использованием проекционных методов. Проекционный метод, или метод матричных операторов, нашёл широкое применение в силу ряда достоинств, к которым можно отнести переход от рассмотрения временных функций к их спектральным характеристикам, представляющим собой коэффициенты Фурье относительно элементов выбранного базиса, что позволяет заменить операции над функциями операциями над матрицами и даёт возможность реализации на электронно-вычислительных машинах и, тем самым, позволяет упростить решения задач анализа и синтеза. Кроме того, проекционный метод обладает хорошей сходимостью и обеспечивает требуемую точность расчёта, что отражено в соответствующей литературе, указанной в [3, 4].
Математическая модель привода
Конструктивно ЭГСП состоит из исполнительного гидродвигателя – гидроцилиндра; пропорционального золотникового распределителя; электронного усилителя в прямой цепи и датчика обратной связи, контролирующего текущее положение выходного звена – штока гидроцилиндра. Соответственно, математическая модель привода будет включать уравнения описывающие процессы, протекающие в распределителе и гидроцилиндре, а также уравнение баланса расходов рабочей жидкости, протекающей через распределитель, и уравнение обратной отрицательной связи.
Модель пропорционального золотникового распределителя и обратной связи можно представить уравнением
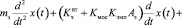
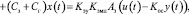(2)
где u(t) – напряжение, подаваемое на вход привода; x(t) – перемещение золотника гидравлического дросселирующего распределителя, причём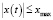 
(xmax – максимальная ширина открываемой буртом золотника щели); y(t) – перемещение штока гидроцилиндра; Kэу – коэффициент передачи электронного усилителя; Kос – коэффициент передачи обратной связи (датчика); 
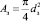– площадь торца золотника, а dз – его диаметр; mз – масса золотника; 
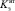– коэффициент вязкого трения между золотником и втулкой; Сз – суммарная жесткость пружин, на которые опирается золотник; Сг – жесткость гидравлической пружины; Kэмп – коэффициент передачи первого каскада электрогидравлического усиления (ЭГУ), включающего электромеханический преобразователь (ЭМП), распределитель сопло-заслонка; Kмос – коэффициент передачи местной обратной связи, обусловленной особенностями протекающих процессов. Замена ЭМП и распределителя сопло-заслонка пропорциональным звеном возможна в силу быстроты протекающих в них процессов по сравнению с процессом движения золотника распределителя, что подтверждается соответствующим моделированием.
Уравнение движения выходного звена гидроцилиндра имеет вид
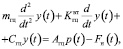(3)
где p(t) – перепад давления на поршне гидроцилиндра; Fн(t) – внешняя нагрузка, действующая вдоль оси штока; mгц – масса подвижных частей гидроцилиндра; 
– коэффициент вязкого трения гидроцилиндра; Сгц – коэффициент позиционной нагрузки; Агц – площадь рабочей поверхности поршня.
Уравнение баланса расходов рабочей жидкости, протекающей через распределитель, имеет вид [1, 2]:
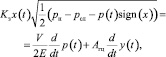(4)
где Kз – удельная проводимость окон золотникового дросселирующего распределителя; V – объём полостей гидроцилиндра и подводящих трубопроводов; E – модуль объёмной упругости рабочей жидкости; pн – давление нагнетания; pcл – давление в дренажной линии.
В приведённом уравнении давление нагнетания pн не является постоянной величиной, а зависит от расхода жидкости, отдаваемой насосом потребителю. В случае использования неуправляемого насоса данная зависимость несущественна и ей можно пренебречь, при использовании насоса с управлением зависимость pн(Q) существенна и будет влиять на динамику привода. Поэтому при составлении уравнения баланса расходов данный факт необходимо учитывать. В результате уравнение примет вид 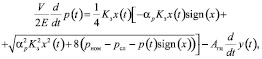[5]:
(5)
где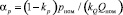 
, pном и Qном – соответственно номинальные давление и расход насоса, kQ и kp – коэффициенты, характеризующие жесткость расходных характеристик гидронасоса и предохранительного клапана соответственно.
Таким образом, получим следующую модель ЭГСП:
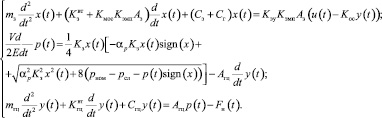(6)
В случае использования регуляторов систему уравнений (6) необходимо дополнить соответствующими уравнениями.
Расчёт оптимальных значений параметров привода
Очевидно, что полученная модель привода является существенно нелинейной, что затрудняет применение проекционных методов для решения задач анализа и синтеза (в нашем случае задачи определения числовых значений конструктивных параметров привода из условия обеспечения требуемых динамических характеристик).
Линеаризуем уравнение расходов путём представления в виде степенного ряда с удержанием линейных слагаемых. В результате получим
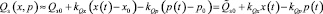, (7)
где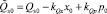 
; 
,
.
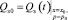
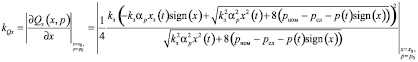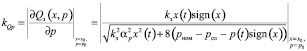Очевидно, что значения коэффициентов kQx, kQp и постоянной составляющей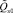 
зависят от выбора x0 и p0.
В результате систему уравнений (6) можно записать в виде
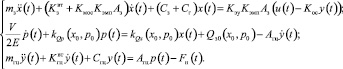(8)
Кроме того предполагается, что привод работает в режиме, при котором выполняются ограничения
; 
.
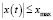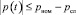Выбрав некоторый ортонормированный базис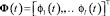 
и переходя к рассмотрению спектральных характеристик сигналов [3, 4] в выбранном базисе, получим следующую систему уравнений в операторной форме
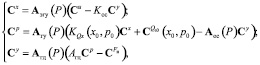(9)
где Aэгу(Р) – матричный оператор в выбранном базисе, эквивалентный передаточной функции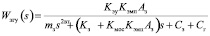 
; Aгу(Р) – эквивалентный 
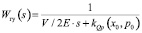; оператор Aос(Р) эквивалентен Wос(s) = Aгцs; оператор Aгд(Р) эквивалентен 
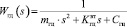; P – множество определяемых параметров привода.
Из системы (9) находим спектральную характеристику Cy, которая определяется зависимостью
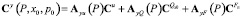, (10)
где
;
; 
;
.
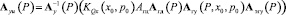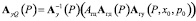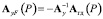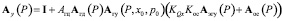Тогда [3], функционал (1) примет вид
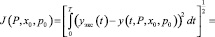
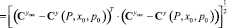. (11)
Следовательно, задача определения числовых значений конструктивных параметров сводится к задаче условной оптимизации функционала (11) на множество допустимых значений параметров P.
Однако критерий J(P, x0, p0) зависит от точки линеаризации расходно-перепадной характеристики распределителя x0 и p0. Как показано в [5], значения x0 и p0 можно уточнить на каждом шаге итерации поискового алгоритма методом последовательных приближений.
Изложенный выше подход использован для уточнения числовых значений некоторых параметров модели ЭГСП, представленной системой уравнений (6). Реакция привода на ступенчатое воздействие с конечным значением 10 В представлена на рисунке. В качестве уточняемых параметров привода рассматривались следующие: плотность рабочей жидкости ρ и модуль объёмной упругости E, которые зависят от марки используемой рабочей жидкости и количества растворенного в жидкости воздуха; коэффициенты вязкого трения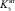 
и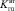 
, существенно зависящие от температуры; коэффициенты Kэмп и Kмос, зависящие от ряда параметров, не подлежащих измерению; коэффициент расхода щели золотникового распределителя μ, зависящего от геометрии щелей золотника и втулки (в справочной литературе задаётся в виде диапазона значений). При решении поставленной задачи использовался базис блочно-импульсных функций с удержанием 200 элементов, время расчёта составило порядка одной минуты при решении задачи на компьютере на базе процессора CPU Intel Core i3 2.10GHz, RAM 4.0 GB. Алгоритм реализован в системе MATLAB® (The MathWorks Inc.) версии 8.6 (R2015b). На рисунке представлены графики выходного сигнала привода для начальных (справочных) значений уточняемых параметров и для найденных оптимальных значений.
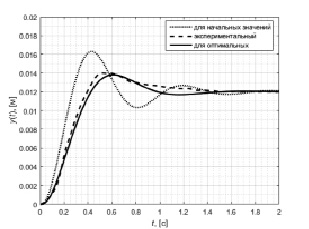
Графики выходного сигнала привода
Заключение
Применение проекционных методов позволило свести задачу определения оптимальных числовых значений параметров ЭГСП с учётом влияния характеристики насоса к задаче условной оптимизации на множестве допустимых значений искомых (уточняемых) параметров. Переход от исходной модели привода, представленной системой дифференциальных уравнений (8), к операторной форме записи (11) значительно упрощает расчёт целевой функции (1). Эффективность построенного алгоритма подтверждена результатами решения задачи уточнения числовых значений некоторых параметров привода на основе экспериментальных данных. Предложенный подход также может быть использован для решения задач синтеза или параметрической идентификации целого класса нелинейных систем управления и объектов, к которым относится электрогидравлический следящий привод.