В технических устройствах со сложной механикой [6, 15, 20] почти всегда есть место для возникновения автоколебаний. Изучением колебаний, возникающих в процессе бурения, занимались многие ученые [4].
При работе шарошечного долота различают следующие колебательные процессы, обеспечивающие динамическое воздействие на забой [18]:
а) высокочастотные, появление которых вызвано зубчатостью шарошек;
б) среднечастотные, природа которых связана с изменением во времени числа взаимодействующих с поверхностью забоя скважины зубьев долота;
в) низкочастотные, обусловленные возникновением вследствие неоднородности строения горных пород и их дефектности ухабов на забое скважины.
В процессе бурения эти колебания могут привести к ухудшению основных показателей. Опасность любых автоколебаний в том, что они ведут к разрушению, износу деталей бурового инструмента, увеличению технологических зазоров, повышенной и нерациональной трате энергии [11]. При этом уменьшить амплитуду этих колебаний наиболее эффективно можно согласованием конструкции и массогабаритных показателей, но только при знании спектра частот [1–3, 5, 12].
С другой стороны, колебательные процессы, возникающие в системе «долото – забой», способны интенсифицировать бурение [13, 17]. Моделирование и расчет возникающего при этом напряженно-деформированного состояния приведены в [8, 9, 12, 21].
Наконец, знание спектра частот возникающих автоколебаний позволяет снизить помехи при использовании нового способа передачи информации с забоя [19] посредством механико-гидравлического (МГ) канала связи о таких параметрах забойного процесса, как частота вращения долота и его шарошек, амплитуда осевых колебаний корпуса долота, твердости разбуриваемых горных пород и т.д.
В устройстве для реализации способа бурения разновращающимися буровыми коронками, находящемся под разносторонней и интенсивной нагрузкой в технологическом процессе, главную роль играют крутильные колебания. В этом инструменте разное направление вращения буровым коронкам придано для снятия реактивного момента со шланга при шланго-кабельном бурении. Из-за наложения колебаний на такую систему управление ей становится особенно сложным [10].
Теория
Для снятия реактивного момента, возникающего при бурении скважины, было разработано специальное устройство [7]. В этом устройстве забой разбуривается двумя коронками – круговой и кольцевой, вращающимися в разные стороны. При этом в зависимости от загруженности разбуриваемая ими площадь перераспределяется в сторону увеличения для слабонагруженной коронки и уменьшения площади, разбуриваемой перегруженной коронкой. Перераспределение производится автоматически при появлении разности в угловых скоростях вращения коронок с помощью дифференциального механизма и винтовой линии с углом наклона α, преобразующими изменения скорости вращения коронок в вертикальное движение поводков, одновременно поворачивающих буровые коронки круговой и кольцевой частей и меняющих площади их разбуривания, а вместе с ними перераспределяющих величину реактивных моментов.
Схемой, моделирующей механизм возникновения автоколебаний в рассматриваемом буровом инструменте, являются упруго-скрепленные сплошной и полый цилиндры, лежащие на вращающихся диске и кольце соответственно, изображенные на рис. 1.
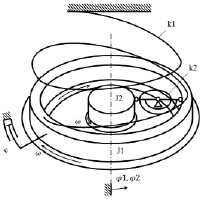
Рис. 1. Модель автоколебательной системы
При этом пружина k2 с двумя стержнями имитирует сателлит дифференциального механизма, связывающий держатели буровых коронок (солнечные колеса) и позволяющий им вращаться в разные стороны.
Схема является обращенной по отношению к процессу бурения, при котором вращаются модельные цилиндры, несущие в нижней части буровые коронки, а дно забоя неподвижно. Трение происходит между буровыми коронками и забоем.
Качественное объяснение механизма возбуждения автоколебаний в таких схемах было высказано Рэлеем [16] на примере смычковых инструментов. Он считал, что «способность смычка поддерживать колебания струны связана с тем, что трение при средних скоростях меньше, чем при малых».
Опираясь на исследование прямолинейных автоколебаний в двухмассовой системе [16], проанализируем крутильные колебания в заявленном буровом инструменте. Механические модели, в которых возникают автоколебания под действием трения скольжения получили название «stick-slip» («прилипание-скольжение»), в силу того, что в них наблюдается два вида движения: когда цилиндры неподвижны относительно вращающихся диска или кольца и когда они скользят по ним.
Рассматриваемая модель состоит из двух соосных цилиндров – полого и сплошного с моментом инерции J1 и J2 соответственно. Полый цилиндр с моментом инерции J1 соединен с неподвижной опорой невесомой круговой пружиной с жесткостью k1, а сплошной цилиндр с моментом инерции J2 соединен с полым цилиндром с моментом инерции J1 двумя стержнями, связанными друг с другом пружиной жесткости k2. Цилиндр J2 находится на вращающемся с угловой скоростью ω диске, а цилиндр J1 – на кольце, вращающемся с той же угловой скоростью в противоположную сторону. Повороты цилиндров из положения, в котором пружины не деформированы, обозначим φ1 и φ2 (рис. 1). Между первым цилиндром и неподвижной опорой действует сила вязкого трения с коэффициентом с, а между цилиндрами и вращающимися диском и кольцом действует сила трения скольжения f.
Примем кусочно-постоянную модель трения скольжения с коэффициентом трения в виде [16]
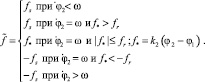
Здесь точка сверху означает дифференцирование по времени координаты второго груза (для первого груза имеют место такие же соотношения), fs и fr – коэффициенты трения скольжения и покоя, пропорциональные нормальному давлению, причем коэффициент трения скольжения не больше коэффициента трения покоя (fs ≤ fr ).
Уравнения движения исследуемой системы
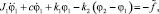
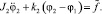(1)
В отличие от работы [16], постановка этой задачи относится к крутильным колебаниям и отличается наличием трения в обоих уравнениях правой части. Уравнения решаются для случая
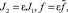
где ε – малая положительная величина.
Материалы и методы исследования
Как показано в той же работе, второе уравнение описывает нелинейные незатухающие колебания с периодом
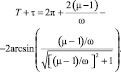
Он зависит от отношения (μ – 1)/ω (разности коэффициентов трения покоя и скольжения {μ = fr/fs} к угловой скорости ленты). Сразу можно сделать вывод: чем меньше угловая скорость ленты ω, тем в большем диапазоне изменяется период при изменении μ, и чем больше угловая скорость ленты, тем в меньшем диапазоне изменяется период при изменении μ.
Первое уравнение в (1) в безразмерных координатах и после подстановки решения второго уравнения примет вид уравнения вынужденных колебаний при наличии трения скольжения
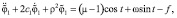
при 0 ≤ t ≤ T,
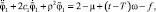
при T ≤ t ≤ T + τ, (2)
где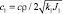 
и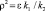 
.
Для нахождения решения уравнений (2) можно применить метод, описанный в [14]. Примем
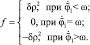
Тогда левая часть уравнений примет вид
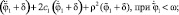
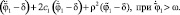(3)
Отсюда следует, что левая часть уравнения (2) описывает затухающие колебания, фокус которых сдвинут по оси ординат в фазовых координатах на величину δ влево от начала координат в верхней части фазовой плоскости и вправо – в нижней части. При этом необходимо помнить, что когда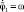 
, сила трения останавливает первый цилиндр по отношению к вращающемуся диску и он движется с его угловой скоростью, при этом трение как слагаемое в правой части уравнений (2) пропадает.
Ввиду громоздкости получающихся формул движение без силы трения скольжения на первом грузе было исследовано в [16] численно. Показано, что при с1 > 0 во всех трех возможных случаях (с2 < ρ2, с2 = ρ2 и с2 > ρ2) наблюдается устойчивость вынужденных колебаний первого груза при всех значениях параметров ρ, μ, ω. При малых с скорость стремления фазовых траекторий к вынужденному движению мала, а при его увеличении возрастает. Эта скорость увеличивается при возрастании μ, уменьшении ω и не зависит от ρ.
Для качественного анализа решения уравнений (2) с левой частью в виде (3) была использована программа МВТУ [3] с моделирующей схемой, изображенной на рис. 2.
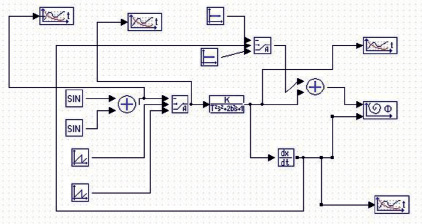
Рис. 2. Моделирующая схема в МВТУ 3.7
Поведение первого (кольцевого) цилиндра описывается колебательным звеном, переходной процесс запускается ступенчатыми сигналами и синусоидальными в качестве вынуждающих, то есть описывающих воздействие внутреннего цилиндра, блоки для графического вывода информации, нанесенные на схему в указанных местах, предусмотрены для диагностики. Буквой А на схеме помечены ключи, изменяющие прохождение входных сигналов при удовлетворении пороговых условий. При этом управляющим является средний входной сигнал – когда он превышает заданное пороговое значение, выходной сигнал переключается с верхнего входного по схеме на нижний. Ключи реализуют изменение уравнений при пересечении аргументами осей координат фазовой плоскости.
Результат – колебания второго звена – выводится и оценивается на фазовой плоскости, при этом для организации второй координаты используется дифференцирующее звено.
Результаты исследования и их обсуждение
Полученный график переходного процесса в фазовых координатах (см. рис. 3) показывает, что колебания со временем выходят на установившийся цикл, представляют полигармоническое поведение первого груза со сложным спектром. Хотя, в соответствии со схемой рис. 2, случай превышения цилиндрами угловой скорости вращения кольца и пониженной по сравнению с ним скоростью необходимо рассматривать отдельно (на рис. 3 это отражено сдвигом графика на уровне 1), а решения «сшивать», все же периоды главных гармоник легко можно оценить.
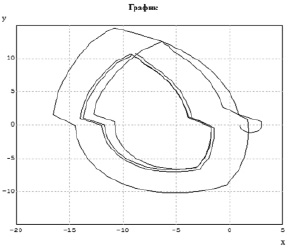
Рис. 3. График вынужденных колебаний первого цилиндра в фазовых координатах
Кроме того, в [16] численно доказано, что при различных значениях параметров, кроме случая отсутствия вязкого трения, в котором требуется дополнительное исследование, вынужденные колебания первого цилиндра устойчивы, причем скорость сходимости соседних фазовых траекторий к предельному циклу прямо пропорционально зависит от разности коэффициентов трения покоя и скольжения и обратно пропорционально от угловой скорости дисков.
Заключение
Таким образом, проведенное исследование позволяет сделать вывод о возможности управляемого численного определения и изменения спектра возникающих автоколебаний. Последнее возможно путем изменения соотношения и геометрии расположения масс элементов конструкции, жесткости соединений этих элементов, коэффициента демпфирования, а также скорости вращения с целью конструктивной оптимизации рассматриваемого бурового инструмента и, соответственно, целенаправленного изменения его динамических характеристик. Исследование можно продолжить в направлении возникновения вынужденных колебаний, связанных с неоднородностями буримой породы.