В современных условиях крупным мультимодальным транспортным компаниям свойственны функции логистического посредника и дистрибьютора. Эти функции порождают задачи повышения эффективности управления заказами на операционную обработку грузов и определения оптимизированных размеров подлежащих хранению товарных партий [1, 5]. Мультимодальная перевозка – это транспортировка грузов по одному договору, но выполненная по меньшей мере двумя видами транспорта (например: железной дорогой, морем и автодорогой и т.д.), при этом перевозчик несет всю ответственность за перевозку, даже если эта транспортировка производится разными видами транспорта. Перевозки грузов в смешанном транспортном сообщении, или мультимодальные перевозки, – это стратегически важный вид транспортной деятельности. Одна из задач развития транспортной отрасли – увеличение объема мультимодальных перевозок грузов, так как это позволяет снизить дисбаланс между различными видами транспорта и тем самым оптимизировать транспортную систему в целях удовлетворения потребностей как экономического роста, так и устойчивого развития. Таким образом, современное развитие транспортной отрасли нацелено на расширение использования мультимодальных перевозок. Мультимодальные перевозки представляют собой комплекс логистических решений, подразумевающий транспортировку груза различными видами транспорта на разных этапах пути. Выбор транспортных средств осуществляется на основе временных и финансовых показателей с целью оптимизации денежных затрат и достижения наибольшей оперативности доставки. Данный тип перевозок часто используется при международных поставках. Все больше импортеров и экспортеров стремятся упростить для себя процесс транспортировки груза, доверяя его осуществление только одному экспедитору, при этом возлагая на него всю ответственность за своевременную доставку груза и риски, связанные с процессом перевозки. Кроме того, минимальный уровень транспортной инфраструктуры в стране должен отвечать всем соответствующим международным стандартам для того, чтобы в полной мере использовать все преимущества мультимодальных перевозок. Эти преимущества позволят экспортеру быть более конкурентоспособным, так как неся минимальные затраты, в минимальные сроки он сможет обеспечить доставку товара иностранному покупателю. А импортеру преимущества мультимодальных перевозок позволят сэкономить временные и финансовые затраты, так как груз будет доставлен вовремя и при минимальных денежных затратах. Чтобы оставаться конкурентоспособными, экспортеры и импортеры должны сокращать транспортные расходы, которые включены в стоимость товара, если цена определена с доставкой. Для того чтобы устранить такие скрытые издержки, рассматриваемому региону или стране необходимо повысить качество международных транспортных и логистических возможностей.
Рабочие бизнес-процессы мультимодальных транспортных компаний в странах и регионах с развитым морским и речным судоходством, разветвленными сетями водных путей сообщения, современной автодорожной инфраструктурой [8] и наличием железнодорожного транспорта, в качестве элементов цепочек обработки грузов включают промежуточные фазы складского хранения, различающегося по длительности, по специальным технологическим условиям и, соответственно, по стоимостным показателям, в полной мере свойственны стратегическому и тактическому планированию в транспортных компаниях Социалистической Республики Вьетнам и ряда соседних стран Юго-Восточного Азиатского региона [2, 4].
В статье представлена методика получения нечетко-множественных оценок для оптимизированного размера операционного заказа в мультимодальной транспортной сети с учетом затрат на содержание запаса на единицу площади или объема склада на базе применения эвристического принципа обобщения к специализированной версии формулы Уилсона [7] и описания нечетких экзогенных параметров расчетного соотношения нечеткими интервалами с трапецеидальными функциями принадлежности.
Нечеткая модель оптимизации размера операционного заказа в мультимодальной транспортной сети
Базовым соотношением рассматриваемой модели является апробированная методология определения оптимизированного количественного показателя Q объема операционного заказа в единицах с учетом затрат на содержание запаса на единицу площади или объема склада в условиях фиксированной длительности хранения, которая основывается на применении соответствующей специализированной модификации формулы Уилсона [7] вида
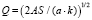, (1)
где S – объем потребности в запасе за рассматриваемый период в единицах; A – показатель затрат по выполнению одного заказа в денежном выражении, у.е.; a – показатель затрат на содержание единицы запаса с учетом занимаемой складской площади или объема в у.е./м2 или у.е./м3; k – показатель габаритов единицы запаса хранения соответственно в м2 или м3. Рассматриваемая модель базируется на предположениях об интерпретации экзогенных и эндогенного параметров модифицированного специализированного расчетного соотношения Уилсона (1) как нечетко-множественных характеристик, а также на применении к соотношению (1) эвристического принципа обобщения (принципа расширения) [2, 3, 6]. Согласно применяемому подходу область определения четкого классического функционального отображения (1) распространяется на аргументы, представляемые нечеткими множествами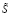 
, 
, 
, 
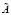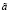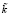с функциями принадлежности 
, 
, 
, 
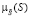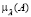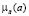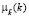, что позволяет получить для эндогенного параметра 
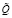описание в виде нечеткого множества с функцией принадлежности 
.
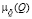Для описывающей исследуемую модель функциональной зависимости (1) применение общей схемы принципа расширения [12–13, 15] приводит к следующему представлению для характеризующей нечеткое множество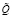 
функции принадлежности 
:
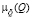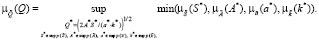(2)
В рассматриваемом случае схема использования принципа расширения эффективно алгоритмизируется с использованием представлений экзогенных нечетко-множественных характеристик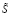 
, 
, 
, 
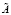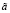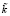в форме суперпозиции по множествам α-срезов:
, 
, 
, 
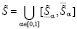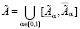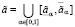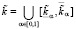. (3)
На основе представлений (3) для характеристики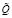 
записывается выражение:
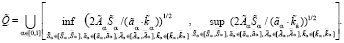(4)
Вид представления (1) позволяет использовать для определения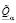 
, 
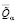удобную модификацию α-уровневой формы принципа обобщения [6], которая базируется на заключениях относительно свойств знакоопределенности для парциальных частных производных всем аргументам от представления (1) для Q, имеющих следующий вид:
,
,
,
,
.
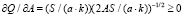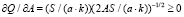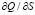
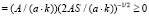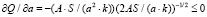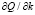
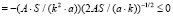Устанавливаемые свойства знакоопределенности позволяют записать следующие выражения для величин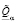 
, 
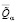в представлении 
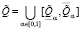для оцениваемой нечетко-множественной характеристики 
:
,
.
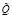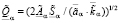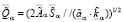Достаточная степень адекватности получаемых нечетких оценок может быть достигнута при описании неопределенных экзогенных параметров анализируемой модели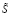 
, 
, 
, 
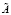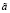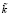нечеткими интервалами с трапецеидальными функциями принадлежности. В случае задания указанных нечетких интервалов кортежами реперных значений (А1, А2, А3, А4), (S1, S2, S3, S4), (a1, a2, a3, a4), (k1, k2, k3, k4) и соответствующего описания их разложениями по α-срезам:
,
,
,
.
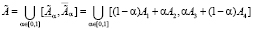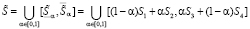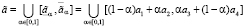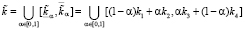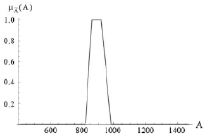
Рис. 1. Функция принадлежности для нечетко-множественной характеристики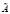 
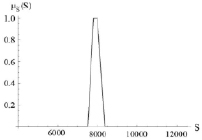
Рис. 2. Функция принадлежности для нечетко-множественной характеристики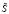 
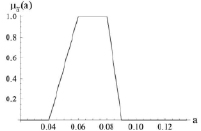
Рис. 3. Функция принадлежности для нечетко-множественной характеристики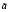 
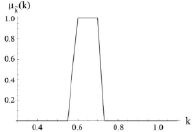
Рис. 4. Функция принадлежности для нечетко-множественной характеристики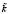 
Величины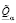 
, 
:
,
.
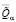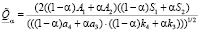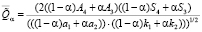Полученные представления описывают нечеткую оценку для оптимизированного показателя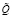 
, размера операционного заказа в мультимодальной транспортной сети с учетом затрат на содержание запаса на единицу площади или объема склада и с учетом факторов неопределенности в значениях экзогенных параметров рассматриваемой модели.
Применение методики на примере определения оптимизированных показателей операционного заказа на размещение и хранение партии грузов в мультимодальной транспортной сети
В качестве примера применения изложенной методики может быть рассмотрена задача определения оптимизированных показателей операционного заказа на размещение и хранение партии грузов в мультимодальной транспортной сети с учетом затрат на содержание запаса на единицу площади или объема склада при следующих характеристиках для нечетко-интервальных экзогенных параметров исследуемой модели:
A1 = 820 (y.e.), A2 = 860 (y.e.),
A3 = 920 (y.e.), A4 = 980 (y.e.),
S1 = 7500 (y.e.), S2 = 7800 (y.e.),
S3 = 8000 (y.e.), S4 = 8350 (y.e.),
a1 = 0,04 (y.e./м2), a2 = 0,06 (y.e./м2),
a3 = 0,08 (y.e./м2), a4 = 0,09 (y.e./м2),
k1 = 0,55 (м2), k2 = 0,60 (м2),
k3 = 0,70 (м2), k4 = 0,73 (м2).
Функция принадлежности для нечетко-множественной характеристики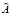 
представлена на рис. 1, нечетко-множественной характеристики 
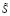представлена на рис. 2, нечетко-множественной характеристики 
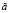представлена на рис. 3, и на рис. 4 представлена функция принадлежности для нечетко-множественной характеристики 
.
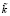Соответствующая приведенным исходным данным функция принадлежности для нечеткого множества, описывающего оптимизированный показатель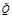 
(ед.) операционного заказа на размещение и хранение транспортной компанией партии грузов с учетом затрат на содержание запаса на единицу площади склада, полученная с применением соотношений (8), представлена на рис. 5.
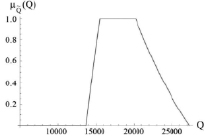
Рис. 5. Функция принадлежности для нечетко-множественной характеристики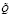 
Заключение
Проведен анализ нечеткой модели оптимизации заказов с учетом затрат на хранение запасов для транспортной компании как логистического посредника и дистрибьютора при учете неопределенности экзогенного параметра затрат компании на хранение запасов. В модели используется специализированная версия соотношения Уилсона, к которому применяется модифицированный эвристический принцип обобщения. При исследовании модели были учтены факторы неопределенности для ее экзогенных параметров. Рассмотрен вариант численной реализации исследуемой нечеткой модели определения оптимизированного размера операционного заказа в мультимодальной транспортной сети с учетом затрат по содержанию запаса на единицу площади или объема склада. Также проведен эксперимент применения методики на примере определения оптимизированных показателей операционного заказа на размещение и хранение партии грузов в мультимодальной транспортной сети.