Одним из направлений модернизации технологического оборудования машиностроительных предприятий Российской Федерации является повышение эффективности выполняемых операций, при снижении габаритных размеров и массы механизмов их приводов [8, 9]. Качество получаемых результатов напрямую зависит от корректности реализации, в соответствии со служебным назначением, законов движения исполнительным органом технологической машины. Обеспечение данного эффекта достигается посредством четкого согласования передаточных отношений всех элементов привода технологического оборудования. Существует большое разнообразие механизмов приводов с промежуточными телами, обеспечивающих реализацию вращательного движения входного звена во вращательное перемещение выходного звена [1–6, 10], которое непосредственно контактирует с исполнительным органом технологической машины. Однако на современном этапе развития технологического оборудования зачастую возникает потребность преобразования вращательного движения входного звена в поступательное перемещение исполнительного органа технологической машины. Это означает, что при определении передаточного отношения механизма привода необходимо обеспечить учет реального взаимодействия его выходного звена с исполнительным органом формируемой технологической машины, что является актуальной задачей, решение которой возможно обеспечить посредством использования эксцентриковых механизмов качения (ЭМК) [8, 9].
ЭМК являются разновидностью семейства механизмов с замкнутой системой тел качения (ЗСТК), позволяющих обеспечить требуемое движение выходного звена при минимально возможном числе подвижных звеньев. Эксцентриковые механизмы качения обладают структурой, образованной совокупностью двух колец с дорожками качения, сепаратора, выполняющего роль водила, и тел качения с диаметрами равной или разной величины, которые могут обладать рабочими поверхностями с выступами (зубчатые) или гладкими поверхностями (фрикционные). Для механизмов данного вида величины характерно наличие нескольких симметричных структурных схем, каждая из которых может реализоваться как с сепаратором, так и при его отсутствии в структуре механизма [8, 9].
Коллектив авторов проводит исследования геометрических, кинематических и силовых параметров механизмов приводов технологического оборудования, разработанных на базе механизмов с ЗСТК и ЭМК. В ходе исследований авторами получены формулы для расчета передаточных отношений планетарных механизмов с ЗСТК для всех видов структурных схем при ведущем, как наружном, так и внутреннем кольце, обеспечивающих преобразование вращательного движения во вращательное движение, а также установлены возможные диапазоны их значений [7–9]. Анализ результатов этих исследований показывает, что они не позволяют получить приемлемое решение задачи по определению передаточного отношения для случая преобразования вращательного движения входного внутреннего кольца эксцентрикового механизма качения в поступательное движение исполнительного органа технологической машины, связанного с выходным звеном ЭМК.
Настоящее исследование проводится с целью разработки алгоритма определения передаточных отношений для случая преобразования вращательного движения входного внутреннего кольца эксцентрикового механизма качения в поступательное движение исполнительного органа технологической машины, связанного с выходным звеном ЭМК. Полученные результаты позволят расширить область применения механизмов данного вида, а также создадут возможность для формирования приводов на их базе для случая поступательного движения исполнительного органа технологической машины.
Методы исследования, применяемые в настоящей работе, основаны на общепринятых положениях теоретической механики и теории механизмов и машин.
Рассмотрим решение поставленной задачи на примере определения передаточных отношений для случая преобразования вращательного движения входного внутреннего кольца эксцентрикового механизма качения в поступательное движение исполнительного органа технологической машины, связанного с выходным звеном ЭМК. Для этого сформируем схему движения звеньев эксцентрикового механизма качения на основе структурной схемы при наличии на оси симметрии максимального и минимального тел качения (рисунок, а), где е – эксцентриситет, rmin, rmax, ri, RВ, RН – радиусы минимального, максимального и i-го тела качения и дорожек качения внутреннего и наружного колец.
Будем считать, что внутреннее кольцо 1 имеет неподвижную геометрическую ось вращения и является ведущим звеном (рисунок, а), а точка ОВ принадлежит оси этого звена, следовательно, также является неподвижной. В этом случае, тела качения 2, обкатываясь по дорожке качения внутреннего кольца без скольжения, будут вынуждены взаимодействовать с дорожкой качения наружного кольца 3 также без скольжения. В то же время наружное кольцо 3, являющееся выходным звеном эксцентрикового механизма качения, соединено с исполнительным органом технологической машины и имеет ограничение от перемещений в окружном направлении относительно своего центра вращения точки ОН. Эта точка имеет возможность совершать переносное движение по окружности радиусом равным величине эксцентриситета е относительно неподвижной точки ОВ, что определяет особенности колебательного движения наружного кольца. Учитывая отмеченные особенности, при помощи общеизвестного в теории механизмов и машин метода планов, выполним синтез плана линейных скоростей (рисунок, б). При синтезе плана скоростей воспользуемся понятием характерных точек, за которые примем точки контакта тел качения с дорожками качения внутреннего и наружного колец механизма, т.е. точки А, С, D, F, а также геометрические центры звеньев ЭМК, соответствующие точкам В, Е, ОВ, ОН и ОS (рисунок).
Анализ схемы движения звеньев эксцентрикового механизма качения (рисунок, а) показывает, что вследствие переносного движения центра вращения наружного кольца точка С, принадлежащая дорожке качения этого кольца, будет линейно перемещаться по оси Y (рисунок, а). Точка С одновременно принадлежит и телу качения 2, контактирующему в точке А с ведущим внутренним кольцом ЭМК.
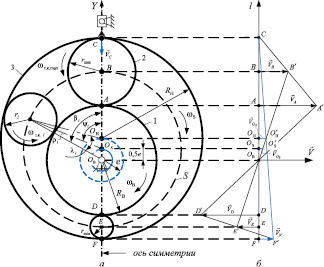
Схема движения звеньев ЭМК (а) и план линейных скоростей (б) при ведущем внутреннем кольце
Определим относительную линейную скорость точки А (рисунок, а), принадлежащей дорожке качения ведущего внутреннего кольца эксцентрикового механизма качения
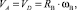(1)
где ωВ – угловая скорость внутреннего кольца.
Точка А также принадлежит максимальному телу качения ЭМК, в этом случае скорость этой точки будет равна
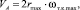(2)
здесь rmax и ωт.к.max – радиус и угловая скорость максимального тела качения.
Приравняв (1) и (2) и выполнив преобразования, получаем выражение для определения угловой скорости максимального тела качения относительно собственного центра вращения
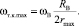
Геометрический центр i-го тела качения не расположен на оси симметрии, следовательно, точки его контакта с дорожками качения смещены на угол клина λi (рисунок, а). Тогда угловая скорость i-го тела качения относительно собственного центра вращения равна
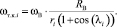(3)
Передаточное отношение от ведущего внутреннего кольца к телу качения определяется соответствующим отношением угловых скоростей этих звеньев. Тогда, учитывая равенство (3), при остановленном наружном кольце, получаем
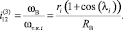(4)
Из прямоугольного треугольника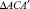 
(рисунок, б) следует, что относительная линейная скорость центра вращения тела качения максимального радиуса (точка B) равна
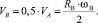(5)
Точка B, так же, принадлежит сепаратору, а её линейная скорость, относительно неподвижного центра вращения ведущего внутреннего кольца, определяется по равенству
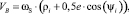(6)
здесь ωS – угловая скорость сепаратора; ρi и ψi – расстояние и угол расположения центра i-го тела качения, рассчитываемые по формулам
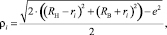(7)
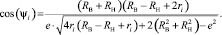(8)
Приравняв (5) и (6), а также проведя соответствующие преобразования, определим угловую скорость сепаратора
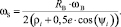(9)
Передаточное отношение от внутреннего кольца к сепаратору, при остановленном наружном кольце, определяется соответствующим отношением угловых скоростей этих звеньев. С учётом (7) и (8), выполним преобразования (9), в результате получим
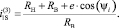(10)
Центр вращения сепаратора (точка ОS) подвижен и совершает переносное движение по окружности с радиусом 0,5е относительно неподвижной точки ОВ (рисунок, а) со скоростью
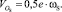(11)
Сепаратор является ведомым звеном, следовательно, его угловая скорость зависит от угловой скорости ведущего внутреннего кольца эксцентрикового механизма качения и изменяется на передаточное отношение. Тогда, с учётом (9) и (10), равенство (11) примет вид
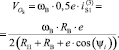(12)
Переносная скорость движения центра вращения наружного кольца (рисунок, б) зависит от линейной скорости центра вращения сепаратора и его угловой скорости относительно центра вращения ведущего внутреннего кольца ЭМК, тогда с учетом (12) будем иметь
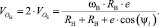
Ранее было установлено, что наличие переносного движения центра вращения наружного кольца обеспечивает перемещение точки С по оси Y (рисунок, а), которое зависит от углового перемещения внутреннего кольца и сепаратора эксцентрикового механизма качения. Следовательно, когда сепаратор повернётся на угол ψi, точка С переместится по оси Y на следующую величину
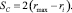(13)
С учётом, что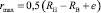 
, равенство (13) примет вид
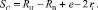(14)
Выполним преобразования (14) с учётом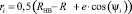 
, получаем зависимость, определяющую линейное перемещение точки С наружного кольца ЭМК
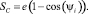(15)
С учётом (8), формула (15) примет вид
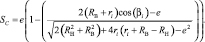
Дифференцируя по времени выражение (15), получаем скорость точки С
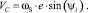(16)
Выполним с учетом (8) и (9) преобразования (16), получаем формулу для линейной скорости точки С в зависимости от угловой скорости ведущего внутреннего кольца ЭМК
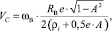(17)
где
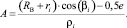
Анализ полученной зависимости (17) показывает, что передаточное отношение от ведущего внутреннего кольца эксцентрикового механизма качения, совершающего окружное вращательное движение, к исполнительному органу технологической машины, связанному с наружным кольцом ЭМК и совершающим линейное перемещение (рисунок, а), равно
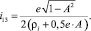(18)
При равенстве нулю величины эксцентриситета, ЭМК преобразуется в схему механизма-прототипа эквивалентную схеме радиального подшипника качения (РПК). Внутреннее и наружное кольца РПК имеют совпадающие геометрические оси и могут совершать только вращательные движения, следовательно, в данном случае передаточное отношение, определяемое по формуле (18), должно равняться нулю. Подставив в равенство (18) условие e = 0, получаем результат равный нулю, что подтверждает достоверность и правильность представленных кинематических зависимостей.
Математические равенства (4), (10) и (18) позволяют определить все виды передаточных отношений эксцентрикового механизма качения при ведущем внутреннем кольце. Анализ этих формул показывает, что для случая переносного движения наружного кольца его точка имеет возможность совершать перемещения по оси Y. Это означает, что наличие связи наружного кольца ЭМК с исполнительным органом технологической машины обеспечивает для него возможность совершения поступательного движения.
Заключение
В результате выполненных исследований получена формула, позволяющая рассчитать передаточное отношение для случая преобразования вращательного движения входного внутреннего кольца эксцентрикового механизма качения в поступательное перемещение исполнительного органа технологической машины, связанного с наружным кольцом ЭМК. Так же установлены равенства для передаточных отношений от ведущего внутреннего кольца эксцентрикового механизма качения к его ведомым звеньям: к телам качения (4) и к сепаратору (10). Это позволяет расширить область применения механизмов данного вида, а также создает возможность для формирования на их базе приводов для случая поступательного движения исполнительного органа технологической машины.