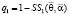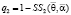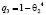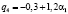Оптимизация процессов управления играет важную роль в решении задач увеличения эффективности работы любой системы. Важной составляющей управления является разработка математических моделей соответствующих процессов, что обычно сводится к определению неизвестных параметров состояния объекта по экспериментальным данным, то есть решается так называемая обратная задача. Линейные обратные задачи были полностью решены с теоретической точки зрения в конце XIX века, из нелинейных до 1970 г. был решён только один класс задач – задача обратного рассеяния, что вызвано их большой сложностью.
В этом плане следует различать две проблемы:
1. Непосредственный подбор аналитических зависимостей по экспериментальным данным в конкретных условиях.
2. Восстановление целостной модели, которая должна удовлетворительно описывать экспериментальные данные в некотором диапазоне внешних параметров.
Первая из указанных задач решается стандартными методами регрессионного анализа, в котором достоверность описания сводится к определению доверительного интервала при определенных допущениях о статистическом характере разброса экспериментальных данных. При таком подборе желательно определить вид аналитической зависимости исходя из смысла задачи (это может быть набор экспонент или набор периодических синусов как в случае задачи колебания и т.п.). Эти методики достаточно хорошо отработаны и имеется большое количество программных продуктов, которые позволяют быстро и эффективно восстанавливать такие аналитические зависимости. В качестве примеров таких пакетов можно привести DataFit, OriginPro, Sigmaplot и т.п. Более универсальные средства решения этой задачи можно найти в общих статистических пакетах типа Statistica или StatGrafics.
Вторая задача, и мы будем говорить в основном о ней, является более сложной. Она характеризуется тем, что вид аналитической зависимости явно не задан, а получается в качестве решения системы дифференциальных уравнений, описывающих модель. В этом случае в систему дифференциальных уравнений обычно входят некоторые параметры процесса (их часто называют кинетическими параметрами), при этом требуется определить их значения, при которых поведение модели удовлетворительно описывает экспериментальные данные в некотором диапазоне внешних условий.
При этом достоверность самой модели зависит как от правильности феноменологического описания, так и от достоверности определения числовых значений параметров модели. В этом случае с экспериментальными данными приходится сопоставлять некоторое решение системы дифференциальных уравнений (обыкновенных или в частных производных). При решении таких задач математическая модель процесса содержит в себе ряд допущений, которые могут существенно повлиять на достоверность окончательных результатов [2].
Плохая обусловленность задач восстановления аналитических зависимостей по экспериментальным данным может быть вызвана различными причинами. Так, для линейных моделей это слишком большое число параметров в многомерной модели, для решения которых используются методы понижения размерности задачи. Для нелинейных моделей, описывающих реальные технические системы, имеется скорее не избыток параметров, а недостаток информации о процессе.
Важно понимать, что плохая обусловленность обратной задачи не является следствием простой небрежности в организации эксперимента или плохой точности измерений. Очень часто объективно невозможно изменять в широких диапазонах некоторые параметры или произвести необходимое число экспериментов (как это часто бывает в медицинских и экономических задачах). Это приводит в итоге к плохо обусловленной задаче при определении параметров процесса. Априорный анализ моделей с целью выявления множественности или мультиколлинеарности решений позволяет подобрать такие поисковые процедуры, которые помогут подобрать оценки параметров с наименьшей дисперсией [3, 5, 6, 8]. Одним из таких подходов, позволяющих уменьшить «плохую обусловленность» задачи, является введение субъективных ограничений, основанных на имеющемся опыте исследователя. При наличии таких ограничений вместо отыскания экстремума функционала, порождаемого методом наименьших квадратов, разыскивается экстремум более общего функционала, в который мера рассогласования входит наряду с дополнительными априорными ограничениями. Введение таких ограничений можно выполнить по методу «теории качеств» Г.И. Брызгалина [4]. Достоверность полученных результатов при таком подходе, конечно, зависит от вводимых экспертных оценок и поэтому требует, как правило, дополнительной проверки. Это не уменьшает ценность предлагаемого подхода, поскольку экспертные оценки достаточно четко сформулированы и могут легко уточняться в процессе работы. В итоге происходит автоматический выбор из серии «плохо обусловленных» решений наиболее правдоподобно описывающих конкретную реальную ситуацию [2].
Теория качеств и ее приложения к параметрической идентификации математических моделей
В общем случае математическую модель объекта или процесса можно представить как систему уравнений вида
Y = F(X, A), (1)
где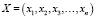 
представляет собой вектор, компонентами которого являются факторы, 
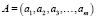– вектор варьируемых параметров системы уравнений, 
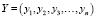– вектор откликов, F – заданная векторная функция. Достаточно часто неизвестным является не только вектор параметров А, но и векторная функция F, т.е. задача построения модели включает в себя 2 этапа:
1) структурная идентификация модели – отыскание вектор-функции F(X, A), принадлежащей заданному классу функций, которая наилучшим образом приближает решение Y экспериментальным точкам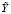 
;
2) параметрическая идентификация – отыскание оптимального значения вектора варьируемых параметров А.
Задача параметрической идентификации моделей относится к классу обратных задач. По определению Адамара такие задачи являются некорректными, что связано с наличием почти линейных зависимостей между факторами. В работе [1] было доказано, что некорректность связана с недостатком информации об описываемом процессе. Этот недостаток может быть восполнен экспертными ограничениями на параметры процесса. При наличии таких ограничений вместо отыскания экстремума функционала, порождаемого методом наименьших квадратов, разыскивается экстремум более общего функционала, в который стандартная мера рассогласования входит наряду с дополнительными априорными ограничениями. Очень часто дополнительная информация о процессе является либо косвенной, либо эмпирической. Следовательно, необходим механизм преобразования такой информации в вид, пригодный для дальнейшей обработки. Для такого преобразования мы предлагаем использовать методы теории качеств.
Основная суть метода заключается в том, что каждому значению каждого свойства или параметра pi ставится в соответствие степень его приемлемости qi, называемая значением частного качества, соответствующего данному свойству. Свойства измеряются каждое в своей шкале, а все частные и единое качество измеряются в общей для всех шкале качеств.
Предположим, что все частные качества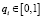 
, где 0 соответственно наихудшее значение, а 1 наиболее приемлемое значение качества. Необходимо построить общее качество системы
q = Q (q1, q2, ..., qn) (2)
с областью определения в n-мерном пространстве качеств.
Для того, чтобы не только все частные, но и единое качество q, вычисляемое по формуле (2), количественно выражало степени приемлемости, имеющие тот же смысл, оно также должно быть представлено в шкале качеств. Если, например, все частные качества равны 1, т.е. соответствуют отличным значениям свойств, то и единое качество, вычисленное по формуле (2), должно быть равно 1, а если все свойства оценены как превосходные, то частные и единое качества также должны превосходить единицу. Такие требования будут обеспечены только при условии, что единое качество подбирается как некое среднее для множества значений частных качеств, иными словами функция в правой части (2) должна принадлежать классу средних функций.
Введем определение: дифференцируемая функция Q(q1, q2,…,qn) называется нормализованной средней, если Q(0, 0,…,0) = 0 и для любого qi выполняются условия:
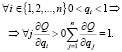(3)
Наиболее интересными нормализованными средними являются средние по Колмогорову – Нагумо [7]:
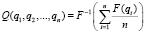, (4)
где F(x) – любая монотонная функция.
Пусть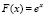 
, тогда
,
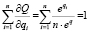так как
.
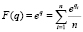Для того чтобы мы могли использовать подобные функции не только для свертки качеств системы в одно общее, но и для составления функционала представляющего собой меру соответствия решения Y экспериментальным точкам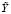 
, необходимо, чтобы при изменении значений частных качеств объекта, единое качество изменялось подобным образом.
Теорема. Если Q(q1, q2,…,qn) – нормализованная средняя функция, то при
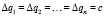
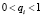
и
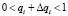
необходимо имеет место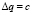 
, где Δq = f(q1 + Δq1, q2 + Δq2,..., qn + Δqn) – f (q1, q2, ..., qn).
Доказательство. По формуле конечных приращений Лагранжа имеем:
,
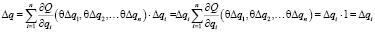что и требовалось доказать.
Единое качество системы определяют из соотношений для функционального среднего (2). В качестве осредняющей функции часто используют либо ln(x), либо ex, что приводит к общей целевой функции в виде
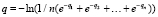(5)
или
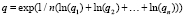. (6)
Выбор этих двух осреднений основан на том, что они обладают большей чувствительностью к изменению частных качеств, чем среднее арифметическое. В зависимости от характера процесса и предъявляемых к нему требований иногда разумно использовать другие осреднения, например, arctg(x), если, в частности, требуется, чтобы значительное увеличение или ухудшение каких-то качеств системы не приводило к существенному изменению общего качества системы.
Пример применения методов теории качества к оценке параметров модели выбора вида транспорта
В качестве примера рассмотрим модель выбора потребителем между двумя видами транспорта. Данная модель предложена Денебургом, де Пальма и Каном (1970 г.). Рассматриваются равноправные пары «исходный пункт – пункт назначения», между которыми должно быть выполнено некоторое число D перевозок.
Пусть x1 – количество перевозок автомобилями, а x2 – автобусами, тогда модель выглядит следующим образом:
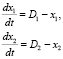
при условии
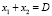. (7)
Пусть A1 и A2 показатели предпочтительности видов транспорта, тогда
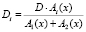. (8)
Определим вид функций А1 и А2. Будем считать, что эти функции зависят не только от скорости транспорта v1 и v2, но и от психологических факторов Fi.
,
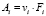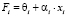, (9)
где θi – влияние рекламы (для автомобилей примем равным 0), αixi – влияние популярности. Для скоростей примем следующие выражения:
,
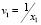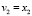, (10)
т.е. при увеличении числа автомобильных перевозок их скорость сокращается в связи с загруженностью автодорог, а скорость автобусных перевозок растет. В конечном итоге модель примет вид:
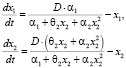
при условии
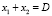. (11)
Неизвестными в данной модели являются константы θ2 и αi. В качестве меры отклонения расчетных значений числа перевозок автомобильным транспортом x1(t) от экспериментальных значений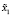 
возьмем функционал порожденный методом наименьших квадратов.
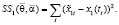(12)
Аналогично можно ввести меру отклонения для числа автобусных перевозок:
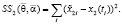(13)
Для численной оценки наличия мультиколлинеарности будем использовать число обусловленности Тодда для информационной матрицы задачи, вида
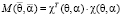, (14)
где
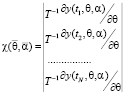, (15)
причем матрица T удовлетворяет соотношению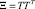 
(
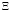– дисперсионная матрица вектора откликов).
Для классической суммы квадратов отклонений (12) или (13) число обусловленности оказывается слишком велико. В точке экстремума (0.89; 0,8; 0,23) P-число = 3,7646×1014, что говорит о наличии существенной мультиколлинеарности.
Частные качества
|
Свойство системы |
Неприемлемые значения |
Приемлемые значения |
Функция частного качества |
|
|
Нормально |
Превосходно |
|||
|
Дисперсия для x1 |
более 1•10–6 |
[1•10–7, 1•10–6] |
менее 1·10-7 |
|
|
Дисперсия для x2 |
более 1•10–6 |
[1•10–7, 1•10–6] |
менее 1·10-7 |
|
|
Влиятельность рекламы автобусов θ2 |
менее 0 и более 1 |
[0, 0,15] и [0,85, 1] |
(0,15; 0,85) |
|
|
Популярность автомобилей α1 |
менее 0,3 и более 1 |
[0,3; 0,7] |
(0,7; 1) |
|
Воспользуемся подходами теории качеств и внесем в модель некоторую дополнительную информацию. Экспертами были выделены следующие свойства системы (таблица), которым впоследствии были сопоставлены функции частного качества.
В качестве осредняющего был выбран функционал вида
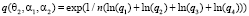. (16)
Оценкой вектора параметров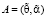 
будем называть такое значение вектора A, что
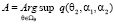. (17)
Экстремум осредняющего функционала достигается в A’(0.89; 0,8; 0,23). Если провести оценку числа обусловленности информационной матрицы порожденной функционалом (16), то окажется, что в окрестностях точки экстремума число обусловленности существенно уменьшилось, P-число = 124. Это позволяет нам говорить о наличии незначительной мультиколлинеарности (или о ее полном отсутствии), что в свою очередь подтверждает хорошее качество построенной модели.
Заключение
Конечно, надо понимать, что достоверность полученных результатов зависит от достоверности тех предположений, которые были сделаны относительно приемлемых диапазонов констант. Другими словами, они зависят от уровня компетенции эксперта, который формулирует эти допущения. Тем не менее при наличии достаточно большого опыта эксперта, опирающегося на широкий спектр имеющихся данных, могут быть получены достоверные данные относительно кинетических констант. Тем более что теория качеств помогает оперативно корректировать вводимую экспертную оценку.