Во время ремонта городских коммунальных сетей (тепловых, водопроводных и т.п.) образуются ремонтные рвы и траншеи на месте городских дорог, что вызывает перекрытие автомобильных дорог на длительное время и необходимость организовывать неудобные для водителей объезды. Это вызывает образование автомобильных пробок, ухудшает транспортную логистику города, увеличивает уровень аварийности и т.п.
В этих условиях, вместо вынужденных путей объездов отрытых коммунальных рвов и траншей, можно организовывать движение по мостовым переездам через них, не перекрывая движения по основным дорожным магистралям города. Для решения данной задачи нами предлагается конструкция мостового переезда – модульный коммунальный путепровод (рис. 1). Путепровод устанавливается через ремонтные рвы коммунальных сетей и позволяет не останавливать транспортные потоки на время ремонта подземных инженерных сетей.
Применение таких мостовых переездов значительно улучшает транспортную логистику в городе во время ремонтных работ на коммунальных сетях: уменьшает образование автомобильных пробок, отсутствуют вынужденные объезды ремонтных участков, что экономит время водителей автомобилей и жителей районов города.
Рис. 1. Модульный коммунальный путепровод
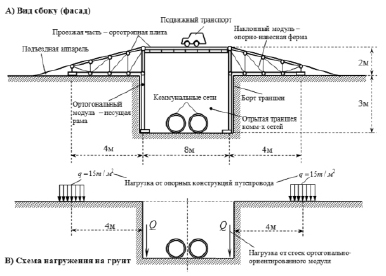
Рис. 2. Схема путепровода и схема нагружения на грунт
Модульный коммунальный путепровод собирается из унифицированных сборно-разборных модулей двух типов: одного ортогонально-ориентированного модуля и двух наклонных модулей (рис. 2).
Ортогонально-ориентированный модуль представляет собой пространственную стальную раму, основание которой крепится на дно ремонтной траншеи специальными способами. Верхняя часть рамы представляет собой проезжую часть в виде ортотропной плиты с подкрепляющими ребрами жесткости.
Наклонный модуль представляет собой стальные фермы, несущие на себе проезжую часть также в виде ортотропной плиты. Консольная часть ферм опирается на грунтовое основание, навесная часть ферм опирается на несущую раму ортогонального модуля.
На место установки мостовой переезд доставляется отдельными модулями и собирается в «однополосном» или «двухполосном» виде методом «сцепки».
Габаритные размеры «однополосных» модулей следующие: длина ортогонально-ориентированного модуля – 8 м; ширина – 3,5 м; высота (с учетом установки их на дно траншей) – 5 м. Длина наклонного модуля – 4 м; ширина – 3,5 м; большая высота – 2 м; меньшая – 0,2 м.
После использования коммунального путепровода производится его разборка по отдельным модулям в узлах «сцепки», а затем они доставляются на места их хранения.
Цель исследования
Сцепление с несущей рамой наклонных модулей позволяет избежать нагрузки на края бортов ремонтных траншей и уменьшает вероятность их обрушения в процессе эксплуатации путепровода. Однако вторые опорные устройства наклонных модулей находятся в силовом взаимодействии с естественным грунтовым основанием. В связи с чем встает задача дополнительного исследования напряженно-деформированного состояния массива грунта и задачи предотвращения обрушения бортов траншей.
Материалы и методы исследования
В результате взаимодействия опорных устройств с естественным грунтовым основанием на участке грунтового массива возникает напряженно-деформированное состояние как в линейно-деформируемой системе. В этом случае с достаточным приближением подобное состояние грунтового массива можно рассматривать как плоскую задачу теории упругости.
Задачу напряженно-деформированного состояния грунта можно решать тремя способами: на основе теории механики грунтов [2, 4–7], численными методами конечных разностей в напряжениях или перемещениях [1, 9]. В данной статье рассмотрим исследование прочности грунтового массива классическими методами механики грунтов.
Результаты исследования и их обсуждение
Расчетная схема участка грунтового массива представлена на рис. 3.
Заменяем действие равномерно-распределенной нагрузки «q» (рис. 2, 3) эквивалентной сосредоточенной силой P = q•(A×B) = 15 т.
Здесь: (A×B) = (1×1) м – размеры опорной части подушки (в плане). Напряжения «σz» вычисляем по формуле [5]:
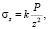(1)
где k = f(r/z) – коэффициент рассеивания (принимается по табл. 1 [8]).
Расчеты по формуле (1) сведены в табл. 1.
Напряжения «σz» можно также вычислить также по формуле (при действии сосредоточенной силы) [4]:
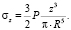(2)
По формуле (2) имеем
Р = 15 т; z0 = 0,5м; y0 = 0; R = z0 = 0,5 м;
;
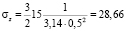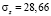(т/м2).
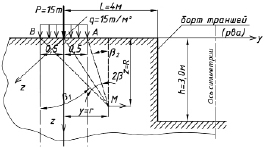
Рис. 3. Расчетная схема нагруженного участка грунтового массива
Таблица 1
Значения «σz»
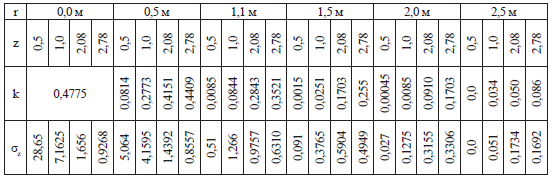
Данное значение совпадает со значениям σz (1-й столбец табл. 1).
На рисунке приведена картина «изобар» при действии сосредоточенной силы для величин σz = 1, 2, 3, 5, 10, 15, 20, 25 (т/м2). При этом использованы выражения
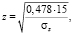
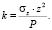(3)
Вычислим нормативное давление на грунт (решение профессора Н.П. Пузыревского) [2]:
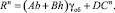(4)
В качестве грунта рассмотрен суглинок (в условиях г. Караганды) со следующими параметрами: Υоб – объемный вес грунта; Сн = 2,1 т/м2 – нормативное удельное сцепление; φ = 15° – нормативный угол внутреннего трения; по [2] А = 0,325; В = 2,30; D = 4,845.
Приняты также:
b = 1,0 м – меньшая сторона опорной подушки (рис. 3);
h = 0,0 м – глубина заложения подошвы опорной подушки.
По формуле (4) имеем
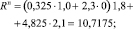
Rн = 10,7175 т/м2 – нормативное давление на грунт, R = Rн•1,2 = 12,861.
Расчетное давление на грунт:
R = 12,861 т/м2. (5)
Напряжения (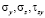
) можно вычислять в долях от нагрузки «Р», т.е. при y0 = 0; z0 = 0,5 м по [4] имеем
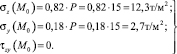(6)
Далее вычисляем главные напряжения [8]:
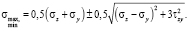(7)
По выражению (7), с учетом значений (6), имеем
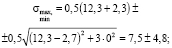
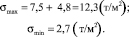
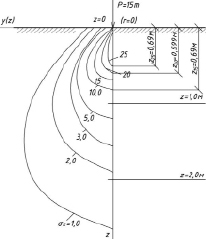
Рис. 4. Изобары напряжений по глубине грунта
Условие прочности грунтового массива имеет вид
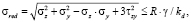(8)
где σred – приведенное напряжение;
R – расчетное сопротивление грунта (выражение (5));
Υ = 0,9 – коэффициент условий работы;
kd = 1,2 – динамический коэффициент.
Приведенное напряжение в грунтовом массиве равно по (8)
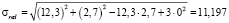т/м2.
σred = 11,197 т/м2. (9)
По (8) с учетом значений (5, 9) получим, что 11,197 < 12,861. Таким образом, условие прочности грунтового массива (8) для нашего случая выполняется.
Рассмотрим вопрос устойчивости участка грунтового массива. Считается, что в линейно-деформируемом грунтовом массиве возникает две системы линий скольжения, наклоненных под углом (45° ± φ/2) (φ – угол внутреннего трения слоя грунта) к направлению (σ1) – большего главного напряжения, т.е. σ1 = σmax. Критической является такая нагрузка, превышение которой приводит к сдвигу в основании по поверхности скольжения, которая охватывает всю подошву опорной подушки (рис. 5) и создает «выпирание» грунта.
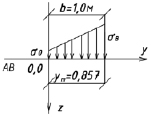
Рис. 5. Зона текучести грунта
Для определения критических нагрузок на грунты оснований составлены таблицы Н.Н. Соколовского [2, 4, 5]. На рис. 5 приведен случай, когда q = 0 (отсутствие пригрузки на поверхности земли). Относительные ординаты предельных давлений даны в табл. 2. Переход от табличных значении к аналитическому выражению производится по формуле [5]
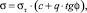, (10)
где c – сила сцепления грунта (т/м2).
Ординаты «y» вычисляют по формуле
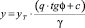, (11)
где γ – объемный вес грунта, т/м3.
Условие устойчивости грунта от выпирания записывается по формуле [3, 10]
k•P < Pпр, (12)
где Р – фактически действующая нагрузка на подошве фундамента (по опорной подушке) т; Рпр – предельно допустимая на грунт сила, т; (k = 2÷3) – коэффициент запаса устойчивости грунта.
Принятый в начале статьи размер в плане опорной подушки (b×b = 1×1 м) обеспечивает достаточную прочность грунтового массива. При расчете на устойчивость грунтового массива размер опорной подушки увеличим до (b×b = 1,2×1,2 м). Проверим выполнения условия (12) для случая (рис. 3): принимаем b = 1,2 м – ширина опорной подушки конструкции; h = 0; q = 0; φ = 150; c = 2,1 т/м2; Υ = 1,8 т/м3.
По табл. 2 (при y = 0): yт = 0, σт = 11 (безразмерная величина). Из формулы (11) (при y = b = 1,2 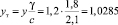м): 
м.
По табл. 2 (yт = 1,0285): σт = 13,874 (безразмерная величина). По формуле (10) определим ординаты эпюры предельных давлений (см. рис. 5):
а) (при y = 0 м): σ0 = σт с = 11·2,1 = 23,1 т/м2;
б) (при y = 1,2 м): σв = σт с = 13,874·2,1 = = 29,1354 т/м2.
Суммарная предельная нагрузка (по эпюре – на рис. 5):
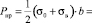
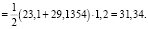
Таким образом
Pпр = 31,34 т. (13)
Таблица 2
Относительные (безразмерные) значения «σт»
|
y φ, град |
0,0 |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
|
5 |
6,5 |
6,7 |
7,0 |
7,2 |
7,4 |
7,6 |
7,8 |
8,0 |
8,2 |
|
10 |
8,3 |
9,0 |
9,6 |
10,2 |
108,0 |
11,3 |
11,8 |
12,3 |
12,8 |
|
15 |
11,0 |
12,5 |
13,8 |
15,1 |
16,2 |
17,3 |
18,4 |
19,4 |
20,5 |
|
20 |
14,8 |
17,9 |
20,6 |
23,1 |
25,4 |
27,7 |
29,8 |
31,9 |
34,0 |
|
25 |
20,7 |
27,0 |
32,3 |
37,3 |
41,9 |
46,4 |
50,8 |
55,0 |
59,2 |
|
30 |
30,1 |
43,0 |
53,9 |
64,0 |
73,6 |
82,9 |
91,8 |
101,0 |
109,0 |
|
35 |
46,1 |
73,8 |
97,1 |
119,0 |
140,0 |
160,0 |
179,0 |
199,0 |
218,0 |
|
40 |
75,3 |
139,0 |
193,0 |
243,0 |
292,0 |
339,0 |
386,0 |
432,0 |
478,0 |
|
y φ, град |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
7,0 |
7,5 |
8,0 |
|
5 |
8,2 |
8,3 |
8,5 |
8,7 |
8,8 |
9,0 |
9,2 |
9,4 |
9,5 |
|
10 |
12,8 |
13,2 |
13,7 |
14,1 |
14,5 |
14,9 |
15,4 |
15,8 |
16,2 |
|
15 |
20,5 |
21,4 |
22,4 |
23,3 |
24,3 |
25,2 |
56,1 |
27,0 |
27,9 |
|
20 |
34,0 |
36,0 |
38,0 |
39,9 |
41,8 |
43,8 |
45,7 |
47,5 |
48,9 |
|
25 |
59,2 |
63,3 |
67,3 |
71,3 |
75,3 |
79,2 |
83,1 |
87,0 |
90,8 |
|
30 |
109,0 |
118,0 |
127,0 |
135,0 |
143,0 |
151,0 |
160 |
168 |
176 |
|
35 |
218,0 |
237,0 |
256,0 |
275,0 |
293,0 |
312,0 |
331 |
349 |
368 |
|
40 |
478,0 |
523,0 |
567,0 |
613,0 |
658,0 |
703,0 |
– |
– |
– |
Проверим условие устойчивости по формуле (12) с учетом значения (13) (Р = 15 т; k = 2):
2•15 < 31,34, т.е. 30 < 31,34.
Таким образом, условие устойчивости выполняется.
Выводы
1. Проведено исследование взаимодействия естественного грунтового основания за пределами отрываемых рвов и траншей подземных инженерных сетей с опорными устройствами наклонных опорно-навесных модулей мостового переезда (рис. 2); при этом произведена оценка прочности и устойчивости указанного участка грунтового массива.
2. Установлено, что при действующей схеме нагружения прочность грунтового массива под опорной подушкой обеспечивается при ее размерах в плане (b×b = 1×1 м). Однако для выполнения условия устойчивости необходимо принять размеры опорной плиты в плане не менее (b×b = 1,2×1,2 м). Таким образом, окончательно принимаются размеры опорной плиты в плане (b×b = 1,2×1,2 м), т.е. наибольший размер из расчетов на устойчивость и прочность.
3. Известные теории механики грунтов применены для расчета исследуемого грунтового массива, рассматриваемого как линейно-деформируемая связанная система.
4. Предлагаемые методики расчетов могут быть применены для подобных систем, состоящих из грунтового массива с различными физико-механическими характеристиками (при разных величинах угла трения, объемной массы, сил сцепления и т.д.).