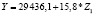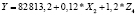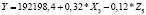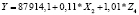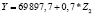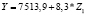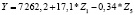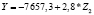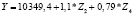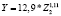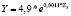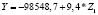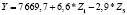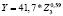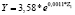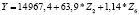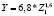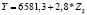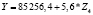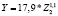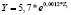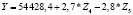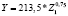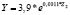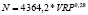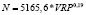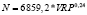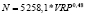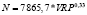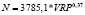Для совершенствования процесса налогового планирования на современном этапе развития экономики большинства стран имеет место необходимость разработки новых методик, основанных на всестороннем учете множества влияющих факторов на величину поступлений налоговых платежей в бюджетную систему различного уровня [1, 4].
Прогнозирование налоговых доходов бюджета должно осуществляться исходя из того, что это сложный и многоэтапный процесс. В этой связи возникает необходимость разработки системы таких мер по решению задач прогнозирования налоговых поступлений, которые позволили бы объективно оценить величину поступлений платежей по каждому налогу на определенный период с учетом наиболее существенных влияющих факторов. Для решения подобных задач актуальным на сегодняшний день является инструментарий эконометрического моделирования. Одним из важнейших инструментов данного метода является корреляционно-регрессионный анализ.
В литературе вопросу применения различных количественных методов в прогнозировании макроэкономических показателей уделяется достаточное внимание [2, 5, 6].
Необходимо также отметить и некоторые авторские работы по этому направлению [3], где построены значимые эконометрические многофакторные модели прогнозирования налоговых поступлений и выявления тенденций развития макроэкономических показателей региона.
В работе нами предпринята попытка построить оригинальные по структуре и составу факторов регрессионные модели прогнозирования объемов поступлений по налогу на доходы физических лиц.
Данные, приведенные в табл. 1, свидетельствуют о том, каково же значение налога на доходы физических лиц в формировании доходной части консолидированных бюджетов регионов РФ в 2015 г. Так, в указанном году доля НДФЛ в общих доходах КБ субъектов РФ составляла 31 %. Если говорить в разрезе федеральных округов, то почти во всех округах его доля составляла свыше 30 %. Данный факт еще раз говорит об актуальности задачи планирования данного налога на основе регрессионных моделей.
Таблица 1
Данные структуры доходов консолидированных бюджетов регионов РФ в 2015 г. (в разрезе некоторых федеральных округов)
|
Федеральный округ/регионы |
Доходы, всего, млн руб. |
Налог на прибыль организаций |
НДФЛ |
Налог на имущество |
Безвозмездные поступления |
Доля НДФЛ в общих доходах |
|
Центральный федеральный округ |
||||||
|
Белгородская область |
81 081,9 |
11 507,1 |
23 738,6 |
12 739,4 |
20 569,1 |
29,3 |
|
Брянская область |
49 827 |
3 118,2 |
11 518,2 |
3 979,1 |
23 700,6 |
23,1 |
|
… |
… |
… |
… |
… |
… |
… |
|
Орловская область |
31 958,5 |
2 822,2 |
8 219,1 |
2 912,9 |
12 109,9 |
25,7 |
|
Рязанская область |
50 598,6 |
7 740,3 |
14 617,8 |
7 185,0 |
11 913,6 |
28,9 |
|
Смоленская область |
38 559,7 |
7 987,0 |
11 624,1 |
4 743,7 |
7 303,5 |
30,1 |
|
Тамбовская область |
48 751,6 |
6 108,7 |
10 819,0 |
4 949,7 |
19 842,6 |
22,2 |
|
Тверская область |
62 121,1 |
10 786,5 |
16920,6 |
9 768,8 |
11 245,3 |
27,2 |
|
Тульская область |
75 423,2 |
16 973,3 |
20191,2 |
7 048,1 |
13 963,0 |
26,8 |
|
Ярославская область |
64 758,4 |
10 288,5 |
18589,1 |
9 918,2 |
8 808,2 |
28,7 |
|
г. Москва |
1 673 525,8 |
484 746,1 |
695 411 |
144 111,1 |
75 323,7 |
41,6 |
|
Итого |
3 090 416,0 |
735 401,7 |
1 114 094 |
343 619,7 |
346 180,5 |
Ср. 28,4 |
|
в % к итогу |
100,0 |
23,8 |
36,0 |
11,1 |
11,2 |
|
|
Северо-Западный федеральный округ |
||||||
|
Республика Карелия |
34 801,5 |
3 114 |
10 131,4 |
3 274,9 |
10 535,8 |
29,1 |
|
Республика Коми |
67 419,7 |
16 371,9 |
21 870,5 |
13 150,2 |
6 649,1 |
32,4 |
|
… |
… |
… |
… |
… |
… |
… |
|
Архангельская область |
78 414,3 |
15 877,2 |
23 195,5 |
7 337,4 |
19 120,8 |
29,6 |
|
Псковская область |
26 843,0 |
2 617,0 |
7 474,8 |
2 262,4 |
9 400,2 |
27,8 |
|
г. Санкт-Петербург |
447 420,2 |
111 528,6 |
181 021,2 |
46 388,9 |
24 073,1 |
40,5 |
|
Ненецкий автономный округ |
18 470,6 |
3 438,8 |
2 422,3 |
4 373 |
904,5 |
13,1 |
|
Итого |
1 019 572,0 |
241 372,7 |
342 693,7 |
123 024,8 |
124 972,2 |
Ср. 28,9 |
|
в % к итогу |
100,0 |
23,7 |
33,6 |
12,1 |
12,3 |
|
|
Южный федеральный округ |
||||||
|
Республика Адыгея |
17 004,7 |
1 424,5 |
3 549,4 |
1 523,9 |
7 112,8 |
20,9 |
|
Республика Калмыкия |
11 257,5 |
471,0 |
1 754,9 |
1 048,4 |
6 112,4 |
15,6 |
|
Краснодарский край |
236 840,6 |
37 244,9 |
73 613,3 |
37 978,3 |
36 907,6 |
31,1 |
|
Астраханская область |
38 627,0 |
7 984,9 |
11 653,5 |
5 514,1 |
7 326,1 |
30,2 |
|
Волгоградская область |
100 282,9 |
19 488,0 |
27 219,1 |
12 330,5 |
22 628,5 |
27,1 |
|
Ростовская область |
170 793,4 |
25 938,8 |
49 720,2 |
22 932,9 |
38 655,5 |
29,1 |
|
Итого |
574 806,1 |
92 552,1 |
167 510,4 |
81 328,1 |
118 742,9 |
Ср. 25,7 |
|
в % к итогу |
100,0 |
16,1 |
29,1 |
14,1 |
20,7 |
|
|
… |
… |
… |
… |
… |
… |
… |
|
РФ, всего, млрд руб. |
9 308,2 |
2 107,6 |
2 807,8 |
1 068,6 |
1 683,0 |
|
|
в % к итогу |
100,0 |
22,6 |
30,2 |
11,5 |
18,1 |
Таким образом, целью нашего исследования является построение регрессионных уравнений (моделей), описывающих зависимость объема налога на доходы физических лиц от различных социально-экономических показателей развития региона, построенных в разрезе федеральных округов.
Корреляционно-регрессионный анализ и построение регрессионных уравнений взаимосвязи налога на доходы физических лиц и показателей развития региона
На первом этапе исследования были выделены различные показатели развития регионов, которые должны в последующем стать основой для построения регрессионных моделей прогнозирования налога на доходы физических лиц. Таковыми факторами являются следующие:
Z1 – среднегодовая численность занятых в экономике, тыс. чел.;
Z2 – среднедушевые денежные доходы населения, руб.;
Z3 – среднемесячная заработная плата, руб.;
Z4 – общая численность населения, тыс.чел.;
Z5 – численность безработного населения, тыс. чел.;
Z6 – средние душевые расходы, тыс. руб.;
Z7 – объем платных услуг, тыс. руб.
На начальном этапе исследования нами применена процедура экспертного оценивания значимости влияния факторов на поступление по налогу на доходы физических лиц. Согласование мнений экспертов было проведено с применением медианы Кемени. Так как факторы для различных регионов (федеральных округов) имеют различное значение, то были привлечены эксперты, представляющие различные субъекты РФ. Для этого была организована сетевая экспертиза.
Далее в исследовании в результате проведенных стандартных процедур корреляционно-регрессионного анализа с применением средств вычислительной техники построены статистически значимые регрессионные уравнения, которые показывают зависимость налога на доходы физических лиц от различных показателей развития регионов в разрезе федеральных округов (табл. 2–12).
Таблица 2
Матрица коэффициентов корреляции (Центральный федеральный округ)
|
Y |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z6 |
Z7 |
|
|
Y |
1 |
|||||||
|
Z1 |
0,84 |
1 |
||||||
|
Z2 |
0,82 |
0,76 |
1 |
|||||
|
Z3 |
0,84 |
0,42 |
0,74 |
1 |
||||
|
Z4 |
0,78 |
0,78 |
0,41 |
0,24 |
1 |
|||
|
Z5 |
0,68 |
– 0,76 |
– 0,32 |
– 0,45 |
0,68 |
1 |
||
|
Z6 |
0,59 |
0,62 |
0,71 |
0,82 |
0,52 |
– 0,71 |
1 |
|
|
Z7 |
0,55 |
0,63 |
0,52 |
0,35 |
0,65 |
– 0,53 |
0,58 |
1 |
Таблица 3
Регрессионные уравнения прогнозирования налога на доходы физических лиц по изменению экономических показателей регионов Центрального федерального округа
|
Вид уравнения |
R2 |
Показатели эластичности, % |
|
|
0,69 |
0,74 |
|
|
0,63 |
Z2 – 0,79, Z4 – 0,68 |
|
|
0,64 |
Z3 – 0,71, Z5 – 1,01 |
|
|
0,68 |
Z2 – 0,94, Z7 – 1,01 |
|
|
0,76 |
1,02 |
На первом этапе подобных процедур нами построена матрица коэффициентов корреляции между социально-экономическими показателями развития регионов Центрального федерального округа за 2015 гг. С ее помощью нами определены показатели, имеющие тесную корреляционную связь (r > 0,7). Они одновременно не будут включены как факторы-аргументы в многофакторные регрессионные уравнения. Также выявлена тесная связь между результативным показателем (Y – поступления налога на доходы физических лиц) и такими макроэкономическими показателями регионов ЦФО, как Z1 (среднегодовая численность занятых в экономике), Z2 (cреднедушевые денежные доходы населения), Z3 (среднемесячная заработная плата), Z4 (общая численность населения).
Для регионов Центрального федерального округа получены различные регрессионные уравнения, по которым можно сделать вывод о зависимости величины поступлений налога на доходы физических лиц от изменения социально-экономических показателей развития регионов. Выявлено, что максимальное значение среднего коэффициента эластичности (0,94) имеет показатель Z2 – cреднедушевые денежные доходы населения. Это говорит о том, что при изменении данного показателя населения на 1 % от своего среднего значения объем поступлений по налогу на доходы физических лиц изменится на 0,94 % от своего среднего значения (табл. 3).
Таблица 4
Матрица коэффициентов корреляции (Северо-западный федеральный округ)
|
Y |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z6 |
Z7 |
|
|
Y |
1 |
|||||||
|
Z1 |
0,81 |
1 |
||||||
|
Z2 |
0,89 |
0,78 |
1 |
|||||
|
Z3 |
0,82 |
0,48 |
0,71 |
1 |
||||
|
Z4 |
0,77 |
0,72 |
0,44 |
0,28 |
1 |
|||
|
Z5 |
0,71 |
– 0,71 |
– 0,38 |
– 0,35 |
0,68 |
1 |
||
|
Z6 |
0,41 |
0,66 |
0,77 |
0,76 |
0,42 |
– 0,77 |
1 |
|
|
Z7 |
0,52 |
0,64 |
0,57 |
0,32 |
0,58 |
– 0,48 |
0,61 |
1 |
Таблица 5
Регрессионные уравнения прогнозирования налога на доходы физических лиц по изменению экономических показателей регионов Северо-Западного федерального округа
|
Вид уравнения |
R2 |
Показатели эластичности, % |
|
|
0,82 |
1,01 |
|
|
0,72 |
Z1 – 0,87, Z5 – 0,98 |
|
|
0,84 |
1,12 |
|
|
0,77 |
Z2 – 1,07, Z5 – 1,28 |
Для регионов Северо-Западного федерального округа получены несколько значимых регрессионных уравнений (однофакторных и многофакторных) линейного вида.
По ним можно сделать вывод о том, как в среднем изменяется величина налоговых поступлений по НДФЛ в зависимости от изменения различных социально-экономических показателей (табл. 5).
Далее для регионов Южного федерального округа также была построена матрица коэффициентов корреляции между макроэкономическими показателями (табл. 6). И на ее основе были сделаны выводы о целесообразности включения в регрессионные уравнения различных факторов, результаты которых приведены в табл. 7.
Таблица 6
Матрица коэффициентов корреляции (Южный федеральный округ)
|
Y |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z6 |
Z7 |
|
|
Y |
1 |
|||||||
|
Z1 |
0,77 |
1 |
||||||
|
Z2 |
0,83 |
0,77 |
1 |
|||||
|
Z3 |
0,76 |
0,48 |
0,75 |
1 |
||||
|
Z4 |
0,41 |
0,72 |
0,33 |
0,32 |
1 |
|||
|
Z5 |
0,70 |
– 0,77 |
– 0,32 |
– 0,37 |
0,66 |
1 |
||
|
Z6 |
0,38 |
0,64 |
0,72 |
0,73 |
0,42 |
– 0,72 |
1 |
|
|
Z7 |
0,43 |
0,68 |
0,57 |
0,32 |
0,58 |
– 0,44 |
0,63 |
1 |
Таблица 7
Регрессионные уравнения прогнозирования налога на доходы физических лиц по изменению экономических показателей регионов Южного федерального округа
|
Вид уравнения |
R2 |
Показатели эластичности, % |
|
|
0,78 |
1,14 |
|
|
0,64 |
1,04 |
|
|
0,75 |
1,3 |
|
|
0,76 |
Z2 – 0,97, Z5 – 1,18 |
По анализу табл. 7 можно отметить следующее. Для регионов Южного федерального округа наиболее значимым фактором (показатель эластичности равен 1,3), имеющим существенное влияние на поступление объема налога на доходы физических лиц, оказался Z1 – среднегодовая численность занятых в экономике. Также на поступление платежей по этому налогу оказывает существенное влияние показатели Z2 – cреднедушевые денежные доходы населения, коэффициент эластичности которого составил 1,14, Z5 – численность безработного населения с коэффициентом эластичности 1,18.
Вообще говоря, коэффициент эластичности исключительно для уравнений степенного вида имеет постоянное значение и равен значению параметра b. В иных уравнениях показатель эластичности зависит от значения аргумента Zi [6]. В связи с этим для расчета коэффициента эластичности необходимо выполнить дополнительные эксперименты. Они рассчитаны в работе для линейной и экспоненциальной функций [5].
Для регионов Северо-Кавказского федерального округа построены регрессионные уравнения, по которым можно сделать вывод о высоком значении эластичности для таких показателей, как среднегодовая численность занятых в экономике (Z1) и среднедушевые расходы (Z6). Например, рост последнего показателя на 1 % приводит к увеличению налога лишь на 1,05 % (табл. 8).
Таблица 8
Регрессионные уравнения прогнозирования налога на доходы физических лиц по изменению показателей регионов Северо-Кавказского федерального округа
|
Вид уравнения |
R2 |
Показатели эластичности, % |
|
|
0,83 |
0,94 |
|
|
0,76 |
1,08 |
|
|
0,66 |
Z2 – 0,92, Z6 – 1,05 |
Далее в работе построены регрессионные уравнения для регионов Приволжского, Дальневосточного и Сибирского федеральных округов (табл. 9–11). Анализируя результаты данного этапа исследования, можно сделать вывод об эластичности налога на доходы физических лиц по таким показателям, как среднегодовая численность занятых в экономике (Z1), численность безработных (Z5) и среднемесячная заработная плата (Z3).
Таблица 9
Регрессионные уравнения прогнозирования налога на доходы физических лиц по изменению экономических показателей регионов Приволжского федерального округа
|
Вид уравнения |
R2 |
Показатели эластичности, % |
|
|
0,87 |
1,6 |
|
|
0,77 |
1,04 |
|
|
0,81 |
0,97 |
Таблица 10
Регрессионные уравнения прогнозирования налога на доходы физических лиц по изменению экономических показателей регионов Сибирского федерального округа
|
Вид уравнения |
R2 |
Показатели эластичности, % |
|
|
0,84 |
1,1 |
|
|
0,77 |
1,12 |
|
|
0,68 |
1,02 |
Таблица 11
Регрессионные уравнения прогнозирования налога на доходы физических лиц по изменению экономических показателей регионов Дальневосточного федерального округа
|
Вид уравнения |
R2 |
Показатели эластичности, % |
|
|
0,86 |
0,75 |
|
|
0,69 |
1,1 |
Последним этапом построения регрессионных уравнений зависимости поступлений по налогу на доходы физических лиц от различных социально-экономических показателей регионов был этап построения регрессионных зависимостей объема налога на доходы физических лиц (N) от величины валового регионального продукта (VRP) регионов в разрезе федеральных округов (табл. 12).
Таблица 12
Регрессионные уравнения прогнозирования объемов поступлений налога на доходы физических лиц по изменению величины валового регионального продукта регионов федеральных округов в 2015 г.
|
Федеральный округ |
Вид уравнения |
Коэффициент детерминации, R2 |
|
Центральный федеральный округ |
|
0,76 |
|
Северо-Западный федеральный округ |
|
0,72 |
|
Южный федеральный округ |
|
0,72 |
|
Северо-Кавказский федеральный округ |
|
0,68 |
|
Уральский федеральный округ |
|
0,67 |
|
Сибирский федеральный округ |
|
0,69 |
Анализ результатов построения регрессионных уравнений, приведенных в табл. 12, позволяет сделать ряд существенных выводов.
Во-первых, все регрессионные уравнения представляют собой зависимости степенного вида, коэффициент эластичности которых (параметр в степени аргумента уравнения) есть величина постоянная.
Во-вторых, объем поступлений налога на доходы физических лиц является неэластичным по показателю валового регионального продукта (VRP), так как коэффициент эластичности оказался меньше 1 для всех уравнений.
В-третьих, наибольшее значение коэффициента эластичности выявлено для регрессионного уравнения, построенного по Северо-Кавказскому федеральному округу (0,48).
Выводы
Построенные в исследовании регрессионные уравнения (модели) являются оригинальными. Это касается как состава факторов, включенных в каждое уравнение, так и структуры уравнений. Применяя данные уравнения, можно проводить прогнозные расчеты по определению величины поступлений налога на доходы физических лиц в зависимости от таких социально-экономических показателей развития региона, как среднегодовая численность занятых в экономике, среднедушевые денежные доходы населения, среднемесячная заработная плата, численность безработного населения, среднедушевые расходы.
Практическую значимость имеют также и уравнения, описывающие зависимость поступлений по налогу на доходы физических лиц от уровня валового регионального продукта регионов. Они построены для шести федеральных округов России и могут быть применены в расчетах по макроэкономическому прогнозированию и планированию налоговых поступлений на уровне субъектов РФ.
Результаты выполненного исследования могут быть использованы в реализации государственной социально-экономической политики в регионах. В частности, рекомендации и выводы, сделанные на основе этих результатов, позволяют повысить объективность прогнозных расчетов налога на доходы физических лиц, стать основой для разработки параметров социально-экономического прогнозирования развития территории.