Многие современные методы цифровой обработки изображений были разработаны на основе ранее созданных методов для обработки речевых, звуковых, сейсмических и гидроакустических сигналов. Немаловажная часть этих методов связана с задачей подавлением шума. Многие из них основаны на представлении сигнала как некой гладкой функции от параметров (это могут быть время, координаты и т.д.), и поэтому обработка может беспрепятственно вестись как в частотной, так и во временной области [1, 12].
Шумоподавление является одной из наиболее актуальных задач в области компьютерного зрения при обработке как отдельных изображений, так и видеопоследовательностей [3]. Появление шума обусловлено следующими факторами:
– техническими характеристиками оборудования для видеосъемки;
– сложными условиями съемки (недостаточным освещением);
– возникновением помех при передаче данных;
– использованием неточных фильтров при выделении сигналов.
Как уже было сказано, видеопоследовательности могут обладать пространственным и временным шумом. Известно, что наиболее негативный вклад в работу систем компьютерного зрения вносит именно пространственный шум, поэтому для подавления шума на видеопоследовательностях применимы методы шумоподавления [9], предназначенные для обработки отдельных цифровых изображений.
Алгоритмы шумоподавления обычно специализируются на подавлении конкретного вида шума, и их задача заключается в улучшении визуального восприятия изображений и повышении качества и скорости работы алгоритмов детектирования объектов интереса на последующих этапах обработки изображений.
Цифровое изображение уже нельзя представить в виде гладкой функции. Это происходит из-за того, что при отображении трех мерных объектов на плоскости неизбежны (в приближении лучевой оптики) разрывы интенсивности на границах объектов. Поэтому представляется важным рассматривать интенсивность изображения лишь как кусочно-непрерывную функцию. Естественно, хотелось бы учесть этот факт при разработке алгоритма подавления шума, так как в противном случае фильтрация будет приводить к размытию границ и, соответственно, к искажению полезного сигнала.
Таким образом, для подавления шума и сведения к минимуму потери информации на изображении необходимо использовать алгоритмы, способные сохранить границы объектов, в том числе и тех, которые по амплитуде соизмеримы с шумом. Далее рассмотрим базовый алгоритм гауссовской фильтрации и анизотропное диффузионное сглаживание [11].
Фильтр Гаусса
Гауссовская фильтрация заключается в свертке изображения со следующей функцией
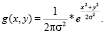
Здесь параметр σ задает степень размытия. Фактически мы имеем линейное усреднение, только пиксель смешивается с другими по закону, заданному функцией Гаусса. Посчитанный по приведенной формуле матричный фильтр называется гауссианом.
Благодаря сепарабельности фильтр Гаусса представим в виде
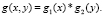
Это означает, что свертку можно производить последовательно по строкам и по столбцам, что позволяет ускорить работу алгоритма при больших размерах фильтра.
Фильтр Гаусса применяется в различных задачах компьютерного зрения, в том числе при детекции объектов дорожной сцены. В частности, в задаче поиска и выделения дорожной разметки (прямых линий) на этапе предварительной обработки [4].
Для некоторых типов помех фильтр Гаусса позволяет достаточно хорошо смазать шумовую компоненту сигнала, при этом размытие границ объектов на изображении происходит в меньшей степени. Это позволяет смазать мелкие детали в кадре, которые не требуют отделения от фона, а крупные объекты сохранить для дальнейшей обработки. Зачастую для локализации границ объектов фильтр Гаусса применяют совместно с градиентными методами. В силу чувствительности градиентных методов к шумам, для смазывания шумовых скачков яркости и, как следствие, исключения порождённых шумом границ предварительно используется фильтр Гаусса.
Кроме того, стоит отметить алгоритмы быстрого рекурсивного вычисления гауссовского фильтра [10].
Анизотропный диффузионный фильтр
Регистрируемое изображение можно рассматривать как сумму идеального изображения и аддитивного шума. Шум является небольшим возмущением на изображении [6]. Наша задача – максимально уменьшить уровень шума при сохранении полезного сигнала.
Диффузия является физическим процессом выравнивания концентрации вещества. Интенсивность сигнала в точке изображения может рассматриваться как «концентрация», а шум как небольшие неоднородности в концентрации. Эти неоднородности могут быть сглажены с помощью диффузии.
Пусть u – распределение концентрации. Тогда закон Фика гласит, что градиенты концентрации вызывают появление потока j, который стремится выровнять концентрации:
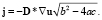
Здесь D – тензор диффузии (в общем случае – положительно определённая симметричная матрица). Таким образом, получается, что тензор диффузии определяет, как соотносятся между собой направления и величины потока диффузии и градиента концентрации. Поэтому в зависимости от поведения тензора выделяют разные типы диффузии:
1. D постоянен вдоль всего изображения: линейная диффузия.
2. D зависит от структуры изображения: нелинейная диффузия.
3. j и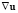 
параллельны: изотропная диффузия.
4. j и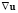 
не параллельны: анизотропная диффузия.
По описанным выше причинам будем рассматривать последний тип диффузии [7]. Для реализации алгоритма нужно вести сглаживание в направлении, перпендикулярном направлению максимальной диффузии, которое в данном случае определяется одним из собственных векторов тензора диффузии. Далее приходим к уравнению диффузии, при решении которого и получается искомый результат – сглаженное изображение, сохраняющее границы.
Локально анизотропный гауссовский фильтр
Главным недостатком ранее рассмотренного алгоритма является его вычислительная трудоёмкость, связанная в первую очередь с необходимостью решать дифференциальное уравнение [5]. В результате решения этой проблемы возник алгоритм анизотропной гауссовской фильтрации.
Изображение рассматривается как кусочно-непрерывная функция f(x, y), разрывы которой соответствуют границам объектов. При подсчёте дисперсии производных можно использовать окна разного типа. Например, квадратное окно [2]. Недостатком этого подхода являются большие скачки тензора при перемещении окна вдоль изображения. Этим недостатком не страдает гауссовское окно, поэтому его мы и будем использовать.
Для определения направления сглаживания будем использовать структурный тензор, определяемый следующим образом:
,
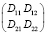где
= 
,
= 
,
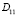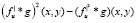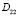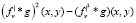D12 = D21 =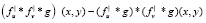 
.
Здесь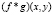 
– свёртка функции f(x, y) с двухмерной гауссианой g(x, y); 
, 
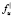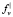– производные по диагоналям. Таким образом Dij – дисперсии производных вдоль диагоналей.
Структурному тензору можно поставить в соответствие эллипсоид. Далее можно определить направление главной оси – оно как раз и будет перпендикулярно границам объектов на картинке. Поэтому нужно вести сглаживание в направлении перпендикулярном направлению главной оси, для того чтобы сглаживать вдоль границ и таким образом избавиться от эффекта размытия.
Свяжем систему координат с пикселом. Тогда угол между направлением главной оси и горизонтальной оси системы координат можно определить по формуле
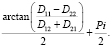
Область значений угла составляет отрезок от 0 до Pi. Эту область можно разбить на 4 части, например так, как показано на рис. 1.
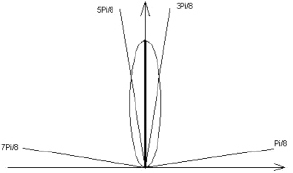
Рис. 1. Разбиение области значений угла между направлением главной оси и горизонтальной осью
В зависимости от того, в какую из областей попадает главная ось эллипса, мы можем определить, в каком из четырех направлений вести сглаживание. Например, на представленном выше рисунке главная ось попала в интервал (3Pi/8, 5Pi/8), поэтому сглаживание имеет смысл вести в перпендикулярном ей направлении, т.е. в направлении горизонтальной оси.
Данный алгоритм работает быстрее анизотропного диффузионного фильтра за счёт того, что в нём нет необходимости решать дифференциальное уравнение, а вместо этого нужно лишь провести свёртку с гауссианой, которая при использовании алгоритма Дерише [8] может быть выполнена за 8 операций на пиксель.
Примеры и результаты
Далее на рис. 2–6 приведены примеры работы предложенного алгоритма на реальных цветных изображениях снежно-ледовой поверхности Арктики, на которых присутствуют основные элементы рельефа (торосы, стамухи, открытая вода, припайный лед). Левая картинка – изначальная, правая – после преобразования.
а) б)
Рис. 2. Снежная поверхность: а) исходное изображение, б) после преобразования
а) б)
Рис. 3. Стамуха, ледовый покров: а) исходное изображение, б) после преобразования
а) б)
Рис. 4. Снежный покров и открытая вода: а) исходное изображение, б) после преобразования
а) б)
Рис. 5. Торосы: а) исходное изображение, б) после преобразования
а) б)
Рис. 6. Припайный лед: а) исходное изображение, б) после преобразования
Обсуждение результатов
В настоящей работе для уменьшения влияния аддитивного шума предложен алгоритм предварительной обработки изображений на основе локально анизотропной гауссовской фильтрации. Результаты обработки изображений арктической поверхности показывают, что предложенный подход имеет близкое с методом анизотропной диффузионной фильтрации визуальное восприятие изображений в части обработки однородных областей и сохранения границ, но при этом обеспечивается высокое быстродействие.
Как следствие, предложенный метод может эффективно применяться не только при обработке отдельных изображений, но и для шумоподавления при обработке видеопоследовательностей в системах компьютерного зрения, работающих в реальном времени.
Работа проводилась при поддержке грантов РФФИ № 15-29-06091 (офи_м) и 15-29-06080 (офи_м).