Дефектом в программном обеспечении принято называть несоответствие ПО установленным или предполагаемым требованиям. Примерами дефектов ПО могут служить неверно рассчитанные платежи по кредитам, сбои в работе карточного процессинга в часы пиковой нагрузки, некорректная тарификация абонентов оператора сотовой связи. Одной из основных задач в тестировании и обеспечении качества ПО является работа с дефектами на всех этапах жизненного цикла: анализ и локализация, описание, проверка исправления. Особо сложной представляется задача анализа плавающих дефектов. Особенность данных дефектов заключается в том, что они воспроизводятся лишь с определенной частотой. Иными словами, отсутствует однозначный сценарий, который приводил бы к проявлению ошибки в 100 % случаев.
Работа с плавающими дефектами является одной из наиболее неразработанных проблем в современной литературе по тестированию и обеспечению качества. Также в существующих на данный момент инструментальных средствах тестирования отсутствует функциональность для работы с данным видом дефектов.
Проблема плавающих дефектов подробно рассматривается в работе [2]: дано определение плавающих дефектов, приведена их классификация, рассмотрены основные особенности и риски, связанные с управлением данными дефектами.
Также в работе [2] предлагается решение следующих задач:
- Грамотное описание дефекта.
- Оценка критичности.
Для решения данных задач был использован аппарат теории вероятностей и математической статистики.
Настоящая статья является продолжением работы [2]. Цель статьи – разработка двух математических моделей для локализации плавающего дефекта. Актуальность статьи объясняется тем, что локализация любого дефекта является первым этапом в процессе его исправления.
Перейдём к рассмотрению первой модели.
Предположим, имеется некоторый внешний фактор, который может находиться только в одном из двух различных состояний. Требуется проверить предположение о том, что данный фактор оказывает влияние на вероятность проявления дефекта.
Пусть р1 – вероятность проявления дефекта при состоянии 1 внешнего фактора, а р2 – вероятность проявления дефекта, когда данный фактор находится в состоянии 2.
Проверяется гипотеза H0, утверждающая, что вероятности проявления дефекта не отличаются в зависимости от рассматриваемого фактора.
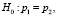
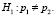
Для проверки данной гипотезы осуществим несколько попыток воспроизвести дефект при каждом из двух состояний внешнего фактора.
Введём следующие обозначения:
- 
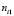– количество раз, когда дефект воспроизвёлся при состоянии i фактора (i = 1, 2);
- 
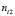– количество раз, когда дефект не воспроизвёлся при состоянии i фактора (i = 1, 2);
- 
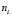– общее число испытаний при состоянии i фактора (i = 1, 2);
- 
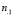– общее число испытаний, в которых дефект проявился;
- 
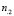– общее число испытаний, в которых дефект не проявился;
- 
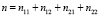– общее число испытаний.
Результаты экспериментов удобно представить в виде таблицы сопряженности (табл. 1).
Таблица 1
Общий вид таблицы сопряжённости для анализа плавающего дефекта
|
Дефект проявился |
Дефект не проявился |
Сумма |
|
|
Фактор в состоянии 1 |
n11 |
n12 |
n1. |
|
Фактор в состоянии 2 |
n21 |
n22 |
n2. |
|
Сумма |
n.1 |
n.2 |
|
|
Общая сумма |
n |
||
Для тестирования гипотезы о равенстве p1 = p2 можно воспользоваться критерием хи-квадрат [1]. Данный статистический критерий можно использовать при выполнении условий
n > 20, (1)
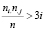, j = 1, 2. (2)
Расчётное значение критерия имеет следующий вид:
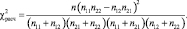(3)
При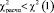 
гипотеза H0 согласуется с результатами наблюдений на уровне значимости α;
При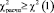 
гипотеза H0 отклоняется.
В данных формулах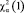 
– это критическая точка распределения хи-квадрат, где α – уровень значимости.
В качестве примера рассмотрим тестирование автоматизированной системы для оценки кредитных рисков. Периодически при попытке загрузки данных о клиентах из смежной MDM-системы (masterdatamanagement) возникает сбой. Система оценки рисков и MDM-система интегрированы через ESB (enterpriseservicebus). За месяц до обнаружения дефекта была произведена миграция на новую систему MDM, разработанную другим вендором. Проверим предположение о влиянии системы MDM на плавающий дефект. Для этого совершим 50 попыток воспроизвести дефект, затем осуществим переключение на старую MDM и совершим ещё 50 попыток. Результаты эксперимента зафиксируем в табл. 2.
Таблица 2
Статистика проявления дефекта в рамках примера с системой оценки кредитных рисков
|
Дефект проявился |
Дефект не проявился |
Сумма |
|
|
MDM система (новая) |
12 |
38 |
50 |
|
MDM система (нецелевая) |
7 |
43 |
50 |
|
Сумма |
19 |
81 |
|
|
Общая сумма |
100 |
||
Проверим условия (1) и (2).
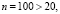
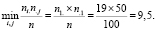
Следовательно, для проверки гипотезы можно воспользоваться критерием хи-квадрат.
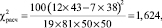
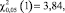
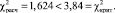
Из последнего неравенства следует, что гипотеза H0 принимается. Это означает, что миграция данных о клиентах в новую MDM не оказывает значимого влияния на проявление плавающего дефекта. Дефект, вероятнее всего, относится к системе оценки рисков либо к ESB.
Продемонстрируем решение данной задачи в R при помощи расчета p-значения. Выполним следующий скрипт R [6]:
defects<- matrix(c(12, 38, 7, 43), nrow = 2, byrow = TRUE)
chisq.test(defects, correct=FALSE) # тест хи-квадрат
В результате исполнения скрипта будут получены следующие результаты (рис. 1).
X_test_statistic<-chisq.test(defects)$statistic # 1. Вычислениерасчетногозначения
X_critical_value<- qchisq(0.05,1, lower.tail=FALSE)# 2. Вычислениекритическогозначения
x=seq(0,6,by=0.01)# 3. Построение графика плотности распределения
y1=dchisq(x, 1, ncp = 0, log = FALSE)
plot(x,y1,type="l",xlab="x",ylab="p(x)",ylim=c(0,1), las=1, bty="n", axes = FALSE)
axis(1, pos=0)# 4. ПостроениеосиOX
axis(2, pos=0, las=1)# 5. ПостроениеосиOY
S<- seq(from = X_critical_value, to = 6, by = 0.001)# 6. Заливкакритической области
x <- c(X_critical_value, S, 6)
y <- c(0, dchisq(S, 1, ncp = 0, log = FALSE), 0)
polygon(x, y, col = "grey", lty = 1, border = "black")
points(X_test_statistic,0, pch=19) # 7. Отметим на графике расчетное значение
text(X_test_statistic, 0, "x^2расч", pos=3)
points(X_critical_value,0, pch=19) # 8. Отметим на графике критическое значение
text(X_critical_value, 0, "x^2крит", pos=3, offset=0.7)
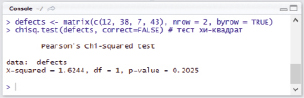
Рис. 1. Результаты исполнения скрипта теста хи-квадрат в среде RStudio
Данные результаты необходимо интерпретировать следующим образом:
- X-squared – это величина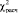 
, рассчитанная по формуле (3);
- p-value – это вероятность того, что случайная величина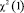 
окажется больше либо равна 
.
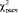Поскольку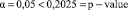 
, то гипотеза H0 принимается.
Проиллюстрируем тестирование гипотезы графически, выполнив следующий скрипт [6]:
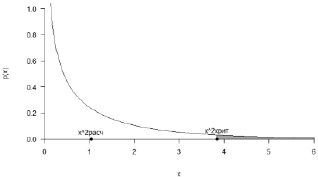
Рис. 2. График плотности вероятности χ2(1) с закрашенной критической областью, с отмеченными на графике расчётным и критическим значениями
В основе второй модели, разработанной в рамках данной статьи, лежит аппарат одномерного дисперсионного анализа (ANOVA).
Рассмотрим внешний фактор, который может находиться в одном из различных состояний. Обозначим через mi – среднее число по попыток до воспроизведения дефекта при i состоянии фактора, i = 1, 2,…,l.
Требуется проверить следующую гипотезу:
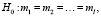
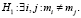
Для проверки гипотезы H0 осуществим nk испытаний для каждого из возможных состояний k = 1, 2…l фактора. Результат каждого испытания – число попыток до проявления дефекта.
Введём следующие обозначения:
- nk – число наблюдений при состоянии k фактора;
- 
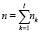– общее число наблюдений.
Доказано [4], что:
,
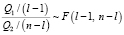где
- 
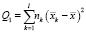– сумма квадратов отклонений выборочных средних 
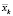от общего среднего 
;
- 
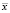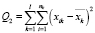– сумма квадратов отклонений наблюдений от выборочных средних групп (внутри групп);
- 
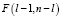– распределение Фишера с l – 1 и n – l степенями свободы.
Расчётное значение может быть рассчитано по следующей формуле:
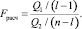(4)
Если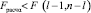 
, то гипотеза H0 не противоречит результатам наблюдений и принимается.
Если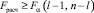 
, то гипотеза H0 отклоняется, и следует считать, что среди значений 
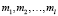имеется хотя бы два не равных друг другу.
В формулах выше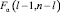 
– критическая точка распределения Фишера с l – 1 и n – l степенями свободы при уровне значимости α.
Вернёмся к примеру с риск-системой. Проверим предположение, что на вероятность проявления дефекта оказывает влияние нагрузка на систему (табл. 3).
Таблица 3
Статистика проявления дефекта в зависимости от уровня нагрузки
|
Число попыток до проявления дефекта |
|||||||
|
Уровень нагрузки 1 |
4 |
2 |
3 |
5 |
5 |
3 |
n1 = 6 |
|
Уровень нагрузки 2 |
6 |
5 |
4 |
7 |
6 |
8 |
n2 = 6 |
|
Уровень нагрузки 3 |
7 |
9 |
8 |
7 |
8 |
6 |
n3 = 6 |
|
Уровень нагрузки 4 |
1 |
7 |
3 |
8 |
5 |
7 |
n4 = 6 |
|
n = 24 |
|||||||
Осуществим необходимые расчёты для проверки гипотезы H0:
l = 4,
l – 1 = 3,
n – l = 20,
Q1 = 46,17,
Q2 = 59,67,
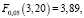
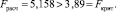
H0 в нашем случае отклоняется и принимается гипотеза H1. Можно сделать вывод о значимо различных результатах испытаний при различных уровнях нагрузки. Это означает, что нагрузка на систему оказывает влияние на вероятность проявления дефекта.
Выполним следующий скрипт в R [5]:
Level1<-c(4,2,3,5,5,3) # вектор данных для уровня нагрузки 1
Level2<-c(6,5,4,7,6,8) # вектор данных для уровня нагрузки 2
Level3<-c(7,9,8,7,8,6) # вектор данных для уровня нагрузки 3
Level4<-c(1,7,3,8,5,7) # вектор данных для уровня нагрузки 4
# F-тест
Combined_Groups<-data.frame(cbind(Level1, Level2, Level3, Level4))
Stacked_Groups<-stack(Combined_Groups)
Anova_Results<-aov(values ~ ind, data = Stacked_Groups)
summary(Anova_Results)
Будут получены следующие результаты (рис. 3).
Построим график плотности распределения F(2,15):
F_test_statistic<- 5.158# 1. Вычисление расчетного значения
F_critical_value<-qf(0.05, 3, 20, lower.tail = FALSE, log.p = FALSE) # 2. Вычисление критического значения
x=seq(0,7,by=0.01)# 3. Построение графика плотности распределения
y1=df(x, 3, 20, log = FALSE)
plot(x,y1,type="l",xlab="x",ylab="p(x)",ylim=c(0,0.8), las=1, bty="n", axes = FALSE)
axis(1, pos=0) # 4. Построение оси OX
axis(2, pos=0, las=1) # 5. Построение оси OY
S<- seq(from = F_critical_value, to = 6, by = 0.001) # 6. Заливка критической области
x <- c(F_critical_value, S, 6)
y <- c(0, df(S, 3, 20, log = FALSE), 0)
polygon(x, y, col = "grey", lty = 1, border = "black")
points(F_test_statistic,0, pch=19) # 7. Отметим на графике расчетное значение
text(F_test_statistic, 0, "Fрасч", pos=3)
points(F_critical_value,0, pch=19) # 8. Отметим на графике критическое значение
text(F_critical_value, 0, "Fкрит", pos=3, offset=1.3)
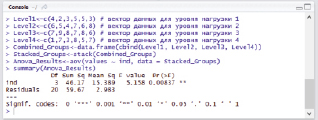
Рис. 3. Результаты выполнения скрипта для тестирования гипотезы в среде RStudio
Интерпретация результатов выполнения скрипта:
- Fvalue – величина Fрасч, вычисленная по формуле (4).
- Pr(> F) – это вероятность того, что случайная величина F окажется больше либо равна Fрасч.
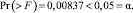
Снова получаем, что принимается гипотеза H1.
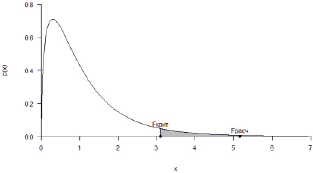
Рис. 4. Плотность распределения F(2,15)с закрашенной критической областью, с отмеченными на графике расчётным и критическим значениями
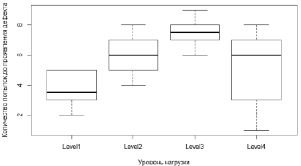
Рис. 5. Диаграмма размаха в рамках примера с уровнями нагрузки
Выполним следующий скрипт R для построения диаграммы размаха, чтобы показать неоднородность наблюдений при разных уровнях нагрузки:
boxplot(values ~ ind, data = Stacked_Groups, xlab="Уровень нагрузки", ylab="Количество попыток до проявления дефекта")
Таким образом, разработаны два инструментальных средства на языке программирования R, которые могут быть использованы для локализации плавающих дефектов в цепочке из нескольких автоматизированных систем либо в отдельной системе.
Данные инструментальные средства могут быть использованы в практической деятельности разработчиков и специалистов по тестированию, а также в учебной деятельности. Внедрение данных средств можно рассматривать как этап оптимизации процессов тестирования с использованием методологии TPINext [3] (рассмотренные в статье модели и инструментальные средства соответствуют десятой ключевой области TPINext – «Управление дефектами»).