Современный уровень развития информационных технологий делает актуальным их использование для экспертной поддержки принятия решений в ситуационных центрах социально-экономического развития, используемых при анализе состояния, динамики развития, логистики территорий различного масштаба (стран, регионов, муниципальных образований и т.п.), производственных комплексов (предприятий, отраслей, направлений экономической деятельности региона и т.п.), оценке эффективности проектов. Это, в свою очередь, требует разработки автоматизированного программного инструментария, адекватного с точки зрения баланса объема и скорости обработки информации социально-экономического характера. К такому инструментарию следует отнести математические модели социально-экономических систем (предприятий, территориальных кластеров, регионов, отраслей и т.п.), алгоритмы расчета показателей и оценки эффективности их функционирования, автоматизированные программные средства финансового, логистического, маркетингового анализа для принятия обоснованных управленческих решений, примеры применения которого приведены в работах [1, 2, 4–7]. Применение соответствующих алгоритмов обработки данных, анализа информации позволяет успешно применять описанный инструментарий при анализе ряда проектов в ситуационном центре социально-экономического развития Кемеровского филиала Российского экономического университета имени Г.В. Плеханова.
Отметим, что, кроме оптимизационных математических моделей социально-экономических систем и соответствующих программных комплексов их анализа, в ситуационном центре используется программное обеспечение многопараметрического анализа математических функций, свойства которого подробно описаны в [3]. В настоящей работе представлены примеры применения указанного программного обеспечения при решении как оптимизационных, так и неоптимизационных задач экспресс-оценки эффективности инвестиционных проектов (ИП), линейной оптимизации, логистики и др.
Пусть требуется оперативно оценить эффективность инвестиционного проекта по критерию чистой приведенной стоимости (NPV). Простейшая формула для расчета NPV, предполагающая инвестиционные затраты лишь в начальный момент времени, имеет вид
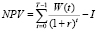 , (1)
, (1)
где W(t) – прибыль предприятия в период (t; t + 1), T – горизонт планирования ИП, I – суммарные инвестиции в проект, r – ставка дисконтирования, учитывающая риски инфляции и требования инвестора. В предположении, что W(t) = W = const (t = 0,1,…,T), которое является целесообразным при экспресс-анализе инвестиционных проектов, применяя формулу аннуитетных платежей, можно получить следующее выражение для NPV:
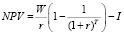 . (2)
. (2)
Рассмотрим полученную формулу, как функцию одной независимой переменной Т с параметрами W, I, r. Записав (2) в легко осваиваемой пользователем математической нотации пакета, описанного в [3], как функцию сначала переменной Т, а затем переменной r, с учетом экономического смысла параметров W, I, r, Т, можно проанализировать поведение (2) в любом, допустимом по смыслу, диапазоне указанных параметров: W денежных единиц (д.е.) – без ограничений, I (д.е.)≥ 0, r ( %) ≥ 0, T(лет) ≥ 0.
На рис. 1–2 представлены зависимости (2) от горизонта планирования и ставки дисконтирования ИП при некоторых значениях параметров W, I, которые, с использованием возможностей пакета, можно оперативно менять в режиме реального времени, с любым шагом. Из получаемых графиков (при изменении любого параметра они перестраиваются практически мгновенно), по рис. 1 аналитик может оперативно оценить период окупаемости РР, NPV и срок ее насыщения, а по рис. 2 – внутреннюю норму доходности IRR инвестиционного проекта, в соответствие с теорией благосостояния. Использование пакета многопараметрического анализа функций позволяет осуществлять эффективный (в смысле целевых установок функционирования ситуационных центров) экспресс-анализ инвестиционных проектов.
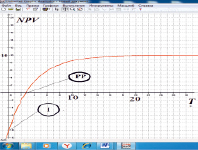
Рис. 1. NPV = NPV(T)
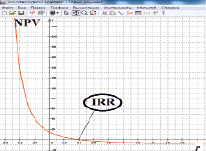
Рис. 2. NPV = NPV(r)
Рассмотрим следующую задачу, ориентированную на экспресс-анализ некоторых инвестиционных и бизнес-проектов мезоэкономического уровня. Известно, что спрос Q и цена P на продукцию являются основными регуляторами отношений между производителем и потребителем в рыночной экономике. Естественным является предположение, что спрос определяется не ценой P на единицу товара и суммарными доходами D потребителя, а относительной покупательской способностью потребителя, то есть отношением доходов к цене. Иначе говоря, если доход потребителя и цена товара увеличатся (уменьшатся) в одно и то же число раз, то спрос останется неизменным. Кроме того, в соответствии с теорией благосостояния А.С. Пигу, спрос обладает свойством насыщения с ростом доходов и постепенным удовлетворением потребности в товаре. Поэтому зависимость суммарного спроса всех работников региона от отношения цены на продукцию к доходам потребителя может быть описана, например, логистической кривой вида
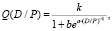 (3)
(3)
где k, b, a – некоторые постоянные величины. Для применения на практике хорошо разработанных методов решения задач линейного (дробно-линейного) программирования, функцию (3), при достаточно реалистичном для региональной экономики условии P<<D, целесообразно представить, как дробно-линейную функцию относительно D/P в виде
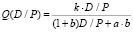 . (4)
. (4)
Построение и сравнительное исследование функций вида (3) и (4) является затруднительным без наличия соответствующих автоматизированных средств. Осуществим подбор параметров a, b, k функций (3) и (4) с использованием пакета, описанного в [3]. Результат численного эксперимента приведен на рис. 3.
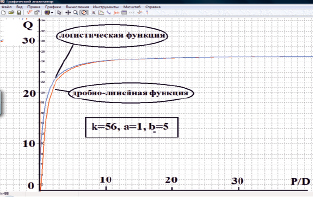
Рис. 3. Графики логистической кривой и дробно-линейной функции (k = 56, b = 1, a = 5)
Как видно из рис. 3, найдена такая числовая комбинация параметров a = 5, b = 1, k = 56, при которой наблюдается теоретически предсказанное хорошее приближение логистической кривой и дробно-линейной функции практически на всей положительной части оси абсцисс. Получить подобный результат аналитическими способами, в короткое время, без применения средств автоматизации расчетов, не представляется возможным.
В экономических приложениях часто используется задача оптимизации значений линейной целевой функции при линейных ограничениях, формирующих непустую область допустимых решений, имеющая следующую содержательную постановку. Пусть n – количество видов производимой в экономической системе продукции; m – количество используемых при производстве продукции ресурсов; i – номер вида ресурса (i = 1, 2,.... m); j – номер вида продукции (j = 1,2,....n); bi – наличный объем i-го ресурса; aij – количество единиц i-го ресурса, затрачиваемого на производство единицы j-й продукции; cj – эффективность (стоимость) единицы продукции j-го вида; xj – искомый объем производства j-й продукции. Тогда задачу максимизации эффекта (прибыли) от производства продукции можно поставить в виде требования максимизации функции
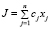 (5)
(5)
при выполнении ограничений неотрицательности переменных xj ≥ 0, j = 1,…,n и использования ресурсов:
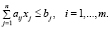 (6)
(6)
Модель (5), (6) справедлива для любого количества видов ресурсов и продукции, для самых разнообразных конкретных численных значений лимитов ресурсов bi и норм затрат ресурсов aij. Очевидно, что при наличии большого количества параметров ее эффективный анализ требует автоматизации обработки информации. Пакет, описанный в [3], справляется с такой обработкой в частном случае задачи (5), (6), когда n = 2, m ≥ 3.
На рис. 4 приведен результат одного численного эксперимента с произвольными значениями параметров в (5), (6). Здесь представлена область 0ABCD допустимых решений, сформированная ограничениями (6). Точка оптимума (например, точка С на рис. 4), а также ее координаты получаются средствами пакета, описанного в [3], (путем изменения параметров, соответствующих значениям коэффициентов с1, с2 и искусственно задаваемому свободному коэффициенту, визуализирующих поворот и параллельное перемещение), как последняя общая точка допустимой области и линии целевой функции (5). Аналогичная визуализация достигается при управлении любым из параметров функций задачи (5)–(7). Это позволяет оперативно изменяя допустимую область и перемещая целевую функцию, решать самые разнообразные задачи как учебного, так и практического содержания.
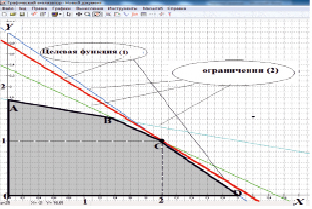
Рис. 4. Пример анализа задачи линейного программирования
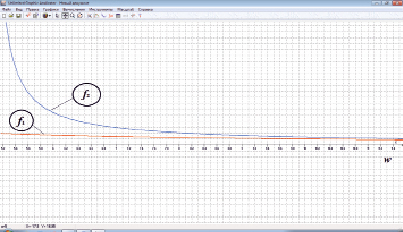
Рис. 5. Графики затрат времени движения объектов (a = b = 5, λ = 0,5)
Рассмотрим еще одну задачу практического содержания. Пусть необходимо доставить товар из пункта А в пункт В через промежуточный пункт С: AC/CB = λ. У принимающего решение лица есть два альтернативных варианта: 1) доставка товара со средней скоростью v по железной дороге, проложенной между А и В; 2) товар доставляется автомобилем со средней скоростью v-a из А в С, а затем из C в В самолетом, со средней скоростью v + b. Необходимо определить значения пропорции λ и параметров а и b, чтобы 2-й вариант доставки оказался быстрее по времени. Полный параметрический анализ приведенной задачи в общей постановке дает следующее решение: равенство соответствующих времен наблюдается, если
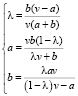 . (7)
. (7)
Очевидно, что пакет, описанный в [3], идеально подходит для визуального анализа полученного решения. Рассмотрим одну из разновидностей сформулированной задачи, имеющую экономически содержательную трактовку и, на первый взгляд, парадоксальное решение. Пусть у производственного предприятия имеется возможность извлечь из некоторого бизнеса потенциал W д.е. путем реализации двух альтернативных сценариев: 1) при условии равномерных усилий w д.е. в единицу времени (ед. вр.) и 2) при условии, что половину потенциала оно будет извлекать с уменьшенными (увеличенными) на а д.е./ед.вр. усилиями, а вторую половину – соответственно с увеличенными (уменьшенными) на ту же величину а усилиями. Требуется ответить на вопрос, какой из вариантов приведет к скорейшему достижению потенциала W. Сформулированная задача может быть легко решена аналитически, но допускает и оперативный ответ на вопрос с использованием пакета, описанного в [3]. С этой целью достаточно построить и сравнить визуально две функции: f1(w) = W/w и f2(w) = 0,5W/(w – а) + 0,5W/(w + а) (рис. 5).
Из полученных графиков быстро убеждаемся, что для всех значений параметров w и а f1(w) < f2(w), что, очевидно, свидетельствует в пользу равномерных усилий предприятия для достижения своего потенциала.
Приведенные результаты свидетельствуют о возможности применения пакета, описанного в [3], в условиях семинаров, мобильных заседаний экспертных групп, ситуационных центров социально-экономического развития за счет скорости обработки информации, простоты использования конечными пользователями, что превращает описанный инструментарий, по сути, в систему поддержки принятия управленческих решений в сфере анализа социально-экономических систем.



