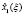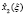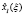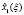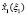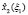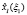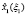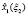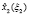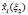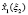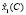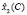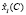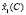Неисправности, возникшие в процессе эксплуатации сложных технических систем, должны быть устранены в кратчайшие сроки в установленном руководящими документами порядке. Такое требование обусловлено тем, что задержки в выполнении работ могут привести к существенным финансовым и репутационным потерям. Кроме того, в процессе поиска причин отказа расходуется как ресурс самого отказавшего изделия, так и потребляемые им электроэнергия, сжатые газы, рабочие жидкости и т.д. [1].
Вместе с тем при выполнении работ по поиску и устранению неисправности должна обеспечиваться безопасность для личного состава, не нанесение ущерба расположенному рядом оборудованию и окружающей среде. В связи с этим данный процесс должен быть четко организован, а личный состав должен уметь оперативно обнаружить причину неисправности.
Весьма важным аспектом при решении задачи повышения готовности персонала указанных систем к оперативной локализации и устранению отказов являются затраты, необходимые для реализации соответствующих мероприятий. В современных условиях актуальной является задача их рационального распределения, решение которой направлено на обеспечение максимально возможной готовности персонала к решению задач по предназначению для заданного объема финансирования.
Таким образом, можно говорить о задаче нахождения оптимального состава мероприятий и соответствующего им объема затрат, при котором рациональное распределение средств на их реализацию позволяет достичь максимальной готовности персонала при заданном объеме финансирования С.
Постановка задачи
Содержательно задачу нахождения оптимального состава мероприятий подготовки персонала к решению целевых задач можно сформулировать следующим образом.
При заданных параметрах организации технологических операций (ТхОп), характеристиках условий функционирования и применения исследуемой системы, характеристиках и параметрах системы обучения найти такой план формирования навыков локализации неисправностей оборудования, который максимизирует показатель эффективности выполнения ТхОп.
Под планом процесса обучения будем понимать вектор, компонентами которого являются длительности обучения персонала соответствующих эксплуатационных подразделений действиям при возникновении отказа оборудования.
Введем следующие обозначения:
Рвз – показатель эффективности выполнения ТхОп;
I – совокупность комплексов аппаратуры (приемно-измерительная аппаратура, аппаратура обработки и выдачи информации, аппаратура энергоснабжения и вентиляции и т.д.);
Ji – множество нештатных ситуаций (вариантов отказов оборудования), навыки локализации которых необходимо сформировать у персонала i-го комплекса аппаратуры;
Тв = {tв ijk} – текущие значения среднего времени локализации неисправности и замены отказавшего элемента;
C – располагаемое количество материальных ресурсов.
Формальная постановка задачи формирования оптимальной программы повышения готовности персонала к решению целевых задач в этом случае примет следующий вид.
Найти:
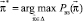 , (1)
, (1)
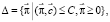 (2)
(2)
где
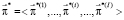 , (3)
, (3)
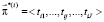 , (4)
, (4)
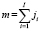 . (5)
. (5)
Длительности tij являются оптимизируемыми переменными и определяют на основе соотношений (3) и (4) векторы 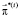 (планы процесса обучения), размерности которых равны числу m возможных нештатных ситуаций при выполнении персоналом задач эксплуатации i-го комплекса аппаратуры. Размерности векторов
(планы процесса обучения), размерности которых равны числу m возможных нештатных ситуаций при выполнении персоналом задач эксплуатации i-го комплекса аппаратуры. Размерности векторов 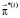 определяются в соответствии с (5).
определяются в соответствии с (5).
Решение данной задачи требует знания зависимостей исследуемого показателя эффективности ТхОп от длительности подготовки персонала. Проанализируем их.
Модели зависимости показателя эффективности ТхОп от времени подготовки персонала
В основу кибернетического подхода к исследованию процесса обучения положено представление обучения как систематического изменения деятельности (или поведения) обучаемого при повторении одинаковой ситуации. Иными словами, обучение предполагает изменение внешней (физической) и внутренней (психической) деятельности обучаемого в соответствии с целью этой деятельности, что приводит, в свою очередь, к улучшению в ходе обучения некоторого показателя, с помощью которого (которых) оценивается достигнутый уровень обученности.
В качестве основной результативной характеристики процесса обучения обычно принимается критерий уровня обученности. При обучении реальных систем в качестве критерия уровня обученности могут выступать следующие характеристики:
- временные (время выполнения действия, операции, время реакции, время, затрачиваемое на исправление ошибки, и т.д.);
- скоростные (производительность труда, скорость реакции, движения и т.д. – величины, обратные времени);
- точностные (величина ошибки в мерах физических величин (миллиметрах, углах и т.п.), количество ошибок, вероятность ошибки, вероятность точной реакции, действия и т.д.);
- информационные (объем заучиваемого материала, перерабатываемой информации, объем восприятия и т.д.).
Под математической моделью обучения будем понимать функциональные зависимости
W = W(tоб), (6)
или
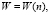 (7)
(7)
где W – некоторый показатель обученности (например, время восстановления, время поиска неисправности, время принятия решения и т.п.);
tоб – время, затраченное на обучение;
n – число циклов (сеансов) обучения.
С помощью зависимостей (6) и (7) необходимо с достаточной степенью адекватности представить в формализованном виде тот процесс, который происходит в обучаемом в результате восприятия им обучающей информации (ОИ).
В соответствии с [2, 3], процесс обучения можно представить в следующем обобщенном виде:
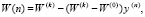 (8)
(8)
где 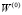 – начальное значение показателя W;
– начальное значение показателя W;
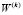 – предельно возможное (конечное) значение показателя W;
– предельно возможное (конечное) значение показателя W;
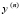 – некоторая монотонно убывающая функция.
– некоторая монотонно убывающая функция.
К виду (8) могут быть преобразованы самые различные модели, как рекуррентной структуры, так и целостно описывающие изменение в процессе показателей обученности (как убывающих, так и возрастающих с увеличением номера цикла обучения).
Таким образом, можно утверждать, что в основе моделирования процесса обучения лежит следующая общая закономерность: в процессе обучения уменьшается по некоторому нелинейному закону остаточная необученность операторов (разность между предельно возможным уровнем и достигнутым уровнем обученности).
В формальном виде данная закономерность представляется выражением (8).
Многочисленные экспериментальные данные свидетельствуют, что важнейшей общей закономерностью итеративного научения является замедленно-асимптотический характер кривых научения. При этом в большинстве случаев [3] кривые итеративного научения аппроксимируются экспоненциальными кривыми (рисунок).
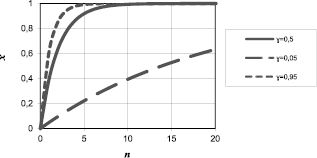
Экспоненциальная модель при различных γ
Сформулированные утверждения вполне согласованы с соответствующими экспериментальными закономерностями, физическими законами и результатами наблюдений.
В этом случае кривая обученности, применительно к процессу обучения персонала, примет вид
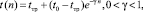
где tтр – требуемое среднее время локализации отказавшего элемента и восстановления оборудования;
t(n) – фактическое время восстановления оборудования после обучения;
n – число циклов обучения.
Метод решения задачи
Полученные выше зависимости показателя эффективности ТхОп от продолжительности подготовки персонала позволяют представить целевую функцию в следующем виде:
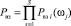 , (9)
, (9)
где ωs – число циклов подготовки персонала i-го подразделения действиям в ситуации j.
Анализ полученных выше зависимостей показывает, что задача синтеза оптимального плана является задачей математического программирования с нелинейной целевой функцией и линейными ограничениями. При этом целевая функция определена в многомерном пространстве, не имеет явного аналитического выражения и определяется рекуррентно. Приведенные обстоятельства существенно усложняют решение задачи.
С учетом того, что функция (9) является сепарабельной, для решения оптимизационной задачи может быть использован аппарат динамического программирования, если производить оптимизацию по одному показателю, а другой представить в виде ограничения [4]. Тогда исходная задача с l неизвестными сводится к последовательному решению l задач с одной неизвестной переменной. При этом находится спектр решений для различных допустимых значений финансирования мероприятий формирования требуемых навыков персонала.
Используя известный [5] алгоритм, приведем решение задачи (9) в терминах динамического программирования.
Функциональное уравнение Беллмана для первого шага условной оптимизации примет вид
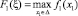 ;
;
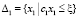 ;
;
Для последующих шагов:
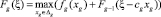 ;
;
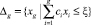 .
.
Для каждого шага, определяющего точность решения задачи, вычисляются максимальные значения функции приращения целевого показателя 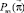 и соответствующие им условно-оптимальные значения каждой переменной
и соответствующие им условно-оптимальные значения каждой переменной 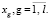 В общем виде результат прямого хода алгоритма динамического программирования представлен в таблице.
В общем виде результат прямого хода алгоритма динамического программирования представлен в таблице.
Результаты выполнения прямого хода алгоритма динамического программирования
|
ξ |
F1(ξ) |
|
F2(ξ) |
|
|
Fl(ξ) |
|
|
|
ξ1 |
F1(ξ1) |
|
F2(ξ1) |
|
|
Fl(ξ1) |
|
|
|
ξ2 |
F1(ξ2) |
|
F2(ξ2) |
|
|
Fl(ξ2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
F1(C) |
|
F2(ξ1) |
|
|
Fl(C) |
|
|
Оптимальные значения каждой переменной при заданном финансировании 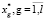 определяются в результате обратного хода алгоритма в соответствии с выражениями
определяются в результате обратного хода алгоритма в соответствии с выражениями
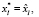
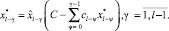
Выводы
В качестве вывода подчеркнем, что практическая реализация предложенного подхода позволит повысить обоснованность рекомендаций по повышению готовности обслуживающего персонала сложных технических систем к возникновению отказов и использованию средств, выделяемых на эти цели.
Кроме того, предложенный подход позволяет получить спектр решений для различных допустимых значений затрат на подготовку персонала соответствующего профиля (от 0 до С с некоторым шагом Δс, определяющим точность решения задачи).