Общеизвестным является факт, что логистические издержки составляют значительную долю добавленной стоимости конечного продукта. Предприятия стараются снизить свои издержки и повысить эффективность операционной деятельности [3, c. 11].
С другой стороны, в процессе развития бизнес претерпел множество изменений, а бизнес-процессы стали более сложными. Исключением не стала и логистическая структура предприятий. В связи с этим не теряет актуальности поиск решения задачи снижения общих логистических издержек предприятия с учетом происходящих в нем изменений [2, c. 8].
1. Предприятие розничной торговли
Рассмотрим предприятие розничной торговли в структуре, в которого присутствуют:
- Поставщики. Доставка грузов поставщиков на склады предприятия осуществляется за счет поставщика и включена в стоимость заказа.
- Склады. Склады имеют зону приемки, зону хранения, зону комплектации и зону отгрузки. При этом товарный ассортимент на складах может отличаться. Склады могут как принадлежать предприятию, так и арендоваться в крупных логистических центрах.
- Транспорт. Доставка на магазины предприятия осуществляется транспортными средствами – грузовыми автомобилями. Рассматриваемое предприятие осуществляет доставку как средствами собственного грузового автопарка, так и посредством аутсорсинга. Грузоподъемность и грузовместимость используемых транспортных средств различается как в собственном автопарке, так и в автопарке подрядчиков [6, с. 17–18].
- Подрядчики. Для доставки товаров на магазин предприятие может пользоваться услугами нескольких подрядчиков [7, c. 35–40].
- Магазины. Предприятие осуществляет торговлю посредством большого количества магазинов. Формат магазинов может различаться, что означает наличие различий в ассортименте представленных в нем товарных позиций.
- Потребители. С точки зрения логистической сети, разумеется, потребители не участвуют в процессах снабжения, приемки, хранения и распределения товаров, однако они формируют спрос, который обуславливает заказы магазинов на доставку товаров и, естественно, количество этих товаров.
Приблизительная схема рассматриваемого предприятия представлена на рис. 1.
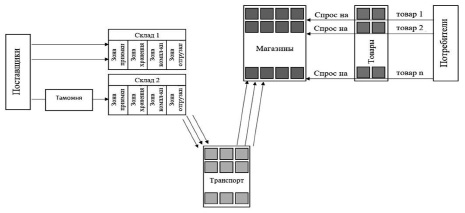
Рис. 1. Схема розничного предприятия
Логистика рассматриваемого розничного предприятия включает в себя следующие сегменты логистической деятельности:
- Логистика снабжения
? Складская логистика
- Транспортная логистика
2. Парадигмы логистики
Общеизвестно, что развитие логистики сопровождалось сменой парадигм, первой из которых была функциональная парадигма. В её рамках оптимизация затрат на логистику была локальной. К примеру, поиск наилучшего объема запасов склада проводился без учета ценовой политики поставщиков и параметров используемого транспорта. Математический аппарат применяемый для решения рассматриваемых в рамках данной парадигмы задач, задач по сути изолированных, стал классикой.
Для решения задач транспортной логистики применялись:
– Задача коммивояжера, для оптимизации маршрутов доставки грузов.
– Транспортная задача, для оптимизации набора доставок покупателю.
Для решения задач складской логистики применялись:
– Задача управления запасами.
– Теория массового обслуживания.
С середины 1980-х гг. в мире утвердилась идея, толчок которой дали работы Майкла Портера: целостное рассмотрение и оптимизация цепей деятельности (цепей создания ценностей) на практике приводит к лучшим результатам, чем изолированная оптимизация таких областей, как снабжение, производство, хранение, распределение [1, c. 43].
На смену функциональной парадигме пришла ресурсная. В рамках данной парадигмы логистическая система рассматривается с точки зрения принципа общих затрат. Иными словами, в рамках одной логистической цепи происходит поиск компромиссов в части затрат. Период распространения ресурсной парадигмы логистики в мире охватывает 1980–2000-е гг., продолжаясь во многих странах и организациях бизнеса и по настоящее время [1, c. 33].
Инновационная парадигма логистики стала дальнейшим логическим продолжением ее эволюции в разрезе передовой концепции Supply Chain Management (Управление цепями поставок) [8, c. 10].
С точки зрения математических моделей и методов, используемых для решения задач оптимизации, переход к данной парадигме означает, что оптимизация практических задач будет в большей части проводиться посредством компьютерных ресурсов. Для поиска оптимальных решений в ЭВМ на вход требуется подать 3 элемента:
- критерии;
- алгоритм;
- входные данные.
Естественно, что общая задача является многокритериальной и получить решение, оптимальное по всем критериям, можно далеко не всегда, потому что критерии зачастую находятся в обратной зависимости. Для решения таких задач уже разработаны методы, которые либо сводят задачу к задаче с одним критерием, либо решаются методами, не использующими этот прием. Ввиду общеизвестности данных методов в рамках данной статьи они рассматриваться не будут.
Любая математическая модель может быть представлена в виде алгоритма. Однако обратное утверждение неверно. В связи с этим модель минимизации общих логистических издержек, как правило, может и не быть поставлена в виде задачи математического программирования.
Третьим элементом, необходимым для решения исходной задачи, являются входные данные, которые обуславливаются рассматриваемой моделью предприятия, а также детализацией изучаемого набора факторов, влияющих на суммарные логистические издержки компании.
3. Критерии
Первым, но далеко не единственным критерием оптимизации логистики розничного предприятия, естественно, можно назвать минимизацию операционных издержек. Исходя из классификации логистики предприятия по сегментам получим следующую целевую функцию:
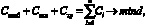 (1)
(1)
где Ci – логистические издержки вида i.
Однако данный вид детализации издержек нельзя назвать подробным. В частности, транспортная логистика решает вопросы связанные с организацией доставки товаров и других материальных ценностей из пункта отправки в пункт назначения. В связи с этим в ведение транспортной логистики попадает задача оптимизации маршрутов доставки товара, загрузки транспортного средства (далее ТС), определения склада отправителя для магазина
В условиях рассматриваемой подзадачи поиска оптимального набора маршрутов перевозки суммарные затраты можно детализировать до уровня одного рейса, как это представлено в модели ниже:
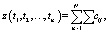 (2)
(2)
где 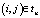 , а N – количество маршрутов в наборе, которое заранее не известно.
, а N – количество маршрутов в наборе, которое заранее не известно.
Интерес представляет не только поиск минимального значения издержек, но и сам набор маршрутов:
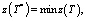 (3)
(3)
где 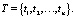
В более детализированном виде целевую функцию общей задачи можно записать в следующем виде:
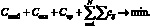 (4)
(4)
Как уже отмечалось нами ранее, оптимизация может производиться по нескольким параметрам, и вторым критерием оптимальности логистики предприятия является уровень сервиса. В него входят:
- время доставки;
- качество поставки (минимальный риск недопоставки и прочих отклонений от плана).
Соответствие времени доставки товара планируемому времени, а также величина отклонения одного значения от другого также является критерием качества сервиса логистической службы предприятия, при условии неизменности качества товара.
Под качеством доставки понимается целостность груза и осуществление самого факта доставки [4, c. 3–8]. Автомобиль, к примеру, может сломаться и не доставить товар в магазин.
4. Доказательство
С точки зрения минимизации общих затрат привлекательной выглядит идея минимизации компонентов эти затраты составляющих. Однако даже в условиях одного критерия – минимизации издержек данный подход не сможет гарантировать результат.
Для этого рассмотрим следующую логистическую задачу. Имеется торговая сеть, состоящая из 9 магазинов, 2 складов и 2 грузовых автомобилей. Каждый автомобиль обслуживает свой склад и, соответственно, один находится на складе А, другой на складе Б. На рис. 2 изображена схема расположения магазинов и складов.
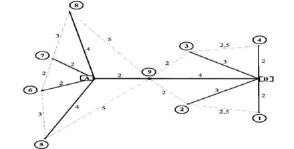
Рис. 2. Схема расположения складов и магазинов рассматриваемой логистической задачи
Решение задачи состоит в том, чтобы составить оптимальный план доставки и маршрут перевозок товаров со складов в магазины. Для простоты задачи принимается однородность грузов и равенство потребностей магазинов в товаре. Найдем оптимальный план перевозок.
В табл. 1 представлена стоимость в тыс. рублей перевозки 100 единиц груза с соответствующих складов в определенные магазины. Также для простоты в условие задачи входит и тот факт, что грузоподъемность имеющихся в распоряжении грузовых автомобилей – 1000 единиц однородного товара.
Таблица 1
Таблица стоимостей перевозок грузов, потребности магазинов и запасы складов рассматриваемой логистической задачи
|
Магазины |
||||||||||
|
Склады |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Запасы |
|
А |
6,5 |
3,5 |
4 |
6 |
4 |
2 |
2 |
4 |
2 |
700 |
|
В |
2 |
3 |
3 |
2 |
8,5 |
8 |
7,5 |
8 |
4 |
700 |
|
Потребность |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
|
Решая данную задачу, получаем следующий результат. Магазины с 1-го по 4-й должны получить свои заказы со склада В, все остальные со склада А.
Затем необходимо определить оптимальные маршруты развоза товаров. Для решения получаем две задачи коммивояжера. Первая, для склада В, имеет в условии следующую матрицу расстояний, представленную в табл. 2.
При решении данной задачи получаем гамильтонов цикл (В; 1) (1; 2) (2; 3) (3; 4) (4; В) [5, c. 232–233]. Издержки данного маршрута составляют по условию задачи 12 тыс. руб. [9 c. 753]. Условие второй задачи представлено в табл. 3.
Таблица 2
Матрица стоимостей перевозок между складом В и магазинами 1–4, тыс. руб.
|
В |
1 |
2 |
3 |
4 |
|
|
В |
М |
2 |
3 |
3 |
2 |
|
1 |
2 |
М |
2,5 |
4,5 |
4 |
|
2 |
3 |
2,5 |
М |
3 |
3,5 |
|
3 |
3 |
4,5 |
3 |
М |
2,5 |
|
4 |
2 |
4 |
3,5 |
2,5 |
М |
Таблица 3
Матрица стоимостей перевозок между складом А и магазинами 5–9, тыс. руб.
|
А |
5 |
6 |
7 |
8 |
9 |
|
|
А |
М |
4 |
2 |
2 |
4 |
2 |
|
5 |
4 |
М |
3 |
4 |
7,5 |
5 |
|
6 |
2 |
3 |
М |
2 |
5 |
4 |
|
7 |
2 |
4 |
2 |
М |
3 |
3,5 |
|
8 |
4 |
7,5 |
5 |
3 |
М |
5 |
|
9 |
2 |
5 |
4 |
3,5 |
5 |
М |
При решении второй задачи получаем гамильтонов цикл (А; 5) (5; 6) (6; 7) (7; 8) (8; 9) (9; В). Издержки данного маршрута составляют по условию задачи 19 тыс. руб. В решении данной задачи есть и другой гамильтонов цикл, однако на результате это никак не сказывается.
Подведем итоги. В результате решения общей задачи путем решения двух оптимизационных задач как части исходной мы получили издержки равные 31 тыс. руб.
Рассмотрим частный случай развоза грузов в исходной задаче. Пусть автомобиль со склада В развезет груз по магазинам в следующей последовательности: (В; 1) (1; 2) (2; 9) (9; 3) (3; 4) (4; В). Со склада А другой автомобиль осуществит развоз товара по маршруту: (А; 5) (5; 6) (6; 7) (7; 8) (8; А).
В результате суммарные издержки в рассмотренном частном случае получаются равными 13+16 = 29 тыс. руб.
Полученный результат является доказательством того, что сумма двух оптимальных решений частей исходной задачи не является оптимальным решением всей задачи.
Из вышеизложенного необходимо сделать вывод, что актуальной представляется разработка методов оптимизации комплексной логистической задачи, состоящей в минимизации затрат на транспортировку и хранение с учетом внешних для логистической системы факторов, а также набора критериев для определения оптимальности полученного решения.
5. Входные данные
Отметить, что на оптимальное решение влияет множество факторов, таких как: модельный ряд собственного автопарка (расход топлива, стоимость ремонта, вероятность поломки), ставки по привлеченным наемным ТС, пробки, ремонт дорог, график работы магазинов, скоростные ограничения, ограничения на въезд на определенные территории ТС определенной тонажности, и другие.
Немаловажным является тот факт, что транспортные средства, участвующие в транспортировке, должны быть оптимальным образом заполнены товаром исходя из следующих параметров:
- грузоподъемность ТС;
- кубатура ТС;
- время разгрузки ТС.
В данном случае последний параметр находится в некоем конфликте с первыми двумя. Дело в том, что многие торговые сети на практике заполняют паллеты, к примеру, на которых осуществляется доставка на магазин, исходя из заказа магазина не полностью. Соответственно с учетом принадлежности паллето-места исключительно к одному заказу возникает пустое пространство в кузове грузового автомобиля.
Формулировка поставленной в статье задачи общей оптимизации логистики может быть использована для разработки методов и алгоритмов, а также непосредственно решения обозначенной проблемы. Для дальнейшей разработки проблематики и решения поставленной задачи планируется использование имитационного моделирования и средств машинного обучения.



