Решать задачу распознавания отдельных рукописных символов существенно проще, чем решать аналогичную задачу распознавания для символов, которые являются частью рукописного текста [3]. В таком случае необходимо не только решать задачу оптического распознавания рукописных символов, но и задачу сегментации рукописного текста – выделения из него отдельных символов и соединяющих их элементов.
Процесс сегментации осложняется характерными для многих почерков искажениями начертаний символов при соединении их графического представления с последующим и предыдущим символами [5].
Цель и задачи исследования
Целью исследования является разработка алгоритма сегментации рукописного текста, который не использует признаковых классификаторов, а также обладает высоким быстродействием и низким потреблением оперативной памяти.
Входными данными для разработанного алгоритма должны являться изображения с начертаниями слов, а выходными – данные, позволяющие однозначно определить способ разбиения пикселей изображения на сегменты, каждый из которых соответствует отдельному символу.
Анализ требований к алгоритму сегментации начертания рукописного слова
Для выполнения сегментации рукописного текста необходимо проанализировать исходное начертание символа, определив принадлежность каждой из областей графического представления участка рукописного текста к определенному символу. Рассмотреть все возможные распределения областей графического представления участка рукописного символа не представляется возможным ввиду огромного количества различных распределений даже для растрового представления начертания [4].
Рассмотренный ранее алгоритм построения структурной модели начертания отдельного символа можно применить для построения структурной модели начертания целого слова [2]. Как и в случае с отдельными символами, в данном случае необходимо предварительно выполнить скелетизацию исходного начертания символа.
В ходе работы алгоритма будет выполнено выделение структурных составляющих, в том числе ключевых точек и изгибов, от местоположения которых можно отталкиваться при выборе границ, разделяющих области начертания последовательных символов сегментируемого текста.
Если рассмотреть примеры структурных моделей отдельных слов рукописного текста, то можно выделить несколько визуальных особенностей этих моделей.
В первую очередь стоит отметить, что большинство разделительных линий между соседними буквами слова можно провести через середину соединяющего ребра. Причем любым из концов такого ребра может быть как ключевая точка, так и изгиб. На рис. 1 можно увидеть случаи, когда оба конца являются ключевой точкой, а также случай, когда один из концов является изгибом.

Рис. 1. Один из вариантов сегментации участка слова
Существуют и изображения, для которых возможен вариант сегментации, при котором разделительная линия может быть проведена через ключевые точки или изгибы. Такое возможно в случаях, когда при начертании отсутствует необходимость в использовании соединительных элементов (рис. 2).
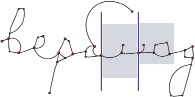
Рис. 2. Сегментация слова с разделительными линиями, проходящими через ключевые точки
Анализ структурных моделей отдельных слов рукописного текста показал, что точками интереса являются ключевые точки, изгибы, а также середины соединяющих их ребер.
Не всегда возможно разделить соседние символы только вертикальными линиями. Иногда графическое представление одного символа может частично находиться над или под графическим представлением соседнего ему символа (рис. 3).
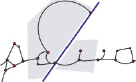
Рис. 3. Пример необходимости в использовании невертикальной разделительной линии
Такие случаи возможны не только из-за особенностей графического представления отдельных символов, но и по причине особенностей почерка, связанных с большей степенью наклона букв.
По результатам перечисленных наблюдений можно сформулировать список требований к алгоритму сегментации рукописного текста: возможность учитывать присутствие на изображении соединительных элементов между соседними символами; возможность отнесения отдельных участков соединительных элементов к начертанию соединяемых символов; использование невертикальных прямых в качестве разделяющих соседние символы линий; учет возможного различия наклона начертаний различных символов в одном слове.
Предложенный алгоритм сегментации изображения рукописного слова
Как было ранее отмечено, точками интереса для выбора местоположений границ между соседними символами слова являются ключевые точки, изгибы и центры соединяющих ребер. Однако задать разделяющую прямую, проходящую через некоторую точку интереса, можно, лишь выбрав вторую точку.
Для решения задачи сегментации было сделано предположение о том, что выбор второй точки можно осуществить так же из множества точек интереса. Процесс построения множества прямых, подмножество которых в итоге станет разделяющими линиями, можно представить в виде перебора всех возможных точек интереса и перебора в пару каждой из них точки для проведения прямой. Для определенности можно полагать, что изначально перебирается нижняя из двух точек, а любая рассмотренная прямая будет впоследствии задаваться вектором из нижней точки в верхнюю. При таком подходе каждая прямая разделяет плоскость структурной модели на две полуплоскости: левую и правую. По большей части элементы структурной модели, принадлежащие правой полуплоскости, относятся к части слова справа от разделительной линии, а оставшиеся, соответственно, – к левой от разделительной линии части. Стоит отметить, что далее будут сделаны уточнения, почему не все точки полуплоскостей могут быть отнесены к соответствующим частям.
Несложно заметить, что в результате работы описанного ранее перебора будет получено O(K2) прямых, которые могут являться разделяющими линиями при сегментации, где K – количество точек интереса в структурной модели. Быстродействие любого алгоритма сегментации, опирающегося на данное множество прямых, так или иначе, будет зависеть от размера этого множества. Следовательно, имеет смысл отсеять как можно больше заведомо некорректных прямых, которые не могут являться разделительными линиями.
Анализ имеющихся структурных моделей рукописных слов позволил выявить три типа прямых, которые можно не рассматривать в качестве возможных соединяющих линий: горизонтальные или близкие к горизонтальным прямые; прямые, которые образованы вектором, пересекающим хотя бы одно соединяющее ребро ровно в одной точке; прямые, пересекающие более двух соединяющих ребер.
Далее для выбранной прямой следует сформулировать четкий принцип, по которому следует определять принадлежность каждого из элементов структурной модели к левой или правой от данной прямой части этой модели. Для этого следует опираться не только на геометрические характеристики прямой, но и на местоположение концов вектора, которым задается эта прямая. Как уже ранее было сказано, задающий прямую вектор направлен снизу вверх. В таком случае мы можем четко определить два значения y1 и y2 координаты на вертикальной оси Y, между которыми находится вектор. Если значение y-координаты ключевой точки или изгиба находится между значениями y1 и y2, то ее принадлежность к левой или правой от разделительной линии части определяется тем, слева или справа данная точка находится от образующего вектора. Для оставшихся точек можно сформулировать следующий алгоритм определения принадлежности к левой или правой части.
Положим некоторый планарный граф G равным графу топологической модели структурной модели.
Если в структурной модели существует ребро, которое пересекается с отрезком текущей разделяющей прямой между y1 и y2, то удалим из графа G соответствующее ему ребро.
Покрасим в черный цвет вершины графа G, соответствующие ключевым точкам или изгибам, которые находятся слева от образующего текущую разделяющую линию вектора и имеют значение y-координаты между значениями y1 и y2.
Аналогично, покрасим в белый цвет вершины графа G, соответствующие ключевым точкам или изгибам, которые находятся справа от образующего текущую разделяющую линию вектора и имеют значение y-координаты между значениями y1 и y2.
Для каждой вершины определим компоненту, к которой она относится.
Рассмотрим любую ранее не рассмотренную компоненту связности графа G.
Если в рассматриваемой компоненте связности имеются раскрашенные вершины только одного цвета, то покрасим все вершины этой компоненты связности в этот цвет и перейдем к шагу 9.
Если в рассматриваемой компоненте одновременно имеются вершины черного и белого цвета, то пометим текущую разделяющую линию как некорректную и завершим работу алгоритма.
Если в графе G имеются нерассмотренные компоненты связности, перейдем к шагу 6, в противном случае алгоритм закончен.
Описанные критерии позволяют выделить на исходной структурной модели все возможные разделяющие линии, которые, в свою очередь, образуют множество линий-кандидатов L. Задача сегментации отдельного слова рукописного текста была сведена к задаче сегментации структурной модели, которая впоследствии была сведена к задаче выбора подмножества прямых из множества линий-кандидатов L, которыми будет выполнено разделение структурной модели слова на отдельные участки.
Для каждой прямой известны: ее уравнение, начало и конец вектора, которым образована эта прямая, а также подмножества ключевых точек и изгибов, по каждую из сторон этой разделяющей прямой.
Обозначим как G(S) – значение степени схожести участка топологической модели, содержащего все точки интереса из множества S и соединяющие ребра, оба конца которых находятся в этом множестве.
Введем функцию F(S) – максимальное суммарное значение степеней схожести при разделении множества точек интереса S некоторым подмножеством разделяющих линий из множества L.
Для того чтобы определить значение функции F(S) для некоторого множества точек интереса S, необходимо рассмотреть все разделяющие прямые множества L, которые разбивают множество S на два непустых подмножества. Пусть прямая li разбивает множество S на непустые подмножества S1(i) и S2(i). Тогда, рассматривая все допустимые прямые li, можно вычислить значение F(S), используя рекуррентную формулу
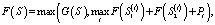 (*)
(*)
где Pi – величина штрафа за неиспользование участка структурной модели в процессе классификации.
Суть выражения (*) заключается в выборе варианта разбиения множества S таким образом, чтобы максимизировать суммарную величину степени схожести. Рассматриваются все варианты разбиения разделяющими прямыми множества L и вариант, при котором все точки множества S относятся к одному символу, и, следовательно, дальнейшее разбиение не производится.
Вычисление функции F(S) ввиду рекуррентности ее аналитического представления имеет экспоненциальную вычислительную сложность. Однако использование кеширования уже посчитанных значений функции F(S) для определенных множеств S существенно улучшает быстродействие алгоритма вычисления этой функции. Высокое быстродействие вычислений с использованием кеширования объясняется малым количеством возможных множеств S, для которых необходимо вычислить значение функции F(S). В свою очередь, малое количество возможных множеств можно объяснить спецификой способа их получения. Каждый раз, за редкими исключениями, множество точек интереса фактически разбивается на две подмножества: по левую и по правую сторону от разделяющей линии. Таким образом, количество различных множеств на практике имеет квадратичную зависимость от количества точек интереса.
Подход к вычислению функции F(S) можно охарактеризовать как применение метода динамического программирования [1]. При таком подходе состояние будет кодироваться некоторой хэш-функцией от множества S, а количество состояний, на практике квадратично зависит от элементов исходного множества, для которого необходимо вычислить значение функции.
В качестве хэш-функции можно использовать легко вычислимый полиномиальный хэш, который позволит представить каждое из множеств в виде соответствующего 64-битного целого числа. Хэширование множества можно выполнить, хэшируя упорядоченный массив номеров точек интереса, которые входят в данное множество.
Результаты тестирования и выводы
Для исследования быстродействия алгоритма сегментации рукописных слов на основе построения структурной модели с применением динамического программирования были выполнены начертания слов различной длины, составляющих панграммы. Для оценки степени схожести отдельных символов тем же почерком были выполнены начертания отдельных рукописных символов. Отдельные символы были начертаны так, чтобы их графические представления были максимально похожи на те, что встречаются в составе рукописных слов.
Примеры начертаний отдельных слов, которые были использованы для исследования быстродействия алгоритма сегментации, приведены на рис. 4.
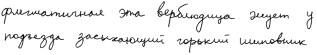
Рис. 4. Графические начертания рукописных слов
Каждое слово приведенной панграммы было записано 20 раз одним и тем же почерком. Начертания одних и тех же слов при исполнении имеют существенные отличия, поэтому для оценки быстродействия были использованы все полученные начертания слов.
В ходе тестирования алгоритма сегментации выполнялся его запуск для каждого из изображений начертаний. В процессе работы алгоритма определялись следующие параметры: время работы алгоритма, количество линий-кандидатов и количество состояний в методе динамического программирования.
Результаты тестирования, приведенные в таблице, демонстрируют, что средние количества точек интереса, линий-кандидатов и состояний динамического программирования являются величинами, несущественно влияющими на потребление оперативной памяти. Более того, количество состояний динамического программирования, одновременное являющееся и количеством элементов в хэш-таблице, на практике оказывается настолько небольшим, что общее время работы ни на одном из изображений не превысило 1,7 с для процессора Intel Core i5-4200 (1.60GHz, 2.30GHz) без использования графических ускорителей.
Результаты тестирования быстродействия
|
Слово |
Ср. кол-во точек интереса |
Ср. кол-во линий-кандидатов |
Ср. кол-во состояний |
Ср. время работы, с |
|
Флегматичная |
77,10 |
156,50 |
12275,90 |
1,448 |
|
Эта |
27,45 |
57,70 |
1739,55 |
0,392 |
|
Верблюдица |
71,95 |
146,05 |
10692,95 |
1,292 |
|
Жует |
46,40 |
95,70 |
4636,60 |
0,693 |
|
У |
10,00 |
20,75 |
252,55 |
0,230 |
|
Подъезда |
58,95 |
119,80 |
7204,20 |
0,946 |
|
Засыхающий |
82,80 |
168,40 |
14208,90 |
1,669 |
|
Горький |
43,25 |
87,00 |
3855,80 |
0,599 |
|
Шиповник |
59,950 |
122,450 |
7531,050 |
0,978 |
Отдельно можно исследовать сделанное ранее предположение о зависимости количества состояний динамического программирования от количества линий-кандидатов. Предполагалось, что такого рода зависимость будет близка к квадратичной. Для подтверждения данной гипотезы была построена квадратичная аппроксимирующая исследуемой зависимости. В качестве измеряемых данных были использованы пары значений для каждого изображения набора: количество линий-кандидатов и соответствующее ему количество состояний динамического программирования. Измеряемые данные, а также построенная для них квадратичная аппроксимирующая показаны на рис. 5.
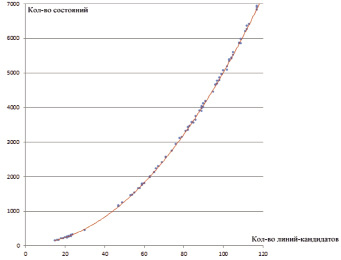
Рис. 5. Визуализация зависимости количества состояний динамического программирования от количества линий-кандидатов
Графическое представление результатов аппроксимации наглядно демонстрирует, что зависимость количества состояний динамического программирования от количества линий-кандидатов, как и предполагалось, близка к квадратичной. Отклонения от квадратичной зависимости в меньшую сторону объясняются недостижимостью некоторых состояний из-за пересечений определенных линий-кандидатов.
Следует также отметить, что величина отклонений значений, полученных опытным путем, увеличивается с ростом количества линий-кандидатов.



