Многие прикладные задачи распределенных систем сбора, хранения и передачи видеоинформации включают в себя не только процессы повышения ее качества, сжатия, преобразования форматов, но и сохранения ее конфиденциальности. Это характерно для систем мониторинга территорий, многофункциональных систем регистрации (МСР™), распределенных промышленных систем, видеосистем охраны и др., использующих открытые сети для построения их инфраструктуры [7].
В таких системах перед передачей исходное изображение полностью (или по фрагментам) преобразуется к шумоподобному виду – маскируется [6]. Преобразованное изображение передается по открытым сетям (в том числе и беспроводным), где оно оказывается под угрозой негласного несанкционированного использования. При получении преобразованного изображения на приемной стороне выполняется обратное преобразование, в результате которого происходит восстановление исходного изображения.
Одним из эффективных методов сохранения конфиденциальности является использование матричных операций в преобразовании изображений. Использование матричной арифметики характерно для обработки изображений как массива пикселей. Для преобразования могут быть использованы квадратные ортогональные по столбцам (строкам) матрицы Адамара [14], жакетные матрицы [13], матрицы Белевича [12]. В работах [1, 2, 4, 5, 8–10, 15] состав матриц и методы преобразования изображений значительно расширены новыми предложениями.
Во-первых, матрицы Адамара и Белевича, определенные исключительно на четных порядках вида 4t и 4t + 2, где t – натуральное число, в основном уже известны либо легко подбираются. Во-вторых, современные видеосистемы оперируют с изображениями 4К, 8К и более, для которых нужны маскирующие ортогональные матрицы больших размеров с небольшим количеством значений элементов. В-третьих, нестандартные размеры изображений при использовании функции Quality Box требуют наличия квадратных матриц, в том числе нечетных порядков.
В настоящей работе рассматриваются варианты двустороннего матричного маскирования изображений с использованием квадратных квазиортогональных матриц Мерсенна, расширяющих класс матриц Адамара для нечетных порядков 4t – 1 и имеющих так же, как и они, два значения элементов. Исследуется вопрос существования изображений, инвариантных к рассматриваемым преобразованиям – изображений, не изменяемых маскированием.
Двустороннее матричное маскирование
Схема маскирования/демаскирования передаваемых изображений в канале, в котором возможен несанкционированный доступ, показана на рис. 1. Здесь М – квадратная ортогональная матрица порядка n, Р – исходное и восстановленное изображения.
Рис. 1. Маскирование/демаскирование при передаче изображений
Первый этап преобразования состоит в разбиении исходного изображения Р на N одинаковых по размеру квадратных фрагментов размера n×n, обозначенных как X. Неполные фрагменты дополняются нулями до полных. Оператор, осуществляющий указанную фрагментацию изображения, обозначен на рис. 1 символом S.
На втором этапе исходное изображение P, разбитое на фрагменты, рассматривается как блочная матрица, состоящая из квадратных матриц вида Х. Для преобразования изображения столбцы, а затем строки ее фрагментов X умножаются на столбцы матрицы M (двустороннее матричное преобразование) согласно формуле
Y = M T X M. (1)
Cформированное из фрагментов Y изображение поступает в коммуникационный канал, передается и на приемном конце подвергается обратному двустороннему преобразованию для получения фрагментов исходной матрицы по формуле
X = (M T)–1Y M –1. (2)
Результирующее изображение P является итогом применения обратного оператора S–1, осуществляющего дефрагментацию из фрагментов вида X принятого изображения. В работах [5, 6] предлагается использовать ортогональные матрицы M (M –1 = M Т), так как это упрощает вычисления (2) до формулы X = M Y M T, приведенной на рис. 1. В этом случае обратное преобразование совпадает с прямым с точностью до транспонирования маскирующей матрицы, а также отпадает необходимость отдельно хранить или вычислять обратную матрицу, что экономит память при непосредственной реализации метода в системе.
В качестве примера на рис. 2 приведены оригинальное изображение и результат его маскирования, полученный с использованием описанного выше способа.
Рис. 2. Оригинальное и маскированное изображения
Выбор ортогональных матриц маскирования
При разбиении исходного изображения на фрагменты с целью получения блочной матрицы изображения, выбирается размер блока изображения. Выбор делается исходя из размеров используемой для маскирования матрицы. Здесь решается задача определения матрицы M, которая обеспечит лучшее приближение результата двустороннего умножения изображения к шумоподобному виду и обеспечит меньшее время преобразования всего исходного изображения.
Поскольку основная преследуемая маскированием цель – максимально уравнять значения элементов преобразованной матрицы, то решается задача поиска в классе ортогональных матриц заданного размера таких матриц M, у которых максимальный по модулю элемент минимален. Хорошо известное решение этой задачи относится к случаям, когда размер матриц кратен четырем – это нормированные матрицы Адамара. Решение для четных размеров, не кратных четырем, дают так называемые конференц-матрицы, имеющие нулевую диагональ и остальные элементы равные ± 1 [1, 12].
Для нечетных порядков матриц общее решение задачи поиска ортогональных матриц с минимальным по модулю максимальным элементом получить несложно, но такие матрицы будут иметь большое число значений элементов (уровней). Число уровней оптимальных в указанном смысле ортогональных матриц линейно растет для n = 3, 5, 7, 9, 11, причем при n = 13 происходит структурное перестроение с резким ростом как претендентных на оптимум матриц, так и числа уровней. Соответственно, использование таких матриц проблематично.
В работе [3] предлагается заменить строго оптимальные матрицы локально оптимальными матрицами Мерсенна порядков n = 2k×1 и аналогичными для n = 4t – 1, которыми можно заменить строго оптимальные матрицы.
Матрицы Мерсенна
Приведем некоторые определения.
Определение 1. Ортогональной матрицей называется квадратная матрица A порядка n такая, что ATA = I, где I – единичная матрица.
Определение 2. Квазиортогональной матрицей называется квадратная матрица A порядка n с ограниченными по модулю элементами |aij| ≤ 1, такая, что ATA = ω(n)I, где I – единичная матрица, ω(n) – весовая функция.
Локальный максимум детерминанта квазиортогональной матрицы достигается, если любое достаточно малое по параметрам изменение матрицы не нарушает вида уравнения связи ATA = ω(n)I при свободно заданном значении веса ω(n), но приводит к уменьшению детерминанта.
Допустимыми являются любые изменения параметров варьируемой матрицы, не нарушающие условие ортогональности ее столбцов. Весовая функция в задачах поиска условного максимума |det(A)| при ограничении вида ATA = ω(n)I заранее не задана и сама является предметом поиска. В этом состоит важное их отличие от задачи поиска матриц Адамара с жестко заданным заранее весом ω(n) = n.
Квазиортогональные матрицы порядков n = 2k, вложенных в последовательность 4t, выделены еще Сильвестром ввиду их орнаментальных свойств – способности создавать сложный фрактальный узор при исключительно простом правиле инверсии (транспонированием с масштабированием). Аналогично можно построить квазиортогональные матрицы порядков n = 2k - 1, вложенных в последовательность 4t - 1, и обладающих локальным максимумом детерминанта. Последовательность 2k - 1 называется последовательностью чисел Мерсенна.
Определение 3. Матрица Мерсенна [3, 11] – это квазиортогональная матрица M порядка n с элементами a = 1 и –b, где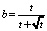 
для n = 2k-1.
Классический способ построения матриц Адамара Hn порядков n = 2k основан на использовании итерационной формулы Сильвестра
,
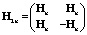где в качестве начального значения используется число H1 = 1. Модифицированная формула Сильвестра [16] для вычисления матриц Мерсенна выглядит как
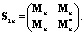
Здесь матрица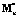 
образована не сменой знака, а перестановкой элементов a и –b. Полученная по этой формуле матрица S2n симметрична, но ее порядок четен и на единицу меньше порядка следующей матрицы Мерсенна M2n+1. Для рекурсивного перехода от матрицы к матрице одного лишь удвоения порядка недостаточно, необходимо дополнительное окаймление матрицы S2n добавлением строки и столбца 
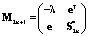. Здесь λ, e – соответственно собственное число и собственный вектор матрицы S2n. Полученная таким образом матрица будет симметричной и квазиортогональной. Справедливость положения следует непосредственно из условия ортогональности столбцов матрицы.
В окончательной версии алгоритма не требуется решать проблему собственных значений, поскольку если выбрать в качестве начальной симметричную матрицу
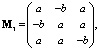
то собственное значение матрицы удвоенного порядка будет λ = –a. При этом половина компонент собственного вектора состоит из –b, остальная половина – из a.
Особые изображения двустороннего матричного маскирования
Пусть исходное изображение разбито на N одинаковых матриц Х размером n×n. Поставим задачу найти изображения, которые инвариантны к преобразованию (1), т.е. переводятся им в то же изображение с точностью до постоянного множителя – M T X M = λ X. Такие изображения называют собственными, корневыми или особыми изображениями преобразования. Число λ – соответствующим особым или корневым числом. Если исходное изображение совпадет с особым изображением используемого преобразования, то маскированное изображение совпадет с исходным и эффект маскирования достигнут не будет.
Ортогональные матрицы M с собственными значениями |λ| = 1 не усиливают изображения. При умножении на M слева поиск особых изображений сводится к стандартной задаче определения перестановочных друг с другом матриц X M = M X (или X M = – M X).
Из матричной алгебры известно, что матрицы перестановочны (коммутируемы), если они построены на одинаковом наборе собственных векторов. Для симметричных матриц M собственные числа вещественны, а собственные векторы – ортогональны. В частности, коммутируема сама с собой матрица X = M, поскольку она, безусловно, построена на том же наборе собственных векторов, что и преобразующая матрица, и M T X = I – единичная матрица. Иными словами, наиболее беззащитны изображения, похожие на преобразующую матрицу, и для успешного маскирования ей самой выгодно выглядеть хаотичной. Это качество разделяют между собой все матрицы расширяемого семейства Адамара, включая матрицы Мерсенна.
Пример
Для маскирования фрагментов изображения P будем использовать матрицы Мерсенна. На рис. 3 для примера приведены визуализованные в «портретах» матрицы Мерсенна порядков 7, 15, 31 и 255, на которых квадраты белого и черного цветов соответствуют значениям а и –b элементов этих матриц.
Рис. 3. «Портреты» матриц Мерсенна порядков 7, 15, 31 и 255
Строки и столбцы матриц Мерсенна, как и матриц Адамара, ортогональны. Для применения в алгоритмах преобразования их нормируют так, чтобы фробениусовы нормы строк и столбцов были единичны. Каноническое разложение нормированной матрицы Мерсенна на матрицу собственных векторов V и диагональную матрицу собственных значений имеет вид M = VDV–1. Собственные значения ортогональных матриц равны 1 или – 1.
Умножение на матрицу M можно рассматривать как умножение на ортогональную матрицу V–1 (поворот изображения), собственно кодирование при помощи знакопеременной матрицы D = diag(1, – 1, …, 1) и обратный поворот V. Особое изображение индифферентно к этому процессу, если состоит (частично) из инверсных операций: обратного поворота, любой диагональной матрицы D* и поворота. При двустороннем преобразовании матрица DD*D = D*, т.е. не меняется. Отсюда следует алгоритм построения особых изображений, состоящий в вариации матрицы собственных чисел ортогональной матрицы M и ее реконструкции P* = VD*V–1.
На рис. 4 приведены по два «портрета» вычисленных корневых изображений P* для приведенных на рис. 3 матриц. Квадраты различного оттенка серого соответствуют визуализированным пикселям реального изображения.
Рис. 4. «Портреты» особых изображений для матриц Мерсенна порядков 7, 15, 31, 255
Представленные изображения инвариантны по отношению к рассматриваемому преобразованию с использованием матриц Мерсенна. Они являются «портретами» объектов, которые не имеют отношения к множеству объектов реального мира – объектов, изображения которых передаются в рассматриваемых видеосистемах. Следовательно, можно смело утверждать, что матричное двустороннее маскирование матрицами Мерсенна может быть использовано в системах без каких-либо ограничений, вносимых изображениями, инвариантными к преобразованию (1).
Заключение
Расширение класса ортогональных матриц четных порядков, используемых для маскирования изображений, матрицами Мерсенна нечетных порядков позволяет расширить возможности при реализации систем.
Для двустороннего матричного маскирования изображений матрицами Мерсенна, как и другими матрицами, существуют особые изображения, инвариантные по отношению к указанному преобразованию. Рассмотренный способ поиска особых изображений, проиллюстрированный конкретными примерами для матриц Мерсенна разных порядков, позволяет утверждать, что он может быть использован без ограничений. Особые изображения не являются портретами объектов реального мира.
Рассмотренные преобразования и примеры полученных особых изображений относятся только к монохромным изображениям, поскольку только они представляются в виде матрицы, которая состоит из числовых значений отдельных пикселей. Именно эта матрица и подвергается фрагментации при матричном преобразовании, если маскирующая матрица значительно меньше изображения.
Для цветных изображений маскирование применимо, но алгоритм реализации усложняется. Например, при представлении цветных изображений трехслойной матрицей RGB, маскированию будет подвергаться отдельно каждый из трех слоев матрицы изображения.
Работа выполнена при поддержке Минобрнауки РФ при проведении научно-исследовательской работы в рамках проектной части государственного задания в сфере научной деятельности по заданию № 2.2200.2017/ПЧ.