Прямые спектральные задачи по колебаниям механических систем рассмотрены во многих трудах по теории колебаний, в том числе И.И. Артоболевского, И.М. Бабакова, И.И. Блехмана, В.В. Болотина, С.П. Стрелкова, С.П. Тимошенко [3, 11]. Изучение обратных спектральных задач ведет свое начало с фундаментальных работ В.А. Амбурцумяна и Г. Борга. Значительный вклад в становление этого направления внесен трудами А.Н. Тихонова, Б.М. Левитана, В.А. Марченко, М.Г. Гасымова, В.А. Юрко, Г.М.Л. Гладвелла и других [12, 13].
Задачам акустической диагностики механических систем, составляющими которых являются и оболочки, посвящено также множество работ, в том числе работы [1, 2, 4, 5, 7, 13]. Ранее в работах автора [2, 8–10] изучалось диагностирование закреплений валов, полых труб и труб с жидкостью по собственным частотам их колебаний. В данной же работе ставится обратная задача определения физических параметров тонкостенной круговой цилиндрической оболочки по известным собственным частотам ее свободных колебаний. Доказывается единственность решения задачи, приводится метод решения задачи.
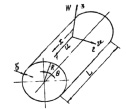
Круговая цилиндрическая оболочка
Прямая задача определения частот колебаний оболочки
Известные стандартные допущения [2] для таких оболочек позволяют решать задачу колебаний в линейной постановке с малой погрешностью порядка δ/R в сравнении с единицей. Здесь δ – толщина оболочки, а R – радиус её срединной поверхности (рисунок).
Положение произвольной точки срединной поверхности оболочки определяется цилиндрическими координатами (x, θ), где x – расстояние от начального сечения до точки по образующей, θ – угловая координата, отсчитываемая от начального радиуса.
Области изменения значений координат ограничены пределами 0 ≤ x ≤ L, 0 ≤ θ ≤ 2π, где L – длина оболочки. Перемещения произвольной точки срединной поверхности рассматриваются в декартовой системе координат, связанной с недеформированной срединной поверхностью таким образом, что ось 1 направлена по образующей, ось 2 – по касательной к направляющему кругу, а ось 3 – по радиусу оболочки. Обозначим компоненты перемещений по этим осям соответственно u, ν и w.
Система дифференциальных уравнений, описывающая свободные колебания оболочки, известна и имеет вид [2]
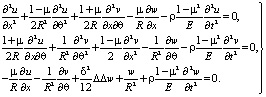(1)
Здесь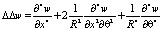 
– оператор Лапласа, μ – коэффициент Гука, E – модуль Юнга, ρ – плотность материала оболочки.
Любая задача динамики круговой цилиндрической оболочки сводится к необходимости решения этой системы с соответствующими краевыми условиями. Пусть эти условия отражают свободное опирание краёв оболочки, т.е. при x = 0, L имеем
; 
; 
; 
;
; 
; 
; 
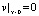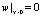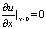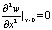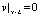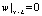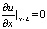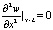. (2)
Решение системы уравнений (1) для каждого из перемещений при собственных колебаниях оболочки рассмотрим в виде одного члена такого ряда:
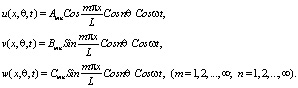
Здесь ω – частота, Amn, Bmn, Cmn – амплитуды собственных колебаний оболочки.
Подставим решения в систему уравнений (2) и после преобразований получим однородную систему относительно амплитудных значений Amn, Bmn, Cmn:
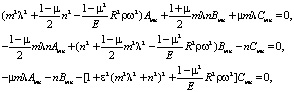
в которой
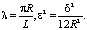(3)
Учитывая условие существования ненулевых решений последней системы уравнений, а именно равенство нулю определителя системы, получим частотное уравнение:
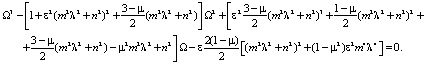(4)
ЗдесьΩ – безразмерный частотный параметр, определяемый как
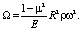(5)
Корни Ω частотного уравнения соответствуют значениям квадратов частот колебаний ω2, при которых оболочка имеет отличные от нуля амплитудные значения.
Для каждого сочетания чисел m, n уравнение (4) имеет три вещественных положительных корня, которые соответствуют квадратам частот трёх основных видов колебаний. Поскольку числа m и n могут принимать любые целые значения от единицы до бесконечности, то для каждого из трёх видов колебаний существует бесконечное число собственных частот и форм колебаний.
Решение прямой задачи рассмотрим на примере.
Пример 1. Определить частоты колебаний тонкостенной цилиндрической оболочки, для которой известны следующие физические параметры:
R = 0,05 м, L = 1 м, δ = 0,007 м, m = 2, n = 2,
μ = 0,28, E = 210•109 Па,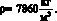 
Решение. Подставляя заданные физические параметры оболочки в частотное уравнение (4), получим
– Ω3 + 6,6015 ?2 – 8,0898 Ω + 0,3597 = 0.
Решение последнего уравнения, найденное с помощью ЭВМ, имеет вид
Ω1 = 0,0462; Ω2 = 1,5583; Ω3 = 4,9969.
Найдем соответствующие безразмерным корням собственные частоты колебаний оболочки, используя соотношение (4):
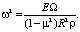(6)
В соответствии с (6) имеем: Ω1 = 0,7319 ГГц; Ω2 = 4,2509 ГГц; Ω3 = 7,6122 ГГц.
По решению прямой задачи исследовано влияние на собственные частоты колебаний тонкостенной цилиндрической оболочки таких параметров, как радиус, длина и толщина оболочки [10].
Обратная задача диагностирования характеристик оболочки и метод ее решения
Поставим к прямой спектральной задаче обратную – задачу диагностирования характеристик оболочки по известным частотам ее собственных колебаний.
Итак, обратная задача: Известны собственные частоты колебаний оболочки. Неизвестны характеристики оболочки, а значит, неизвестны коэффициенты λ и ε2 уравнения (4), содержащие в себе искомые физические параметры.
Исследуем вопрос о единственности решения поставленной задачи определения коэффициентов λ и ε2. Преобразуем частотное уравнение (4) к следующему виду:
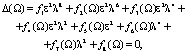(7)
в котором fi(Ω) (i = 2,..,8) выражаются через физические параметры оболочки. Задачу с частотным уравнением (7) обозначим через L, а задачу с таким же частотным уравнением, но с другими коэффициентами λ' и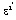 
, обозначим через L'.
Теорема (о единственности решения). Если собственные частоты задач L и L' с характеристическими определителями Δ(Ω) и Δ'(Ω) совпадают с учетом их кратностей, то λ = ε2 и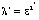 
.
Доказательство. Собственные частоты задачи L совпадают с корнями уравнения (7) (или уравнения (4)). Уравнение (7) является целой функцией от Ω = Ω(ω). Функции fi(Ω) (i = 2,..,8) не зависят от коэффициентов λ и ε2, и образуют систему линейно независимых функций. Для частотного уравнения задачи L' имеем аналогичное уравнению (7) представление:
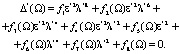
Поскольку Δ(Ω) и Δ’(Ω) являются целыми функциями от Ω = Ω(ω) и не равны тождественно нулю, то из теоремы Адамара [6] получаем, что они восстанавливаются по своим нулям с точностью до постоянного множителя K. Значит, Δ(Ω) – KΔ'(Ω) ≡ 0. Из последнего равенства и линейной независимости функций fi(Ω) (i = 2,..,8) получаем, что K = 1, отсюда λ = ε2 и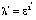 
. Теорема доказана.
Построим теперь метод решения обратной задачи, а именно, метод нахождения коэффициентов λ и ε2 по известным трем собственным частотам колебаний цилиндрической оболочки. Пусть даны собственные частоты ω1, ω2 и ω3 колебаний оболочки, а значит, известны значения трех безразмерных частот колебаний Ω1, Ω2, Ω3.
Подставив значения безразмерных частотΩ1, Ω2 в (7), получим систему
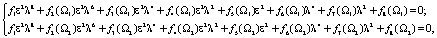(8)
имеющую несколько пар решений относительно (λ, ε). Аналогичным образом решим систему
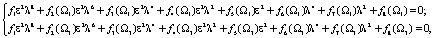(9)
подставив в (7) значения безразмерных частот Ω1 и Ω3. Система уравнений (9) также будет иметь несколько решений относительно неизвестных коэффициентов. Общим решением систем уравнений (8) и (9) является лишь один набор значений λ, ε),который и является искомым. Применение данного метода рассмотрим на примере.
Пример 2. Определить длину и толщину тонкостенной круговой цилиндрической оболочки, для которой известны частоты собственных колебаний ω1 = 0,7319 ГГц, ω2 = 4,2509 ГГц, ω3 = 7,6122 ГГц, а также параметры оболочки: R = 0,05 м, μ = 0,28, E = 210•109 Па,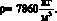 
Решение. Заданные собственные частоты i и известные физические параметры оболочки подставим в равенства (5) и найдем соответствующие значения безразмерных частот: Ω1 = 0,0462; ω2 = 1,5583; ω3 = 4,9969. Подставляя значения Ω1 и Ω2 в систему уравнений (8), получим
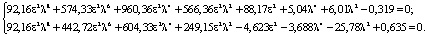
Решая полученную систему с помощью программы, получим 23 пары решений относительно коэффициентов λ и ε2, из которых только следующие пары решений имеют физический смысл: (ε2 = 0,4116; λ = 0,4517); (ε2 = 0,0404; λ = 0,157).
Подставляя теперь значения безразмерных частот Ω1 и Ω3 в систему уравнений (9), имеем
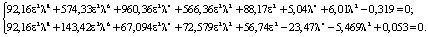
Решением последней системы уравнений относительно коэффициентов λ и ε2 получим также 23 пары решений, из которых физический смысл имеют следующие пары решений: (ε2 = 0,0404; λ = 0,157); (ε2 = 0,1895; λ = 0,8326). Общим решением обеих систем уравнений является один набор: (ε2 = 0,0404; λ = 0,157).
Используя теперь формулы
, 
,
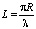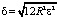найдем толщину и длину оболочки:
,
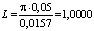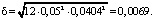
Таким образом, длина и толщина оболочки, соответствующие заданным значениям частот колебаний оболочки, равны L = 1 м, δ = 0,007 м.
Заключение
В работе исследована прямая задача определения собственных частот колебаний тонкостенных круговых цилиндрических оболочек. Показано, что математическое моделирование рассмотренного колебательного процесса приводит к определению трех безразмерных частот колебаний оболочки и соответствующих трех размерных собственных частот ее колебаний.
Приведены постановка и решение обратной задачи – задачи определения характеристик цилиндрической оболочки по известным частотам ее собственных колебаний. Исследована и доказана единственность решения обратной задачи. Приведен метод решения при известных значениях трех частот колебаний оболочки, который сведен к решению двух систем нелинейных уравнений относительно двух неизвестных параметров. Приведены конкретные примеры, подтверждающие выводы.
Методы решений обратных задач можно использовать при решении проблемы сохранения безопасных частот колебаний оболочки при изменениях ее физических характеристик.