При проектировании систем управления многими динамическими объектами в условиях параметрической неопределенности, как правило, известны только оценки параметров объекта управления в виде верхних и нижних граничных значений, либо задана принадлежность параметров некоторому множеству. К таким объектам относятся биотехнологические объекты стадии ферментации фармацевтических и микробиологических производств [4]. Поэтому проектируемые регуляторы должны обеспечивать устойчивость и качество не одной системы управления, а целого семейства систем, соответствующих различным значениям параметров объекта. Это достигается путем придания системам свойств робастной устойчивости и робастного качества по отношению к параметрическим и иным возмущающим воздействиям за счет выбора структуры системы и синтеза соответствующих алгоритмов управления [1, 8].
Одним из методов синтеза таких алгоритмов управления является использование аппарата нечёткой логики [2, 7]. Однако общих рекомендаций по синтезу и анализу робастных систем для управления биотехнологическими объектами нет. В связи с этим актуальными являются вопросы анализа и синтеза робастной системы управления с нечетким регулятором на основе принципа переменной структуры, функционирующей в условиях параметрической неопределенности, нестационарности и при наличии запаздывания управляемых биотехнологических объектов. Под переменной структурой в данной работе понимается изменение связей между функциональными блоками нечеткой системы в зависимости от характера колебаний регулируемой переменной в переходном процессе системы.
Синтез нечеткого регулятора с переменной структурой
Повышение требований к качеству регулирования и увеличение числа факторов, оказывающих значимое влияние на функционирование объектов управления, ведут в общем случае к усложнению синтезируемых регуляторов. Практика же требует создания регуляторов как можно более простой структуры. К таким регуляторам из типовых можно отнести релейные, двух-, трехпозиционные регуляторы. Однако известно [4], что используемые к настоящему времени позиционные регуляторы не всегда обеспечивают заданное качество регулирования. В связи с этим для улучшения качества позиционного регулирования разработаны модифицированные варианты алгоритмов управления, полученные на основе аппроксимации характеристик нелинейных типовых элементов и различных их комбинаций непрерывными нелинейными функциями типа сигмоидных [4]. К последним относится регулятор, синтезированный на основе аппроксимации характеристик релейного элемента с зоной и без зоны нечувствительности с насыщением, названный аппроксимированным нелинейным функциональным регулятором – АНФ-регулятором [4]. Закон управления, реализуемый этим регулятором, имеет следующий вид:
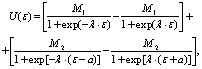(1)
где М1, М2 – величина регулирующего воздействия в зоне нечувствительности (ЗН) и за ее пределами соответственно; ε – ошибка регулирования; λ – коэффициент, определяющий наклон линейного участка характеристики регулятора; 2а – величина ЗН.
Структурно разрабатываемая интеллектуальная САУ содержит дополнительные блоки, которые выполняются как надстройка над АНФ-регулятором прямой цепи САУ, настраивая нужным образом его параметры (рис. 1). Основная функция, возлагаемая в данном случае на нечеткий регулятор (НР), – это формирование корректирующих поправок к коэффициентам настройки М1, М2 АНФ-регулятора в зависимости от текущего значения и скорости изменения ошибки регулирования. Функциональная схема нечеткой системы управления с использованием динамически корректируемого АНФ-регулятора приведена на рис. 1.
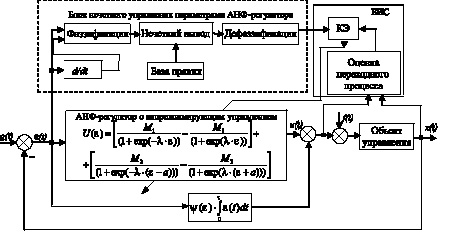
Рис. 1. Структурная схема нечеткой САУ с АНФ-регулятором в прямой цепи: КЭ – ключевой элемент; БИС – блок изменения структуры
Входными сигналами нечеткого регулятора выбраны сигнал рассогласования и его производная. Выходом – величина корректирующего воздействия на параметры М1, М2 АНФ-регулятора в прямой цепи системы. Для этого в лингвистических переменных нечеткой логики коррекция параметра М1, М2 представлена следующими пятью термами: сильно уменьшить (СМ), уменьшить (М), норма (Н), увеличить (В) и сильно увеличить (СВ).
Форма функций принадлежности для простоты математического описания выбрана треугольной. Числовые значения функций принадлежности выбраны исходя из возможных диапазонов изменения входных и выходной переменных, полученных при экспериментальном исследовании алгоритма аппроксимирующего управления [3, 4]. Известно, что степень пересечения во входных функциях принадлежности сильно влияет на статические характеристики нечеткого регулятора [5]. В то время как маленькие пересечения во входных функциях принадлежности формируют пороговые (ступенчатые) характеристики, большие пересечения делают кривую более гладкой. Пересечения в выходных функциях принадлежности меньше влияют на характеристику. Как видно из рис. 2, а, функции принадлежности для ошибки регулирования выбраны с небольшим пересечением оснований, так как гладкость кривой обеспечена параметрами аппроксимирующей функции.
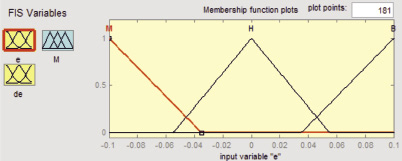
а)
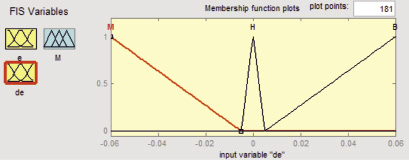
б)
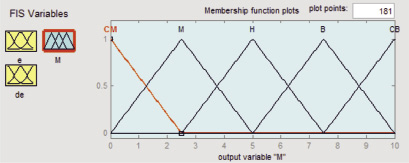
в)
Рис. 2. Графики функций принадлежности (а – ошибка, б – скорость изменения ошибки, в – корректируемый параметр регулятора)
Функция принадлежности входного сигнала ε(t) имеет два пересечения (перекрытия) на интервалах [– 0,055; – 0,035] и [0,055; 0,035], которые точно соответствуют диапазонам положительных наклонов кривой. Причиной тому является то, что два правила в этих диапазонах одновременно активны. С другой стороны, на диапазонах без пересечения только одно правило активно. Функция принадлежности выходного сигнала в этом случае зависит только от степени активности и, таким образом, центр тяжести функции принадлежности остается неизменным.
При синтезе системы использован алгоритм логического вывода по Мамдани как наиболее простой и позволяющий выносить суждение о том или ином параметре в виде утверждений, в отличие от их представления линейными функциями, характерного для нечеткого вывода Сугено. Значения функций принадлежности соответствующих нечётких переменных представлены в виде кусочно-линейных графиков, показанных на рис. 2.
Для дефаззификации переменных, т.е. для перехода от нечетких выводов к точному значению корректируемого параметра М, использован метод центра тяжести [9].
Следует заметить, что поскольку объект управления и АНФ-регулятор являются статическими звеньями, то при конечных значениях λ, М1, М2 в замкнутой САУ возникает статическая ошибка. Для сведения ее к нулю и придания системе свойства астатизма в алгоритм управления нечеткой системы с АНФ-регулятором введен интегратор с коэффициентом интегрирования ψ(ε). На основе вышеприведенных соображений и предложенного принципа управления в программном пакете Мatlab была реализована система с нечетким регулятором (рис. 1).
Результаты исследования нечёткой системы управления
В качестве объекта управления рассмотрен биореактор-ферментатор периодического действия по каналу регулирования температуры. При исследовании свойств системы удобно воспользоваться описанием объекта управления в виде передаточных функций [5]. Считаем априори известными значения параметров интервальной модели объекта, представленной в форме передаточной функции следующего вида:
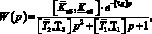(2)
в которой класс неопределенности задан неравенствами для коэффициента передачи объекта 
, для запаздывания 
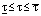, для постоянных времени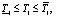 
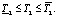Обозначения 
и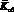 
соответствуют минимальному и максимальному значениям коэффициента передачи объекта. Аналогично и для других параметров модели.
Интервально-заданный объект управления с запаздыванием по каналу регулирования температуры в ферментаторе, аппроксимированный моделью c передаточной функцией вида
W(p) = Коб•ехр(– τ•p)/(T22•p2 + T1•p + 1), (3)
где 0,087 ≤ Коб ≤ 0,383; 14,35 ≤ T1 ≤ 41,56; 8,55 ≤ T2 ≤ 25,0; 2,2 ≤ τ ≤ 6,0, можно представить как семейство квазистационарных объектов.
Учитываем [6], что при описании объекта с параметрической неопределенностью номинальная модель располагается в центре множества. С учетом этого параметры номинальной модели объекта были заданы в виде среднеинтервальных значений:
=
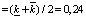[ °С / м3/ч];
=
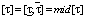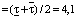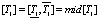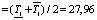мин;
=
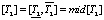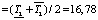мин;
=
мин.
где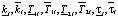 
– нижняя и верхняя граница коэффициента передачи объекта ki, постоянной времени Т1i, Т2i и запаздывания объекта τi соответственно; mid[νi] – середина интервального параметра [νi], i = 1,…,N.
Исследование нечёткой системы управления проведено путем имитационного моделирования при подаче на вход системы задающего воздействия θзад = 5 м.е. и подаче на вход объекта в различные моменты времени единичного ступенчатого воздействия f = 10 м.е. (м.е. – машинные единицы). В качестве значений параметров настройки АНФ-регулятора в основном контуре системы использованы следующие: М1 = М, М2 = М/2; λ = 0,2456; a = 0,1; M1 = 7, M2 = 14. Для анализа робастного качества проведены исследования САУ с моделью при неблагоприятном сочетании интервальных параметров объекта, которое характеризует предельно возможное качество робастного управления [1]. Полученные переходные процессы представлены на рис. 3.
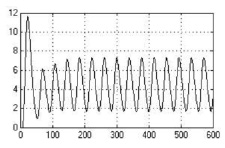
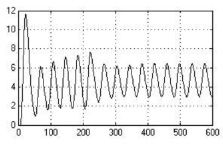
а) б)
Рис. 3. Переходные процессы в нечеткой САУ при выводе объекта на заданный режим (а) и действии возмущения на входе объекта в момент времени t = 200 мин (б) с моделью с неблагоприятным сочетанием параметров объекта: по оси ординат – регулируемая переменная, по оси абсцисс – время в мин
Из рис. 3 видно, что настройка нечеткого АНФ-регулятора, выполненная с использованием номинальной модели объекта, не исключает автоколебания при выводе на режим объекта при наихудшем сочетании параметров и поэтому не является оптимальной. Известно, что значительный ряд технологических процессов, особенно процессов биосинтеза, реакторных, химических и др., не допускает автоколебательного режима. Следовательно, существует необходимость в автоматической подстройке параметров регулятора или коррекции структуры системы. Однако подстройка параметров λ и М алгоритма управления (1) не приводит к положительному результату. Так, с уменьшением М уменьшается колебательность, но затягивается переходный процесс и имеет место статическая ошибка (при отсутствии интегрирующего звена). В связи с этим в данной статье рассмотрено решение задачи с помощью изменения структуры системы.
Для изменения структуры САУ (рис. 1) в состав нечеткого регулятора введена дополнительная корректирующая логическая связь по динамике переходного процесса. Возможны различные оценки динамики переходного процесса. Например, если ошибка большая (положительная или отрицательная) и скорость ее изменения большая, но другого знака, то сигнал управляющего воздействия НР должно быть минимальным, так как ошибка быстро уменьшается. Эта ситуация характерна для колебательного, но затухающего переходного процесса и учитывается базой правил. В случае критической ситуации, т.е. при возникновении автоколебаний, когда знак сигнала управляющего (корректирующего) воздействия НР совпадает со знаком скорости выходной переменной объекта, сигнал управляющего (корректирующего) воздействия НР должен обнуляться и оставаться ненулевым при противоположных знаках. Для критической ситуации оценку динамики переходного процесса можно получить, используя информацию об амплитуде отклонения регулируемой переменной от заданного значения (положительно большое или отрицательно большое).
В установившемся режиме и при других параметрах модели объекта из интервала неопределенности система работает с прежней базой правил, обеспечивая оптимальное соотношение между временем регулирования, максимальной динамической ошибкой и количеством колебаний. Это подтверждается полученными переходными процессами при различных параметрах интервального объекта (рис. 4) и при подаче на вход регулятора и объекта ступенчатых воздействий. Переходные процессы были исследованы для трех режимов:
режим 1 – переходный процесс при выводе объекта на установившийся режим при воздействии ступенчатого сигнала по заданию θзад = 5 м.е. в момент времени t = 0;
режим 2 – переходный процесс при выводе объекта на установившийся режим при воздействии ступенчатого сигнала по заданию θзад = 5 м.е. в момент времени t = 0 с и ступенчатого возмущения на входе объекта f = 10 м.е., действующего в момент времени t = 200 мин, демпфированного звеном c передаточной функцией W(p) = 0,2/(20p + 1) (поскольку мгновенные скачки в технологии отсутствуют);
режим 3 – переходный процесс при выводе объекта на установившийся режим при воздействии ступенчатого сигнала по заданию θзад = 5 м.е. и скачкообразного возмущения на входе объекта f = 10 м.е. в момент времени t = 0.
Графики переходных процессов представлены на рис. 4.
Из полученных процессов регулирования видно, что нечеткая система с переменной структурой исключает недопустимые автоколебания в системе (сохраняя при наихудшем значении запаздывания объекта τmax = 6 мин незначительные колебания регулируемой переменной в установившемся режиме).
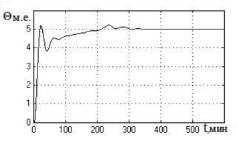
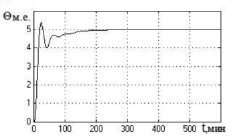
а) б)
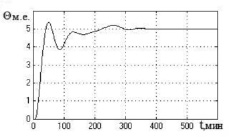
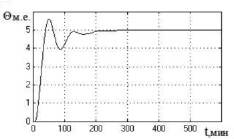
в) г)
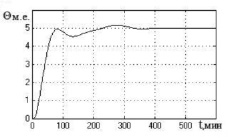
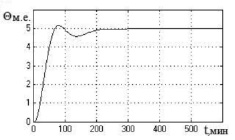
д) е)
Рис. 4. Графики переходных процессов в нечеткой САУ биореактором в режимах 1 и 2 (а, в, д) и режиме 3 (б, г, е) для модели объекта с параметрами: а, б – T1 = 18,36 мин; T22 = 104,74 мин2; K = 0,187; τ = 2,2 мин; в, г – T1 = 27,26 мин; T22 = 299,34 мин2; K = 0,128; τ = 6 мин; д, е – T1 = 41,56 мин; T22 = 625,72 мин2; K = 0,104; τ = 4 мин
Заключение
Разработанная структура САУ с минимальной базой правил нечеткого регулятора позволяет реализовывать робастную систему управления неопределенным и нестационарным биотехнологическим объектом с запаздыванием. При этом настройку НР целесообразно осуществлять с использованием номинальной математической модели объекта, параметры которой находятся усреднением их возможных значений в интервалах изменения. Анализ робастного качества управления целесообразно проводить с использованием модели объекта с наихудшим сочетанием параметров, значения которых принимаются из предельно возможных их изменений.
Выводы
К достоинствам разработанной нечеткой системы управления с переменной структурой, относящейся к категории интеллектуальных систем управления, можно отнести следующие возможности:
– реализовать любой требуемый для интервального объекта с запаздыванием нелинейный алгоритм управления, в том числе полученный на основе аппроксимации нелинейных характеристик с помощью сигмоидных функций;
- осуществлять настройку регулятора с аппроксимирующим управлением при неполном и неточном описании интервального объекта управления с запаздыванием при минимальной базе правил и количестве настроечных параметров;
– исключить предельные и резкие значения управлений при неопределенности параметров и возмущений и реализовать коррекцию, обеспечивающую робастность системы при нестабильности параметров объекта.
Построение системы управления на базе нечеткой логики является наиболее приемлемым вариантом построения САУ биотехнологическим объектом, а также другими объектами, аналогичными ему по динамическим и статическим свойствам.