Особенностью синтеза сложных технических систем (СТС) является выделение двух четко выраженных этапов – системно-агрегативного и структурно-параметрического синтеза.
Системно-агрегативный синтез помимо прочего предполагает обоснование показателей качества сложной технической системы и эффективности ее функционирования, а также критериев оценивания эффективности функционирования.
Структурно-параметрический синтез помимо прочего предполагает анализ эффективности функционирования СТС в условиях воздействия случайных и антагонистических факторов. Следовательно, при анализе и синтезе СТС, особую важность приобретает теория эффективности, без использования которой трудно получить оценку эффективности. Теория эффективности строится на понятии эффективности. Под эффективностью понимают комплексное операционное свойство целенаправленного процесса функционирования, характеризующее его приспособленность к выполнению стоящей перед системой задачи [4, 5].
Понятие эффективности напрямую связано с понятием качества. Качество – это свойство или совокупность свойств объекта, обусловливающих его пригодность для использования по назначению. Качество сложной системы проявляется в полной мере только в процессе ее функционирования, т.е. использования по назначению. Поэтому наиболее объективная оценка качества системы может быть получена по эффективности ее целевого применения [4, 5]. Эффективность невозможно «наблюдать» непосредственно, ее можно лишь определить косвенными методами.
Для определения эффективности вводится термин «критерий эффективности», под которым понимается условие, на основе которого определяется показатель эффективности [4, 5], выражающий меру соответствия достигнутых результатов требуемым значениям в отношении принятого критерия [1]. Критерии могут быть как векторными, если результаты функционирования СТС определяются совокупностью показателей, так и скалярными, если оценивание соответствия результатов функционирования заданным требованиям осуществляется на основе набора разнородных требований. Тогда удовлетворение требований по одному из показателей осуществляется на основе скалярного критерия.
Существуют две противоположные точки зрения на установление числа критериев в каждом конкретном случае [3].
Сторонники многокритериальных задач указывают на практическую невозможность соизмерения некоторых видов полезного эффекта и затрат, а следовательно, и невозможность использования единого обобщенного критерия эффективности.
С другой стороны, отмечается, что в случае применения для оценки эффективности и принятия решения нескольких критериев необходим какой-то алгоритм сопоставления показателей эффективности, в противном случае выбор решения невозможен. Необходим единый критерий эффективности для обеспечения выбора оптимального решения, к такому выводу приходят сторонники объединения критериев.
Для большинства СТС характерно наличие целого ряда критериев W1, W2,…, Wk и соответствующих им показателей П1, П2,…,Пk, одни из которых следует максимизировать, а другие – минимизировать.
Критерии эффективности можно разделить на три группы, характеризующие основные цели функционирования СТС.
1. Функциональные критерии эффективности, характеризующие степень приспособленности СТС к выполнению своих задач или степень соответствия результатов функционирования заданным целям.
2. Экономические критерии эффективности. На основе экономических критериев решаются следующие задачи: какой ценой достигается требуемый эффект функционирования СТС; какова стоимость создания СТС с заданными показателями функционирования; достижимы ли заданные показатели функционирования при имеющихся в наличии ресурсах.
3. Временные критерии эффективности функционирования. На основе временных критериев решаются, например, задачи по определению минимального времени подготовки СТС к применению или по оцениванию минимального времени выполнения поставленной задачи. Временному критерию чаще всего соответствуют показатели эффективности СТС в форме вероятности уложиться в определенные (заданные, гарантийные, директивные и т.п.) сроки.
При анализе и синтезе СТС решение о выборе системы в наибольшей степени соответствующей предъявленным требованиям по критериям эффективности требует решения многокритериальной задачи и не всегда может быть однозначным.
Выбору критериев эффективности, показателям эффективности и оценке обобщенной эффективности посвящено большое число работ в технической, экономической сферах и в других областях. Однако, несмотря на значительные успехи в развитии теории эффективности, есть вопросы, которые, на наш взгляд, требуют развития и уточнения.
Постановка задачи
Рассмотрим основные подходы к оценке эффективности функционирования СТС.
Стохастический подход к определению показателей эффективности предполагает использовать обобщенный показатель П, который определяется по выражению (1)
П = (Пн, Пп, Пэ), (1)
где Пн – комплексный показатель целевой надежности системы; Пп – комплексный показатель целевой производительности системы; Пэ – комплексный показатель целевой экономичности системы.
При этом комплексные показатели Пн, Пп, Пэ рассматриваются как числовые вероятностные характеристики
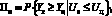 (2)
(2)
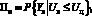 (3)
(3)
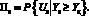 (4)
(4)
В выражениях 2, 3, 4 Uк ≤ Uц, Yк ≥ Yц, критерии эффективности W1, W2
Определять эти показатели эффективности предлагается по выражению
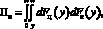 (5)
(5)
где Fк(y) – функция распределения возможного конечного результата функционирования и развития системы Yк; где Fц(y) – функция распределения целевого результата функционирования системы для достижения цели Yц;
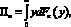 (6)
(6)
где y – переменная, выражающая возможные значения конечного результата функционирования и развития системы Yк;
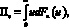 (7)
(7)
где u – переменная, выражающая возможные значения расхода ресурсов Uк на получение конечного результата Yк; Fк(u) – функция распределения случайной величины Uк.
На основании приведенных выражений необходимо получить аналитические выражения для функций Fк(y), Fц(y), Fк(u), представляющих собой функции распределения случайных величин Yк, Yц, Uк. Выбор вида функциональной зависимости является трудно формализуемым этапом и несет на себе отпечаток субъективности.
Детерминированные подходы к определению показателей эффективности предполагают оптимизировать некий обобщенный критерий эффективности. Задачи оптимизации обобщенного критерия эффективности в детерминированных подходах решаются по-разному.
Задача оптимизации обобщенного критерия эффективности по максимуму дроби.
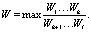 (8)
(8)
В числителе дроби критерии, которые следует увеличивать, а в знаменателе – критерии которые надо уменьшать. Недостатком подхода является компенсации низких значений критериев за счет уменьшения более высоких критериев. Отсюда вытекает неоднозначность выбора W1, Wk+1.
Задача оптимизации обобщенного критерия эффективности по максимуму разности критериев.
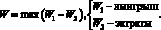 (9)
(9)
Недостаток подхода идентичен предыдущему.
Задача оптимизации обобщенного критерия эффективности по «взвешенной » сумме отдельных («частных») критериев эффективности и соответствующих им показателей
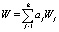 , (10)
, (10)
где aj – весовой коэффициент критерия эффективности Wj.
Недостатком подхода является субъективный подход к определению весовых коэффициентов aj критериев эффективности Wj.
Для сложных технических систем, процессы в которых протекают стохастически, дискретно, нестационарно, необходим подход к оценке эффективности, хорошо формализуемый с минимумом субъективности. Таким подходом может быть подход к оценке эффективности сложных технических систем с помощью обобщенных рядов Грама – Шарлье.
Решение задачи
Очертим класс сложных технических систем, для которых применим подход к оценке эффективности с помощью обобщенных рядов Грама – Шарлье. Это системы автоматические или автоматизированные (человеко-машинные, организационно-технические, эргатические, организационного управления) дискретные технологические системы (то есть такие сложные технические системы, в которых протекают дискретные технологические, процессы), функционирующие в условиях ограничений, наложенных на расходуемое количество ресурсов в сложных технических системах, с пополнением ресурсов или без пополнения.
Прежде чем перейти к оценке эффективности функционирования сложных технических систем, отметим, что в основе оценки эффективности функционирования лежит модель функционирования сложной технической системы, построенная в алгебре обобщенных рядов Грама – Шарлье.
Алгебраическая модель сложной технической системы является отображением в алгебре обобщенных рядов Грама – Шарлье графовой модели сложной технической системы. В основе графовой модели сложной технической системы лежит схема обработки. Для примера представим модель сложной технической системы в виде типового элемента схемы обработки (рисунок).
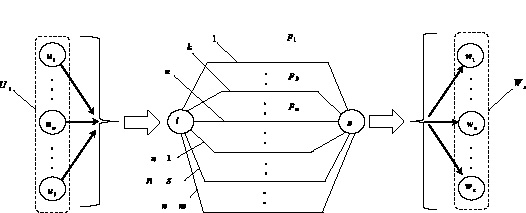
Представление сложной технической системы в виде типового элемента схемы обработки
Основой модели схемы обработки является типовой элемент, где Ui – множество номеров узлов схемы обработки, исходящих из которых дуги инцидентны i-му узлу; Wz – множество номеров узлов схемы обработки, инцидентные которым дуги исходят из z-го узла.
Запишем алгебраическую модель сложной технической системы, представленной в виде графовой модели на рисунке.
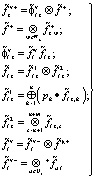 (11)
(11)
где 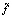 с индексами – частичная сумма обобщенных рядов Грама – Шарлье функции f плотности распределения вероятностей случайной величины
с индексами – частичная сумма обобщенных рядов Грама – Шарлье функции f плотности распределения вероятностей случайной величины 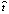 с соответствующими индексами.
с соответствующими индексами.
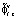 – частичная сумма обобщенных рядов Грама – Шарлье функции - плотности распределения вероятностей случайной величины
– частичная сумма обобщенных рядов Грама – Шарлье функции - плотности распределения вероятностей случайной величины 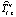 .
.
Трансформация типового элемента схемы обработки (за счет исключения тех или иных дуг) влечет однозначно соответствующую ей трансформацию модели (11) путем исключения частичных обобщенных рядов Грама – Шарлье. Как видно, модель позволяет автоматизировать процесс ее построения, это является важной особенностью метода моделирования в алгебре обобщенных рядов Грама – Шарлье.
При оценке эффективности, как отмечалось выше, наибольшие трудности возникают при определении функции распределения случайных величин (как правило затрат ресурсов и т.п.), так как приходиться строить условные законы распределения использованных ресурсов. Аналитически корректно это построение выполнить, как правило не удается, а численные эксперименты порождают дополнительные трудности и не всегда возможны.
Указанная проблема решается идентификацией СТС в терминах обобщенных рядов Грама – Шарлье. Другими словами, создается единый механизм одновременного, синхронного, функционально связанного формирования использованных ресурсов. Это позволяет оперировать с полученными на его основе законами распределения использованных ресурсов как с законами распределения условно независимых величин, то есть постулировать следующее равенство
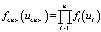 , (12)
, (12)
где 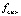 – плотность распределения вероятности случайного n-мерного вектора
– плотность распределения вероятности случайного n-мерного вектора 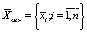 использованных ресурсов n видов;
использованных ресурсов n видов;
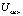 n-мерный вектор
n-мерный вектор 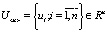 ;
;
fi – плотность распределения вероятности случайной величины 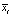 затрат ресурсов i-го вида.
затрат ресурсов i-го вида.
Использовать выражение (12) возможно, если известна аналитическая зависимость fi(ui) или правила позволяющие вычислить значение fi(ui), учитывающие влияние на fi характеристик процесса функционирования СТС. В рамках алгебры обобщенных рядов Грама – Шарлье построение зависимости fi не представляет ни теоретических, ни вычислительных проблем и подробно описана в [2].
Выводы
На основе анализа подходов к оценке эффективности предложен подход к оценке эффективности сложных технических систем с помощью обобщенных рядов Грама-Шарлье. Предложенный подход хорошо формализуем, минимизирует субъективность оценки эффективности присущие анализируемым подходам оценки эффективности. Он позволяет оценивать эффективность автоматических или автоматизированных, дискретных технологических систем, которые функционируют в условиях ограничений, наложенных на расходуемое количество ресурсов, с их пополнением или без их пополнения. При этом для его применения необходимо построение модели функционирования СТС в алгебре Грама – Шарлье.



