Типичная рыночная модель макроэкономики представляет собой систему трёх взаимодействующих открытых рынков: рынка производства товаров, рынка трудовых ресурсов и финансового рынка. Стационарные рынки описываются кривыми спроса и предложения, пересечения которых определяют точки динамического равновесия параметров экономической системы. Отклонения от равновесия любого из рынков в этой модели считаются малыми и обсуждаются обычно лишь качественно [1–3].
Для открытой неравновесной экономической системы необходимо совместное решение модели из трёх взаимозависимых дифференциальных уравнений, описывающих поведение производства товаров, трудовых ресурсов и финансов. Общее стохастическое поведение синергетической открытой трёхсекторной модели функционирования экономической системы как системы дифференциальных уравнений для основных параметров секторов экономики рассмотрено ранее [3]. Прогнозирование поведения социально-экономических систем с помощью детерминированных моделей представлено также в работах [2, 5].
Полагается, что субъекты в рыночной социально-экономической системе являются открытыми и неравновесными, обмениваются информацией и проводят финансовые операции. Обмен информацией и энтропией иногда приводит к понижению энтропии в системе, что ведёт к появлению новых минимумов функций Ляпунова системы, появлению новых структур и структурным изменениям с образованием новых форм в их организации и функционировании [2–5]. Целями феноменологической теории социально-экономических процессов является нахождение простейших моделей, описывающих данные системы и процессы в них. Эти модели могут восстанавливаться по динамическим рядам параметров исследуемых систем в виде регрессионных моделей. В динамических моделях проводится математический анализ возможных сценариев их поведения и выдача рекомендаций для оптимизации процессов управления. Задачи качественного анализа делают акцент на исследовании характерных черт всего явления, на прогнозировании явлений и управлении ими [2–6].
Синергетические модели процессов на финансовых рынках
Как во всякой нелинейной открытой экономической системе, в критических точках (катастрофы) может возникать поведение типа «динамический хаос» с последующей самоорганизацией новых оптимальных структур. Хаотическое поведение экономических параметров рынков вблизи точек экономических катастроф описывается в нелинейной динамике странными аттракторами [2–5]. Аттракторы в дальнейшем превращаются в другие формы самоорганизации: в циклические колебания экономических параметров, показывают стремление фазовых траекторий систем в устойчивые (неустойчивые) состояния типа циклов, узлов и фокусов. Математический анализ моделей проводится с помощью нелинейного анализа дифференциальных уравнений: бифуркационного анализа, теории катастроф [2–6].
Рассмотрим модель быстро релаксирующих рынков производства и трудовых ресурсов. Будем полагать, что медленно меняющимся со временем параметром является функция распределения капитала участников финансового рынка x(t). В этом случае в дифференциальном уравнении для распределения капитала параметры производства и трудовых ресурсов будут входить как квазиравновесные параметры. Исследуем проявление инновационной деятельности на свободных финансовых рынках с целью эффективного оптимального менеджмента. Зададим распределение финансовых инструментов, используемых участниками рынка для приращения капитала, функцией y(t), которая даёт удельную характеристику способов работы на рынке капитала. Функционирование финансового рынка осуществляется в некотором правовом законодательном поле, которое в уравнениях описываем как внешнее поле z(t), учитывающее влияние волатильного рынка валют, меняющиеся налоги и правила применения финансовых инструментов законодателями, Центробанком и т.д.
Запишем модель системы финансового сектора в виде дифференциальных уравнений для удельных параметров распределения: капитала x(t), финансовых инструментов y(t), используемых участниками рынка и внешнего поля условий функционирования z(t)
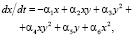(1)
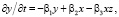
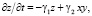
здесь α1х – непроизводственные расходы финансовой системы (личное потребление, социальные нужды), α3y2 – «зарабатывание» денег в структуре с эффективностью α3. Член α5y даёт вклад финансовых инструментов в приращение капитала, член α2xy – организация прироста капитала, требующая вложения средств с эффективностью α2, член α2xy2 даёт вклад капитала в планирование расходования средств на управленческую и исследовательскую деятельность с эффективностью α4, член α6x2 – учитывает корпоративное планирование и общую финансовую политику. Член β2x во втором уравнении системы (1) характеризует возрастание количества финансовых инструментов с ростом капитала, член β1y описывает изменение количества финансовых инструментов при их меняющейся эффективности, а член β3xz описывает влияние изменений капитала и поля внешних условий на распределение инструментов финансового рынка. Член γ1z в третьем уравнении системы (1) учитывает изменения в законодательстве и совершенствование налогов, член γ2xy характеризует влияние распределения капитала и финансовых инструментов на внешнее поле.
Наряду с эволюционным «гладким» поведением решения модели (1) существуют и области динамического хаоса в поведении её фазовой траектории. Действительно, при исчезающе малых коэффициентах модели α2, α3, α4, α6, α2 мы переходим к математической модели Лоренца [2, 3, 7]. Эта модель в наиболее простой и изученной форме описывает процессы самоорганизации систем, находящихся в хаотическом состоянии. Переходя к безразмерным параметрам в системе уравнений (1) приходим к стандартной математической модели Лоренца, представляющей собой три дифференциальных уравнения: для параметра порядка (ПП) η – капитал, сопряжённого ему поля h – финансовые инструменты и параметра внешних воздействий или управляющего параметра – S
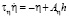, (2)
.
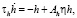
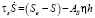Здесь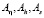 
– безразмерные константы связи, Se – стационарный, равновесный внешний управляющий параметр, 
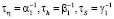– времена релаксации параметров модели. Исследуем динамику финансовой системы на основе модели (2) в области катастроф при переходе в хаотический режим. В этом состоянии фазовая траектория, описывающая поведение системы, переходит в режим «странного аттрактора», в котором её движение из-за непредсказуемости носит название «динамического хаоса».
Рассмотрим финансовый рынок в приближении синергетического подхода, учитывающего принцип подчинения всех степеней свободы выделенной – параметру порядка (ПП) η. При этом временная зависимость сопряжённого поля и внешних параметров определяется изменением ПП:
.
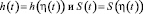Когда параметр внешнего воздействия S меньше критического значения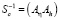 
, есть экстремум в точке 
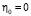и упорядочения в системе из динамического хаоса не происходит. В закритической области при S > Sc в минимуме функции Ляпунова система имеет ненулевой ПП
,
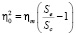где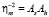 
и стационарное значение ПП растёт.
В закритическом режиме образуется область, притягивающая фазовые траектории. Система быстро движется к ней и при попадании в неё движение замедляется. Указанное множество соответствует эволюционному поведению системы. Так происходит переход от хаоса за счёт самоорганизации в новое устойчивое состояние [2, 4, 7].
В отсутствие сильного синергетического подчинения мод имеется область параметров αi, βi, γi, в которой возникают сложные квазипериодические движения, как решения системы (2) типа многомерного тора в фазовом пространстве, с аттрактором, называемым «странный аттрактор». В этой области параметров модели финансовая система демонстрирует поведение типа динамического хаоса, являющегося наиболее изученной и популярной математической моделью, демонстрирующей хаотическое поведение [2–5, 7].
Эволюционная динамика финансового рынка
В режиме динамического хаоса финансовый рынок характеризуется большой волатильностью курсов валют, акций и возможными скачкообразными изменениями этих и других параметров рынка вблизи экономических катастроф. В этих условиях наблюдается существенный рост энтропии информационных процессов с соответствующим сужением горизонта прогнозирования событий [2]. Непредсказуемость рынка ведёт к панике и дальнейшей турбулизации поведения финансовых систем. Что можно сделать, чтобы избежать хаотического поведения финансового сектора экономики?
Для перехода в новое квазистационарное состояние рынка необходимы стабилизирующие механизмы, переводящие систему в русло эволюционного развития. Для определения этих стабилизирующих механизмов рассмотрим более простую модель функционирования финансового сектора экономики (1), в которой будем полагать внешнее воздействие квазистационарным и его влияние на динамику процессов несущественным. Тогда математическая модель поведения финансового сектора может быть записана в виде
,
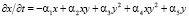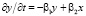. (3)
Коэффициенты αi, βi системы уравнений (3) в режиме плавной динамики определяют времена релаксации параметров x, y к квазиравновесным значениям, определяемым точками пересечения кривых спроса и предложения. Рассмотрим стационарные решения системы уравнений (3). Имеются два стационарных ненулевых решения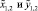 
, кроме тривиального решения 
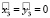. Анализ корней характеристического уравнения системы (3) показывает, что при условии
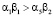(4)
в модели существует единственное положительное стационарное состояние равновесия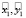 
. При выполнении условий для коэффициентов
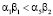и 
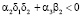(5)
в модели (3) таких равновесных положений два. Коэффициенты характеристического уравнения для системы уравнений (3) σ и Δ, получаемые при исследовании корней системы, определяют границы раздела на фазовой диаграмме неустойчивых решений типа седло, устойчивых и неустойчивых решений типа узел, седло и предельных циклов и имеют вид
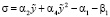, (6)
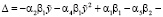
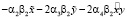. (7)
Соотношения (6), (7) показывают, что при Δ > 0 первое положительное стационарное состояние является: устойчивым фокусом или устойчивым фокусом без предельного цикла, который окружает неустойчивый предельный цикл; неустойчивым фокусом, вокруг которого есть единственный устойчивый предельный цикл; неустойчивым фокусом без цикла.
При Δ < 0 все решения системы (3) – неустойчивые решения типа седло.
Второе положительное состояние равновесия при выполнении условия (5) для Δ > 0 всегда устойчиво и предельных циклов не имеет.
Тривиальное равновесное положение может быть либо устойчивым фокусом, либо неустойчивым седлом.
Модели возникновения и банкротства банков
Рассмотрим поведение финансовых систем на основе модели (3) при малом коэффициенте α4, полагая связанные с ним нелинейные эффекты малыми. Можно показать, что в этой модели реализуются те же структуры, что и в модели (3), которая рассмотрена выше. Положения равновесия при этом имеют вид
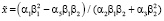, (8)
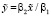. (9)
Коэффициенты характеристического уравнения σ и Δ имеют вид соотношений (6) и (7), в которых нужно положить α4 = 0. Показатель Ляпунова определяется соотношением
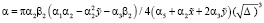. (10)
Можно показать, что урезанная математическая модель (3) сохранит структуру аттракторов модели (1) в фазовом пространстве. В состоянии равновесия (8), (9) имеется устойчивый фокус без цикла. Если фокус при определённых параметрах модели становится неустойчивым, то он имеет единственный предельный цикл. Этот цикл может стать неустойчивым при определённых параметрах. Равновесные положения (8), (9) могут быть неустойчивым фокусом без предельного цикла. Рассмотрим возможные режимы функционирования структур.
Отметим, что состояние равновесия (8) положительно при условии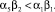 
Все рассмотренные структуры реализуются при условии, что положение равновесия является фокусом. Это условие режима накопления капитала участниками рынка. Обсуждённые ранее равновесные структуры могут быть устойчивыми, если они являются фокусами.
Фокус возникает при условии Δ > 0. Если при этом эффективность α1 возрастает, так что при этом Δ становится больше нуля, значительно возрастает накопление денег в финансовых структурах. Это ведёт к появлению новых структур, в том числе банков. Таким образом, банки появляются при бифуркации седла в фокус, и это условие является существенным для самого существования финансовых структур.
В моделях (1), (3) можно проследить за механизмом возникновения ростовщичества, то есть механизм обогащения финансовых структур за счёт вкладов под проценты. Он также возможен при накоплении значительного капитала и при бифуркации траектории от седла к фокусу. Если по каким-то причинам эффективность накопления α1 уменьшается, это может привести к изменению знака Δ (7) на отрицательный, что будет соответствовать переходу фокус –седло и переходу финансовой системы на неустойчивую траекторию. Для банковских систем это означает банкротство.
Модели возникновения финансовых корпораций
Реакцию на опасность возникновения неустойчивостей в финансовых рынках можно исследовать и на основе «полной» нелинейной математической модели (1). Линейные члены первого уравнения системы (1) дают скорости притока и оттока средств банковского капитала. Нелинейные члены α3y2 и α6x2 определяют вклады инновационной деятельности в финансовых структурах и вклад организационной и корпоративной деятельности объектов финансового рынка. При α4 = 0 равновесные точки модели определяются соотношениями
,
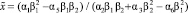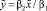. (11)
Коэффициенты характеристического уравнения получим следующие:
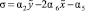, (12)
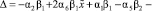
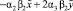. (13)
Наибольшее влияние на структуру и поведение финансовых систем имеет коэффициент эффективности накопления капитала. Если эффективность α1 начинает уменьшаться, то при α3 = α6 = 0 модель (1) может быть неустойчивой при достаточно малом значении α3α1 в коэффициенте Δ, определяемом соотношением (13). Он может стать отрицательным и произойдёт бифуркация в поведении системы от фокуса к седлу. При этом система становится неустойчивой, что ведёт к банкротствам финансовых структур. Но если в модели α3 ≠ 0 и α6 ≠ 0 и эффективности α3 и α6 достаточно значительны, может произойти обратная бифуркация от седла к фокусу с устойчивым эволюционным развитием финансовой системы. Практически увеличение эффективностей при нелинейных членах модели (1) может быть следствием некоторых коллективных (нелинейных) действий: либо в виде введения инноваций, например новых информационных технологий в банковской деятельности, либо в виде образования более крупных структур, корпораций. Крупные корпорации имеют большое значение в жизни финансовой системы, поскольку могут нести крупные затраты на венчурные проекты, проводить корпоративную политику стабилизации цен на рынке.
Заключение
Рассматриваемые математические модели (1–3) могут не только объяснить условия возникновения и банкротства финансовых структур, но и описать особенности поведения вблизи точек финансовых катастроф (бифуркаций). Наибольшее влияние на структуру и поведение финансовых систем имеют коэффициенты эффективности накопления капитала финансового рынка. Если коэффициенты эффективности начинают уменьшаться, происходит бифуркация в поведении системы от устойчивого эволюционного развития к неустойчивому, с возможным возникновением хаотического состояния, с сильно волатильным поведением параметров. Это ведёт к банкротствам финансовых структур. Благодаря моделированию появляется возможность прогнозирования и управления поведением структур рынка.
Получение конкретных оптимальных управленческих решений связано с верификацией моделей (1), (3), состоящей в нахождении констант систем уравнений по динамическим рядам параметров конкретных финансовых структур. Это позволит определить конкретное состояние, в котором находится финансовая система, построить динамическую модель эволюционного развития финансового рынка. Моделирование позволяет определять наличие опасных соседних областей, критических точек и принимать оптимальные управленческие решения, меняя условия функционирования моделей через их коэффициенты.