Электрогидравлический следящий привод нашёл широкое применение в различных областях техники, производств и технологических процессах. Это обусловлено высокой удельной мощностью привода по сравнению с пневматическими или электрическими приводами, возможностью позиционирования рабочего органа в промежуточных положениях с достаточной степенью точности и высоким быстродействием привода. Повышение точности отработки входных сигналов такими приводами является актуальной задачей. Решение данной проблемы напрямую связано с адекватностью математической модели привода реальному объекту. Однако при построении моделей таких приводов не учитываются характеристики питательного насоса и при составлении уравнения расходов рабочей жидкости, протекающей через гидравлический распределитель, принимается давление нагнетания постоянным.
Для повышения эффективности приводов широкое применение нашли автоматизированные питательные насосы с переменной производительностью с обратной связью по давлению. При использовании таких насосов давление нагнетания будет существенно зависеть от расхода рабочей жидкости, подаваемой потребителю и, как следствие, характеристика насоса будет оказывать существенное влияние на динамику привода.
При решении задач анализа и синтеза систем управления объектами различного класса широкое применение нашли проекционные методы, в основе которых лежит представление временных сигналов в виде конечного ряда Фурье в выбранном ортонормированном базисе. В результате можно перейти от рассмотрения временных сигналов к рассмотрению их спектральных характеристик, которые представляют собой множества коэффициентов Фурье рассматриваемого сигнала относительно выбранного базиса. Операции над сигналами заменяются операциями над векторами, что позволяет широко применять ЭВМ для решения задач управления. Теоретическое обоснование применения проекционных методов, их сходимость и эффективность отражены в соответствующей литературе, например в [3, 4].
Математическая модель привода с учётом характеристики насоса
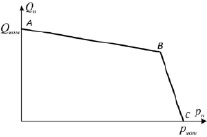
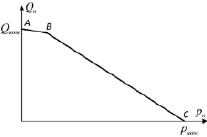
В современных гидравлических приводах в качестве источника энергии используются объёмные гидронасосы, основной характеристикой которых является зависимость расхода рабочей жидкости от давления в гидроприводе. График зависимости расхода от давления представлен на рис. 1 [1]. На рисунке Qном – номинальный расход гидронасоса при отсутствии нагрузки со стороны потребителя; pном – давление гидронасоса при нулевом расходе рабочей жидкости потребителю. Участок AB характеризует утечки рабочей жидкости в различных зазорах гидронасоса, а участок BC соответствует работе предохранительного клапана.
Очевидно, что при большой потребности рабочей жидкости давление нагнетания может снизиться до критических значений, при котором гидропривод не сможет развить достаточного усилия, обеспечивающего выполнение текущей операции. Для решения данной проблемы устанавливается гидравлический аккумулятор, который обеспечивает компенсацию пиковых расходов рабочей жидкости. Однако в некоторых гидроприводах, например, используемых в мобильных устройствах, в связи с высокими требованиями к массе или габаритам установка гидравлического аккумулятора нежелательна.
Зависимость давления нагнетания гидронасоса от расхода рабочей жидкости можно представить зависимостью
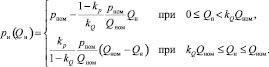 (1)
(1)
Здесь коэффициенты kQ и kp характеризуют жесткость расходных характеристик гидронасоса и предохранительного клапана соответственно. Введя обозначения
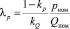 ,
,  , (2)
, (2)
последнюю систему уравнение можно переписать в виде
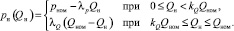 (3)
(3)
а) б)
Рис. 1. Расходно-перепадная характеристика гидронасоса: а) насос без управления; б) автоматизированный питательный насос
Расход рабочей жидкости через щель золотникового распределителя записывается уравнением [2, 5]
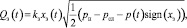 (4)
(4)
где рн – давление, развиваемое насосной станцией (давление питания); рсл – давление слива (обычно приравнивается нулю); xз(t) – перемещение золотника распределителя; kз – удельная проводимость окон золотникового распределителя, которое определяется зависимостью:
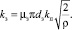
Здесь μз – коэффициент расхода окна, открываемого буртом золотника; dз – диаметр золотника; kп = bок/πdз – коэффициент полноты использования периметра втулки золотника окнами; bок – ширина окон; ρ – плотность рабочей жидкости.
Очевидно, что в (4) давление нагнетания рн зависит от расхода рабочей жидкости и определяется выражением (3). Расходы Qз и Qн связаны зависимостью
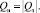
Знак расхода рабочей жидкости, протекающей через золотник, будет определяться знаком перемещения распределителя xз(t). Тогда
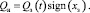 (5)
(5)
Таким образом, уравнения (3)–(5) определяют систему уравнений, решая которую относительно Qз получим уравнение расхода рабочей жидкости с учетом характеристики насоса, которое имеет вид
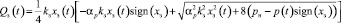 ,
,
при
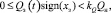 (6)
(6)
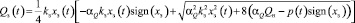 ,
,
при
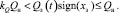 (7)
(7)
Как видно, в последних выражениях появляются дополнительные слагаемые, которые обусловлены характеристикой насоса, и чем сильнее смещается золотник распределителя от нейтрального положения, тем меньше будет расход рабочей жидкости, подаваемый потребителю, по сравнению со случаем, когда давление нагнетания насоса считается постоянным. Следовательно, скорость перемещения рабочего органа также будет отличаться от случая с постоянным давлением нагнетания насоса.
Модель электрогидравлического следящего привода с учётом характеристики насоса представляется системой уравнений (в данной модели динамика электрогидравлического усилителя не учитывается)
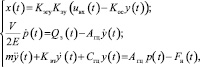
где Kэгу – коэффициент передачи ЭГУ; Kэу – коэффициент передачи электронного усилителя; Kос – коэффициент передачи датчика обратной связи по положению; V – объём полостей гидроцилиндра и подводящих трубопроводов; Е – модуль упругости рабочей жидкости; Aгц – площадь рабочей поверхности поршня; m – масса подвижных частей гидроцилиндра; Kвт – коэффициент вязкого трения подвижных частей гидроцилиндра (считается, что сухое трение отсутствует); Сгц – жесткость позиционной нагрузки гидроцилиндра; uвх(t) – входное напряжение; x(t) – перемещение плунжера золотникового распределителя; p(t) – перепад давления на поршне гидроцилиндра; y(t) – перемещение поршня гидроцилиндра; Fн(t) – внешняя нагрузка; Qз(t) – расход рабочей жидкости, протекающей через щели золотникового распределителя, определяемый зависимостями (6) и (7).
Таким образом, математическая модель привода, учитывающая характеристику насоса, является существенно нелинейной.
Анализ привода с использованием проекционного метода
Выполним линеаризацию уравнения расходов путём разложения в ряд Тейлора в окрестности рабочей точки с удержанием линейных слагаемых. В этом случае уравнение расхода рабочей жидкости, протекающей через щель распределителя, определяется уравнением
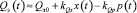 ,
,
где 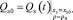 коэффициенты kQx и kQp с учётом (6) и (7) определяются из выражений
коэффициенты kQx и kQp с учётом (6) и (7) определяются из выражений
– при 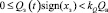 :
:
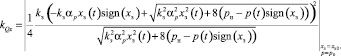 ,
,
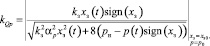 ; (8)
; (8)
– при 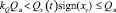 :
:
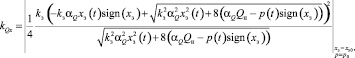 ,
,
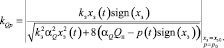 . (9)
. (9)
Очевидно, что значения коэффициентов линеаризации kQx и kQp отличаются для случая постоянства давления нагнетания насосной станции. Однако значения Qз0, kQx и kQp зависят от выбора x0 и p0.
В результате линеаризации система уравнений примет вид
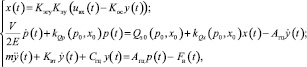
Выбрав некоторый ортонормированный базис Ф(t) и переходя к рассмотрению спектральных характеристик сигналов [3, 4], получим эквивалентную систему векторно-матричных уравнений
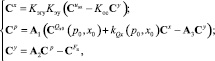 (10)
(10)
где A1 – матричный оператор, эквивалентный передаточной функции уравнения расходов 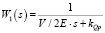 ; A2 – матричный оператор, эквивалентный передаточной функции уравнения движения поршня
; A2 – матричный оператор, эквивалентный передаточной функции уравнения движения поршня 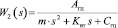 ; A3 – матричный оператор, эквивалентный передаточной функции местной обратной связи
; A3 – матричный оператор, эквивалентный передаточной функции местной обратной связи 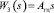 ;
;  , Cx, Cp, Cy,
, Cx, Cp, Cy, 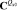 – спектральные характеристики сигналов uвх(t), x(t), p(t), y(t) и постоянной составляющей Qз0(p0, x0) в выбранном базисе.
– спектральные характеристики сигналов uвх(t), x(t), p(t), y(t) и постоянной составляющей Qз0(p0, x0) в выбранном базисе.
Очевидно, что решение полученной системы векторно-матричных уравнений зависит от выбранной точки линеаризации. Решать данную систему уравнений будем с применением метода последовательного приближения. Задав начальные значения давления 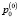 и величины открытия щели распределителя
и величины открытия щели распределителя 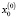 , находим значения коэффициентов линеаризации
, находим значения коэффициентов линеаризации 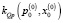 ,
, 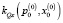 и постоянной составляющей
и постоянной составляющей 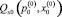 . Определив из (10) вектора Cx, Cp для начальных значений
. Определив из (10) вектора Cx, Cp для начальных значений 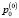 и
и 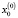 , а, следовательно, и сами сигналы x(t) и p(t), можно уточнить значения точки линеаризации, приняв за новые
, а, следовательно, и сами сигналы x(t) и p(t), можно уточнить значения точки линеаризации, приняв за новые
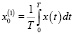 и
и 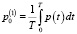 ,
,
где Т – интервал исследования.
Окончанием данного процесса является выполнение условий 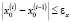 и
и 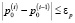 . Данный итерационный процесс будет сходящимся в силу устойчивости рассматриваемого объекта.
. Данный итерационный процесс будет сходящимся в силу устойчивости рассматриваемого объекта.
Ниже представлены результаты анализа привода с учётом характеристики насоса рассмотренным выше подходом использованием базиса блочно-импульсных функций и удержанием 256 элементов и для сравнения приведены графики моделирования исходных нелинейных моделей. При точности расчета по каждой координате, соответствующей 0,0001, за 5 итераций уточнены значения точки, в окрестностях которой выполняется представление нелинейного уравнения расходов в виде степенного ряда.
Заключение
В результате исследования построена математическая модель электрогидравлического следящего привода с учётом характеристики питательного насоса, которая оказывает влияние на динамику привода. Учёт характеристики насоса позволил получить адекватную модель привода и в то же время значительно её усложняет. Применение проекционных методов, позволяющих перейти от рассмотрения временных сигналов к их спектральным характеристикам, представляющим собой множество коэффициентов Фурье относительно выбранного базиса, дало возможность построить алгоритм анализа привода с учётом характеристики насоса, эффективность которого подтверждена результатами численного эксперимента. Рассмотренный подход в дальнейшем будет использоваться для решения задачи определения оптимальных числовых значений параметров привода из условия реализации на выходе процесса, максимально приближенного в известном смысле к заданному эталонному.
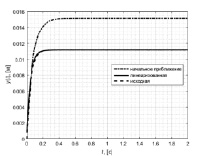 а)
а) 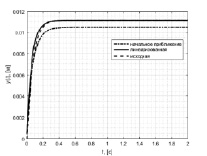 б)
б)
Рис. 2. Графики линеаризации модели ЭГСП с учётом характеристики управляемого насоса: а) без нагрузки; б) с нагрузкой, составляющей 75 % от максимально допустимой



