В современном проектировании конструкций и сооружений на основании со сложными инженерно-геологическими условиями при расчетах напряженно-деформированного состояния (НДС) большое мировое признание получило численное моделирование методом конечных элементов (МКЭ) [2, 5, 6]. На достоверность результатов численного моделирования влияет эффективная модель расчета, которая выбирается в зависимости от количества и достоверности характеристик грунтов. При этом если проблемы, связанные с применением программ для расчета напряженно-деформированного состояния общих геотехнических проблем, освещены достаточно подробно, то вопросы численного моделирования слабых оснований дорожных одежд автомобильных дорог, усиленных геоматериалами, изучены недостаточно.
Целью разработки расчетной модели являлось максимально достоверное описание процессов, возникающих в конструкции дорожных одежд автомобильных дорог.
В большинстве случаев для исследования НДС оснований применяется математический аппарат теории упругости. Для задач с пошаговым приложением нагрузки, особенностью которых является смена направления главных напряжений в процессе нагружения, наилучшие результаты получены для упругопластичной модели, вычисляемой по теории пластического течения [1]. Этими преимуществами и определяется использование в работе данной модели.
Предлагаемая методика численного моделирования работы конструкций основания дорожной одежды автомобильных дорог, усиленных геоматериалами, является составной частью модульной программы FEM Models. Данная программа осуществляет упругопластическое решение методом конечных элементов (МКЭ) с использованием процедуры «начальных напряжений». Базовой программой является «Геомеханика» [6], по которой подбираются интерполирующие полиномы и строится матрица жесткости конечного элемента, в узлах которых составляются и решаются системы алгебраических уравнений.
Деформация грунта представлена в виде суммы упругих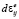 
и пластических 
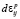деформаций
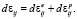(1)
Для определения dεij применяется теория пластического течения в форме неассоциированного закона:
, 
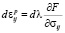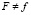, (2)
где dλ – малый скалярный множитель; F – пластический потенциал; σij – компоненты напряжений; f – критерий предельного состояния.
Когда вектор напряжения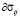 
проходит из упругого состояния в пластическое через плоскость, близкую к поверхности предельного состояния, на которой находится конец вектора, то происходит нейтральное нагружение, где образуются только упругие деформации. Это является условием непрерывности [3].
В решении упругопластической задачи, где возникает плоская деформация, применяется схема пластической среды с критерием прочности Кулона в виде
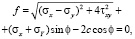(3)
где σx, σy; τxy – напряжения в осях; ϕ – угол внутреннего трения; c – удельное сцепление. Численная реализация упругопластической модели слоистых оснований
Реализация модели грунтовой конструкции основания осуществляется следующим образом.
Если напряжение в грунте меньше предельного, при влиянии внешних нагрузок, где связь между напряжениями и деформациями описывается законом Гука (область I, рис. 1), который для условий плоской деформации может быть выражен как
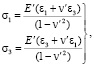(4)
где 
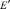и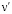 
– плоские аналоги модуля Юнга и коэффициента Пуассона.
Область I ограничена напряжением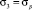 
в зоне растяжения, а в области сжатия – критерием прочности Кулона.
Относительные деформации определяются с использованием уравнений Коши (5), а упругие напряжения по закону Гука, которые суммируются с ранее накопленными.
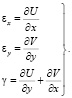(5)
Следующим этапом происходит вычисление главных суммарных напряжений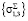 
и их направления по формулам поворота осей:
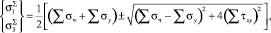(6)
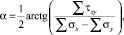(7)
где α – угол между σ1 и осью х.
Затем происходит сравнение главных суммарных напряжений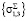 
с границами текучести:
Если точка главных напряжений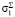 
, 
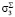, попадает в область упругости I, то конечный элемент находится в упругом состоянии и корректировке напряжений не подлежит.
Если точка суммарных напряжений MII попадает в основную зону пластичности (область II), то точка теоретических напряжений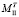 
лежит на пересечении границы текучести и прямой 
.
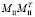Если точка MIII попадает в зону III, то теоретические напряжения примут значения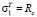 
, 
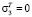. Это значит, что напряжения σ1 снизятся до уровня сопротивления грунта на одноосное сжатие и конечный элемент, в направлении действия напряжения σ3, будет разорван.
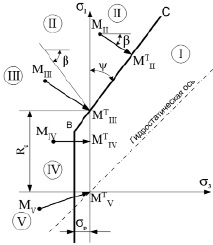
Рис. 1. Схема определения в упругопластической модели грунта теоретических напряжений
Рис. 2. Лоток и оборудование для штамповых испытаний: 1 – прогибомер 6-ПАО; 2 – реперная балка; 3 – гидравлический цилиндр; 4 – штамп; 5 – маслонасосная станция; 6 – манометр
В области IV напряжения σ1 не превосходят сопротивление одноосному сжатию,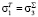 
, 
.
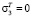В области V конечный элемент будет разорван по всем направлениям,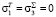 
.
Модель учитывает природное напряженное состояние массива грунтового основания по основным характеристикам свойств в механике грунтов (Е, ν, γ, с, φ, IL). Данные характеристики определяются по стандартным методикам Российской Федерации. Это является преимуществом используемой грунтовой модели.
С использованием данной модели было выполнено моделирование напряженно-деформированного состояния конструкции в выполненных лабораторных испытаниях на полигоне Лаборатории механики грунтов ДВГУПС [4, 7], методом испытания грунтов круглым штампом по ГОСТ 20276-2011, с возможностью измерения напряжений в грунте (рис. 2).
Напряжения в грунте фиксировались с помощью двух месдоз марки BEC-A-1MP компании KYOWA Electronic Instruments (Япония).
Моделирование лабораторных испытаний
В программном комплексе FEM Models построена модель лабораторных штамповых испытаний. Расчетная схема модели представляет слоистую систему грунтового основания внутри лабораторного лотка с круглым жестким штампом, диаметром 300 мм, и вертикальной нагрузкой на штамп 56 кН. Расчетная схема представлена на рис. 3.
По результатам численного моделирования получены данные:
1. Осадка штампа под нагрузкой 56 кН составляет 4,1 мм для неармированной конструкции, 2,9 мм – для армированной.
2. Вертикальные напряжения в месте расположения датчика вертикального давления под штампом составляют: 357 кПа для неармированной конструкции, 262 кПа – для армированной.
Изолинии вертикальных напряжений представлены на рис. 4.
3. Горизонтальные напряжения в месте расположения датчика горизонтального давления составляют: 138 кПа для армированной конструкции, 95 кПа – для неармированной.
Изолинии горизонтальных перемещений без армирования и с армированием представлены на рис. 5.
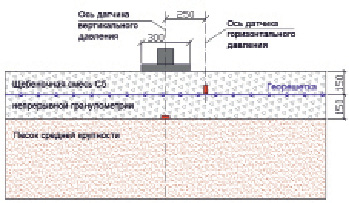
Рис. 3. Расчетная схема армированной конструкции
Рис. 4. Изолинии вертикальных напряжений армированной конструкции (напряжение в кПа)
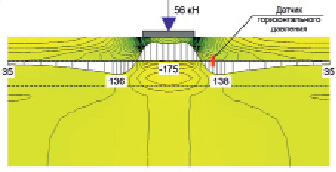
Рис. 5. Изолинии горизонтальных напряжений армированной конструкции (напряжение в кПа)
Выводы
1. Экспериментальные исследования показали эффективную работу георешетки в основании дорожной одежды, где за счет мембранного эффекта армирующего материала происходит уменьшение деформации из-за распределения напряжений, а за счет эффекта блокировки – значительно увеличивается сдвигоустойчивость конструкции.
2. Разработана методика расчетного обоснования взаимодействия георешетки в основании конструкции дорожных одежд автомобильных дорог, которая учитывает параметры их совместной работы.
3. По результатам численного моделирования лотковых испытаний были получены напряжения в местах расположения датчиков вертикального и горизонтального давлений, разница которых не превышает 10 % от фактических. Это свидетельствует об эффективности метода расчета МКЭ, при моделировании армированного слоя щебня в основании дорожных одежд с эквивалентным модулем упругости.
4. После сопоставления лабораторных и численных испытаний было проведено моделирование других вариантов сочетаний конструктивных слоев, в ходе которого подтвержден коэффициент усиления (армирования), для георешетки и слоя щебня толщиной 15 см, равный 3,5.